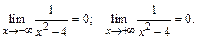Число 
называется пределом функции 
при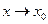 
, если для любого сколь угодно малого 
найдется 
, такое что для всех значений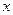 
, удовлетворяющих неравенству 
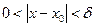, выполнено неравенство 
.
При этом пишут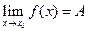 
или 
. В символах математического анализа определение может быть записано так:
.
Выше приведено определение для случая конечных значений и 
. Оно может быть переделано для случаев, когда или обращаются в бесконечность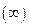 
. При этом соответствующие неравенства должны быть заменены на неравенства типа 
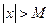, если 
, 
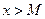,если 
, 
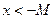, если 
и т.п.
Переменная величина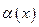 
называется бесконечно малой величиной при 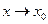, если 
.
Пусть 
, где 
– конечные числа, 
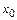– любое конечное число или бесконечность.
Теоремы о пределах:
1. 
.
2. 
.
3. Если 
.
4. Пусть 
– конечное число. Тогда:
а) 
б)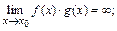 
в)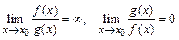 
.
5. Пусть 
, тогда 
. ●
Функция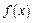 
называется непрерывной в точке 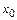, если она определена в этой точке и 
. Для непрерывной функции возможен переход к пределу под знаком функции.
Предельные переходы, содержащие нуль или бесконечность, при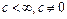 
кратко можно записать так:
, (1)
где выражение, заключенное в квадратные скобки, понимается как предельное значение. Выражения вида:
, (2)
─ называются неопределенностями, что означает, что нельзя дать ответ, используя правила (1), Например, рассмотрим три функции: 
при 
. Отношение любых двух функций из указанных трех приводит к неопределенности 
. Однако, пределы этих отношений различны, например:
, 
, 
.
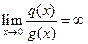Неопределенности (2) всегда можно перевести из одной в другую. Кроме указанных выражений неопределенностями являются предельные выражения:
.
При вычислении пределов сначала подставляется предельное значение переменной. Если выполнены условия теорем, то сразу получаем ответ. Если при подстановке получается неопределенность, то следует предварительно преобразовать выражение, а затем подставить предельное значение.
Рассмотрим несколько примеров на вычисление пределов.
1. 
.
2. 
.
3. 
.
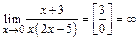4. 
.
5. 
.
6. 
.
7. 
.
8. 
.
9. 
.
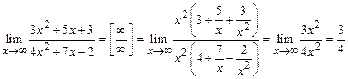10. 
.
11. 
.
12. 
.
13. 
В примерах 1─3,6─8 можно сразу записать ответ. В остальных примерах первая подстановка приводит к неопределенности, поэтому: сначала проводим преобразование. Так в примере 13 мы умножили числитель и знаменатель на сопряженное выражение, что позволило затем сократить дробь. Обратите внимание, что выражение 
, и это позволило вынести множитель 
за знак предела.
Проанализировав решения примеров 9–11, замечаем, что при вычислении пределов типа 
, приходим к пределу отношения членов со старшими степенями. Окончательный ответ зависит от соотношения степеней. Аналогичная ситуация и для выражений, содержащих дробные степени или радикалы.
Например, вычисляя 
, приходим к неопределенности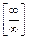 
. Выбрав в числителе и знаменателе слагаемые со старшими степенями 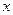. получаем решение:
.
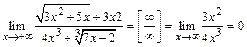Односторонние пределы
Если 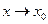, оставаясь больше (или меньше) , то такие пределы называются односторонними пределами или пределами справа (слева). Стремление переменной к предельному значению слева будем записывать 
при стремлении справа 
, а сами предельные значения функции 
или 
. При или также имеем односторонние пределы: 
и 
. Сравните два предела
, 
.
Как указано в первом разделе: функция 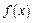называется непрерывной в точке 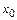, если она определена в этой точке и . Если функция не является непрерывной в точке , то говорят, что функция имеет разрыв в точке . Разрывы функции имеют три типа и связаны с поведением функции слева и справа от точки разрыва.
1. Устранимый разрыв. Существуют левосторонний и правосторонний пределы, оба предела конечны, равны между собой, а функция не определена в точке :
.
2. Разрыв первого рода (скачок). Существуют левосторонний и правосторонний пределы, оба предела конечны, но они не равны между собой.
3. Разрыв второго рода. Один из пределов или оба обращаются в бесконечность или не существуют.
Все элементарные функции непрерывны в области своего определения.
Пример 1. Исследовать поведение функции 
на границе ее области определения.
Решение. 
.
Определим пределы функции в граничных точках 
и при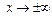 
:
Пример 2. Исследовать поведение функции 
на границе ее области определения.
Решение.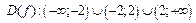 
.
Определим пределы функции в граничных точках 
и при 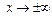. Заметим, что каждая из точек 
граничной точкой является дважды. Поэтому в этих точках вычислим односторонние пределы:
