ЗАЦЕПЛЕНИЯ
1. Коэффициент перекрытия ea.
Характеризует плавность работы зубчатой передачи и показывает, какое число зубьев одновременно участвуют в перекрытии зацепления (насколько одна пара зубьев перекрывает работу другой). Теоретически может ea = 1, и это означает, что как только одна пара зубьев вышла из зацепления, следующая пара сразу же вошла в зацепление. Если ea <1, то предыдущая пара зубьев из зацепления вышла, а следующая пара в зацепление не вошла. Такая передача работает с ударами, и ее применение недопустимо. Поэтому конструкторы при проектировании передачи считают минимально допустимым e a равным 1,05. Как правило, эвольвентная зубчатая передача с прямозубыми колесами имеет коэффициент перекрытия ea =1,1 – 1,5.
Для косозубых колес за счет осевого перекрытия зубьев eb = ea + g, eg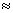 
1 = > e b =2,1 – 2,5. Зубчатая передача с косозубыми колесами работает более плавно.
Имеются несколько вариантов определения коэффициента перекрытия ea :
а) Определение коэффициента перекрытия по линейным параметрам.
или 
где
ga - длину зацепления, ga = АВ,
ra - шаг зацепления по основной окружности,
r - шаг зацепления по делительной окружности.
По замеренным из чертежа величинам ga и ra можно подсчитать значение коэффициента торцового перекрытия.
б). Определение коэффициента перекрытия по угловым параметрам.
или 
где
и 
- углы торцового перекрытия;
t1 и t2 - угловые шаги колес.
Коэффициент торцевого перекрытия εα – это отношение угла торцевого перекрытия φα зубчатого колеса цилиндрической передачи к его угловому шагу τ = 360/ z. Этот коэффициент характеризует плавность работы зацепления. С уменьшением εα (особенно до величины, меньшей 1,2) возрастают колебания угловых скоростей зубчатых колес, а следовательно, и дополнительные динамические нагрузки. Поэтому коэффициент торцевого перекрытия косвенно влияет на нагрузочную способность передачи. Уменьшение его до εα < 1,2 нежелательно, хотя передача будет работать при предельном значении εα = 1.
Коэффициент торцевого перекрытия может быть определен по формуле
(1)
Значения углов αа1 и αа2 определяются соответственно тригонометрическими функциями:
и 
.
Если предварительно вычислить разности А 1 = tg α1 – tg αw, A2 = tg α2 – tg αw,
то формулу (1) можно записать так
Аналогично сокращаются записи формул вычисления наибольших
удельных скольжений.
Для рассматриваемого примера
А 1 = tg α1 – tg αw = 0,7015 – 0,5012 = 0,2003,
А 2 = tg α2 – tg αw = 0,6924 – 0,5012 = 0,1912,
Если значение εα значительно отличается от величины, принятой при выборе x1 и x2 по блокирующему контуру (более чем на 0,01), то допущена ошибка в расчётах или при определении коэффициентов смещений; её необходимо устранить.
2. Коэффициент удельного давления n.
Характеризует прочностные характеристики передачи с точки зрения контактных напряжений в высшей КП.
Коэффициент повышения контактной прочности показывает приблизительно (теоретически), во сколько раз контактная прочность передачи, имеющей угол зацепления α w, выше по сравнению с передачей, у которой α w = 20°, при прочих равных параметрах (модулях, числах зубьев колес и др.).
Смысл этого показателя становится яснее, если вспомнить, что с увеличением угла зацепления возрастают радиусы кривизны рабочих поверхностей зубьев, а следовательно, и допустимая нагрузка на зубья.
3. Коэффициент удельного скольжения l.
Характеризует износостойкость зубчатой передачи в высшей КП.
Удельное скольжение в контактной точке профиля зуба –
это отношение скорости скольжения зубьев к скорости перемещения контактной точки по профилю зуба данного зубчатого колеса. От его значения зависит износостойкость зубьев и стойкость их против заедания рабочих поверхностей зубьев, которые возрастают по мере уменьшения удельного скольжения. Удельное скольжение переменно вдоль профиля зуба и достигает максимума в одной из крайних точек активного профиля зуба. В полюсе
зацепления оно равно нулю.
Наибольших значений удельные скольжения достигают обычно на ножках зубьев (в нижних точках активных профилей).
Для рассматриваемой передачи они равны:
– у шестерни:
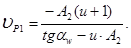
– у колеса:
Наибольшее значение удельных скольжений на головках зубьев (в верхних точках активных профилей):
– у шестерни:
– у колеса:
4. Коэффициент формы зуба Y.
Коэффициент формы зуба Y характеризует соотношение высоты зуба и его толщины у основания. От величины Y зависит прочность зуба на излом. Чем больше Y, тем большую нагрузку может выдержать зуб. Формулы для вычисления коэффициента формы зуба и исследования приводятся в курс «Детали машин и основы конструирования».
Результаты расчетов примера
