Геометрия эвольвентного зубчатого колеса

Рис.1. Схема принципа образования эвольвенты

Рис.1. Схема для пояснения инвалюты эвольвенты - inv α
Параметры эвольвенты и зависимости между ними.
Угол развернутости эвольвенты между нормалями к эвольвент е в ее предельной, принадлежащей основной окружности, и рассматриваемой точках:

Учитывая, что дуга АоМ = АМ
так как прямая перекатывается по окружности без скольжения, а
AM = rb tgα, получаем:
где α – профильный угол эвольвенты, т.е. угол между текущим радиус-вектором ОА и касательной KK к эвольвенте в точке А, равный углу между радиус-вектором ОА и радиусом ОМ основной окружности, проведенным в точку М касания производящей прямой.
Радиус кривизны эвольвенты:
ρ = AM = rb tgα.
Текущий радиус-вектор точки эвольвенты:
ri = OA = rb / cos α
Полярный угол эвольвенты, или эвольвентный угол, определяющий
направление текущего радиус-вектора:
θ = υ − α = tgα – α = inv α.
Полученную функцию угла α называют эвольвентной функцией,
или инволютой, и используют ее при геометрическом расчете эвольвентных профилей. Значения invα в табличной форме приведены в специальной литературе.

Рис.3. Геометрические параметры цилиндрического прямозубого зубчатого колеса внешнего зацепления с эвольвентным профилем
π = 3,141593. 1o = 0,017453 радиан. 1 рад. = 57,2957795 o = 57 o 18ʹ
α = 20o = 0,349066 рад. cos 20o = 0,939693; tan 20o = 0,363970;
1. Модудь m = p/π. Стандартизирован ГОСТ 9563-60 (СТ СЭВ 310-76)
2. Диаметр делительный d = m ∙ z; (r = m ∙ z / 2).
3. Диаметр основной окружности db = d ∙ cos α
4. Окружность вершин.
4.1. Диаметр окружности вершин da = d + 2∙ ha = d + 2∙ ha* ∙ m.
4.2. Определить радиусы вершин зубьев. В передаче без смещения коэффициенты смещения и уравнительного смещения равны нулю, поэтому
ra 1 = r 1 + ha ∙ m, мм;
ra 2 = r 2 + ha ∙ m, мм.
5. Диаметр окружности впадин df = d - 2∙ hf = d + 2∙ hf* ∙ m.
6. Диаметр начальной окружности
7. Высота зуба h = ha + hf
8. Высота головки зуба ha = ha* ∙ m = 1 ∙ m.
(ha* = 1,0 для нормального зуба; ha* = 0,8 для укороченного зуба).
9. Высота ножки зуба hf = hf* ∙ m = 1 ∙ m.
(hf* = 1,25 для нормального зуба; hf* = 1,0 для укороченного зуба).
10. Шаг зубьев (шаг зацепления) p = m ∙ π; p = s + e.
11. Толщина зуба по делительной окружности s = p/2 = m ∙ π /2.
12. Ширина впадины по делительной окружности e = p/2 = m ∙ π /2.
13. Угловой шаг τ = 360о / z градусов или τ = 2π / z радиан.
РАСЧЕТ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
ЦИЛИНДРИЧЕСКОЙ ЭВОЛЬВЕНТНОЙ ПЕРЕДАЧИ ВНЕШНЕГО
ЗАЦЕПЛЕНИЯ
Рассмотрим методику расчета на примере зубчатой передачи наибольшей прочности по излому зубьев (НИ), z1 = 17, z2 = 22, модуль
m = 10 мм. Ведущее колесо 2.
Параметры исходной производящей рейки (по ГОСТ 13755-68): угол
профиля α = 20°; коэффициент высоты головки ha * =1; коэффициент радиального зазора с * = 0,25.
В соответствии с прочностными требованиями по блокирующему
контуру для чисел зубьев 17, 22 (прил.1) определяем коэффициенты смещения как координаты точки пересечения линии εα = 1,2 с линией б-б (ведущим является колесо), x 1 = 0,42, x 2 = 0,74.
Последующие расчеты являются общими и для передач с другими
прочностными и качественными характеристиками.
Все расчеты геометрических параметров необходимо выполнять
тщательно, при проверках добиваться совпадения результатов с точностью
до двух десятичных знаков.
1. Коэффициент суммы смещения:
x Σ = x 1 + x 2 = 0,42 + 0,74 = 1,16.
x 1 и x 2– величины алгебраические.
2. Угол зацепления:
inv α w = 2 x Σ tg α /(Z1+ Z2) + inv α =2 ∙1,16∙ 0,3640/(17 + 22)+ 0,01490 =0,03655.
По эвольвентной функции (прил.3) определяем
α w = 26,45°.
Расчет величины inv α w необходимо делать с точностью до шестого
десятичного знака и округлять до пятого знака. Угол зацепления определяется с точностью до одной минуты.
3. Межосевое расстояние:
 мм.
мм.
Значение косинусов и их отношение определяют с точностью до четырех десятичных знаков, aw и последующие линейные величины вычисляют в миллиметрах с точностью до второго десятичного знака.
4. Делительное межосевое расстояние:
 мм.
мм.
5. Делительные радиусы:
 мм и
мм и  мм.
мм.
6. Основные радиусы:
r b1 = r 1 ∙ cos α = 85⋅0,9397 = 79,87 мм;
r b2 = r 2 ∙ cos α = 110⋅0,9397 = 103,37 мм.
7. Передаточное число:  .
.
8. Начальные радиусы:
 мм;
мм;
 мм.
мм.
Проверяем: aw = rw 1 + rw 2 = 89,50 + 115,45 = 204,95 мм.
9. Коэффициент воспринимаемого смещения – отношение воспринимаемого смещения к модулю:

Значение у подсчитывают с точностью до трех знаков.
Проверяем: aw = a + ym = 195 + 0,995⋅10 = 204,95 мм.
10. Коэффициент уравнительного смещения:
Δ у = х Σ – у = 1,16 – 0,995 = 0,165.
11. Радиусы вершин зубьев:
r a1 = r 1 + (ha *+ x 1 – Δ у) m = 85 + (1 + 0,42 – 0,165)10 = 97,55 мм;
r a2 = r 2 + (ha *+ x 2 – Δ у) m = 110 + (1 + 0,74 – 0,165)10 = 125,75 мм.
12. Радиусы впадин:
rf 1 = r 1 – (ha *+ c * – x 1) m = 85 – (1 + 0,25 – 0,42)10 = 76,70 мм;
rf 2 = r 2 – (ha *+ c * – x 2) m = 110 – (1 + 0,25 – 0,74)10 = 104,90 мм.
13. Высоты зубьев:
h 1= ra 1 – rf 1 = 97,55 − 76,70 = 20,85мм;
h 2= ra 2 − rf 2 =125,75 −104,90 = 20,85мм.
Проверяем: h 1 = h 2 = 20, 85 мм.
14. Толщина зубьев:
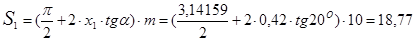 мм,
мм,
 мм.
мм.
15. Шаг зубьев (по делительной окружности):
p = π⋅ m = 3,1415⋅10 = 31,42 мм.
16. Шаг зацепления (по начальной окружности):
pw = p b= π⋅ m ⋅cos α = 3,1415⋅10⋅0,9390 = 29,50 мм.
РАСЧЕТ КАЧЕСТВЕННЫХ ХАРАКТЕРИСТИК






