Очень часто потоки в промышленных аппаратах не соответствуют ни идеальному вытеснению, ни идеальному смешению. По гидродинамической структуре потоков их относят к аппаратам промежуточного типа. В таких случаях игнорирование действительных полей скоростей, температур и концентраций и использование идеализированных представлений о структуре потоков может привести к большим ошибкам при расчетах промышленных аппаратов. Кривая отклика для аппаратов промежуточного типа может существенно отличаться от кривых отклика для МИВ и МИС (рис. 5-5). Введенный импульсом индикатор в выходящем потоке сначала не обнаруживается. К моменту τ1 выходного сечения достигает наиболее быстрая часть потока, и индикатор появляется. Затем концентрация индикатора возрастает до момента τ2, а потом начинает убывать, так как основная масса потока прошла, и выходят те доли объема индикатора, которые попали в зоны застоя или циркуляции. Выход этой части индикатора обычно продолжается длительное время.
Для идеализированных моделей расчет скоростей процессов и размеров соответствующих аппаратов при известных кинетических коэффициентах достаточно хорошо разработан (например, расчет поверхности теплопередачи теплообменников). Значительно труднее описать и учесть реальное поле температур или концентраций при расчете аппаратов промежуточного типа. В этих аппаратах возникает градиент температур или концентраций по длине аппарата, так как обратное перемешивание неэквивалентно идеальному перемешиванию.
Наибольшее распространение среди промежуточных моделей получили однопараметрические модели - ячеечная и диффузионная. Ячеечная модель схематически представляет собой реальный аппарат как некоторое число п одинаковых последовательно соединенных аппаратов (ячеек) идеального смешения (рис. 6). Суммарный объем всех ячеек равен объему реального аппарата. Следовательно, объем одной ячейки (при условии равенства их объемов)  Параметром, характеризующим данную модель, является число ячеек n.
Параметром, характеризующим данную модель, является число ячеек n.
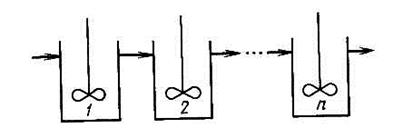
Рис. 6. К пояснению ячеечной модели структуры потоков
Математическое описание ячеечной модели включает n линейных дифференциальных уравнений первого порядка
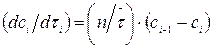

Дифференциальная функция распределения времени пребывания [кривая отклика с (θ)]
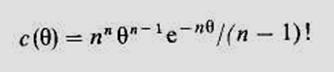
График этой функции для различных n представлен на рис. 7.
При n →∞ со ячеечная модель переходит в МИВ; при n = 1 ячеечная модель переходит в МИС, а уравнение (13)-в уравнение (10).
Таким образом, МИВ и МИС являются крайними случаями ячеечной модели.
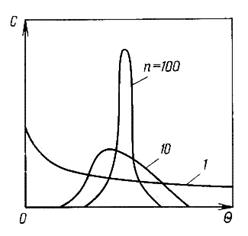
Рис. 7. Кривые отклика для ячеечной модели при импульсном вводе индикатора
Из уравнения (13) можно вывести простую зависимость для дисперсии:


Уравнением (14) удобно пользоваться для определения числа ячеек.
Диффузионная модель. Основой этой модели является модель идеального вытеснения, осложненная обратным перемешиванием, наличие которого описывается формальным законом диффузии, т. е. к уравнению (8) добавляется диффузионный член, учитывающий турбулентную диффузию или перемешивание (DL- коэффициент продольной диффузии, учитывающий и молекулярную, и турбулентную диффузию, а также неравномерность поля скоростей). В практических задачах DL обычно является эмпирическим параметром. Причем считается, что DL постоянен по длине аппарата.
Таким образом, единственным параметром этой модели является коэффициент продольной диффузии DL (или коэффициент продольного перемешивания). Но при одном и том же значении DL картина перемешивания может быть разной - на нее влияют также длина аппарата и скорость потока. Поэтому, чтобы распространить результаты на ряд подобных процессов, продольное перемешивание характеризуют критерием подобия Пекле
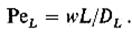
Анализ уравнения (16) показывает, что при PeL = 0 (DL = ∞) поток соответствует идеальному смешению (бесконечно быстрая диффузия полностью выравнивает концентрации). При PeL=∞ уравнение (15) переходит в уравнение (8) – поток движется по схеме идеального вытеснения. Реальному же потоку соответствуют условия 0 < PeL < ∞.
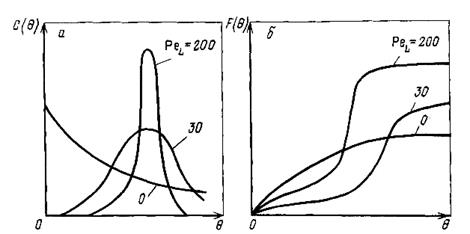
Рис.8. Кривые отклика для диффузионной модели при импульсном (а) и ступенчатом (б) вводе индикатора
Кривые отклика диффузионной модели при ступенчатом и импульсном возмущении показаны на рис. 8.
Дисперсию времени пребывания можно рассчитать по формуле:
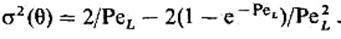
При PeL > 10, т. е. когда реальный поток незначительно отклоняется от идеального вытеснения, справедлива приближенная формула

С учетом (14) получим соотношение
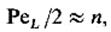
устанавливающее соответствие между ячеечной и диффузионной моделями.
Диффузионную модель обычно используют для описания структуры потоков в аппаратах с непрерывным контактом фаз (например, в насадочных и пленочных массообменных колоннах и т.п.).
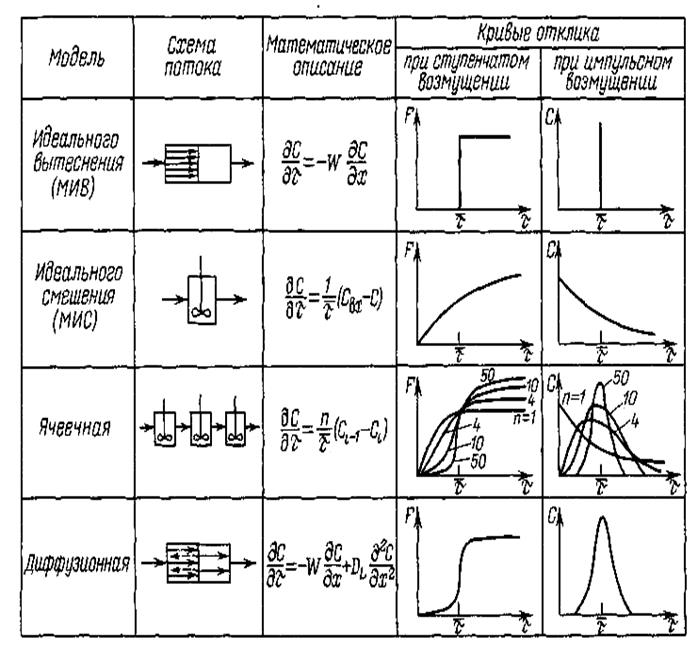
В табл.1. представлены схемы потоков, соответствующие рассмотренным моделям, их математическое описание и кривые отклика.
Кроме однопараметрической диффузионной модели достаточно широко используют двухпараметрическую диффузионную модель, учитывающую перемешивание как в продольном, так и в поперечном направлениях. Эта модель характеризуется коэффициентами продольного (DL) и радиального (Dr) перемешивания:
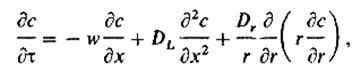
где r -радиус. Коэффициенты радиального перемешивания Dr и продольного перемешивания DL определяют опытным путем.
Схемы потоков, математическое описание их моделей и кривые отклика
Комбинированные модели.
Не все реальные процессы удается описать с помощью рассмотренных выше моделей-в частности, процессы, в которых наблюдаются байпасные и циркуляционные потоки, застойные зоны. В таких случаях используют комбинированные модели структуры потоков. При построении такой модели принимают, что аппарат состоит из отдельных зон, соединенных последовательно или параллельно, с различными структурами по-I токов (идеального вытеснения, идеального смешения, зона с продольным перемешиванием, застойная зона и т.д.). Например, аппарат, в котором имеются короткий байпас и зона циркуляции, можно изобразить схемой, показанной на рис. 9. Основная часть потока Q1 движется по схеме диффузионной модели (параметр которой PeL) через часть аппарата объемом Va1. Часть потока Q2 попадает в зону циркуляции объемов Va2 с практически идеальным перемешиванием. Часть потока Q3 по схеме идеального вытеснения идет коротким байпасом, занимая объем Va3.
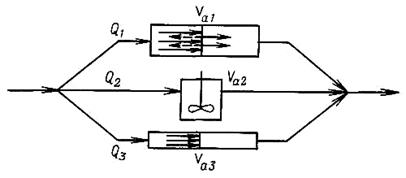
Рис. 9. Схема комбинированной модели структуры потоков:
Va1,-аппарат, работающий в режиме диффузионной модели, Va2-аппарат идеального смешения; Va3-аппарат идеального вытеснения
В рассмотренной модели пять параметров: доли потоков Q1/Q2 и Q2/Q (долю Q3/Q находят по разности (1 – (Q1/Q2 + Q2/Q) = Q3/Q); доли аппарата Val/V и Va2/V; параметр PeL. Столь сложные модели требуют тщательной оценки параметров во избежание ошибочных заключений о степени их влияния на структуру потока.
Следует иметь в виду, что увеличением числа зон различных структур потоков можно описать процесс любой сложности, но математическое моделирование при этом усложняется. Их описание приводится в специальной литературе.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. В чем проявляется влияние гидродинамической структуры потоков на химико-технологические процессы?
2. Что понимают под средним временем пребывания частиц потока в аппарате, от чего оно зависит и как определяется?
3. Сопоставьте идеализированные модели структуры потоков МИВ и МИС. Какой вид кривых отклика для этих моделей? Назовите примеры аппаратов, в которых гидродинамическая структура потоков близка к МИВ и МИС.
4. Охарактеризуйте ячеечную и диффузионную модели структуры потоков. При каких условиях с помощью этих моделей можно принимать, что тот или иной аппарат близок по гидродинамической структуре к МИВ или МИС?






