Матрицы. Действия над матрицами.
Матрицей называется множество чисел или других математических объектов, образующих прямоугольную таблицу, которая содержит m строк и n столбцов. Объекты, входящие в таблицу, называются элементами матрицы.
Обозначения матрицы:
; 
; 
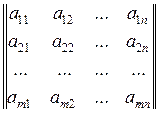
Для любого элемента 
первый индекс i означает номер строки, а второй, j,- номер столбца, где расположен элемент.
Матрицу, имеющую m строк и n столбцов, называют матрицей размеров m 
n.
Употребляются краткие обозначения матрицы размеров m n:
; 
; 
.
Матрицы также обозначаются латинскими заглавными буквами: A, B, C …
Если число строк не равно числу столбцов, то матрица называется прямоугольной.
Например: 
Если число строк равно числу столбцов, то матрица называется квадратной:
.
Число строк или столбцов квадратной матрицы называется её порядком.
Диагональ квадратной матрицы, содержащая элементы 
, называется главной, а диагональ, содержащая элементы 
, – побочной.
Квадратная матрица называется симметричной, если равны её элементы симметричные относительно главной диагонали, т.е. 
.
Например: 
.
Диагональной называется квадратная матрица, у которой все элементы, не принадлежащие главной диагонали, равны нулю.
Например: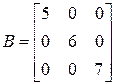 
.
----------------------------------------------------------------------------------------------------------------
Матрицы и действия над ними. Стр.1
Если у диагональной матрицы все числа главной диагонали равны между собой, то матрица называется скалярной. Например: 
.
Единичной называется диагональная матрица, у которой все элементы главной диагонали равны единице и обозначается E.
Например: 
.
Треугольной называется квадратная матрица, все элементы которой, расположенные по одну сторону от главной диагонали, равны нулю. Различают верхнюю и нижнюю треугольные матрицы.
Например: 
- верхняя треугольная матрица, 
- нижняя треугольная матрица.
Матрица, состоящая из одной строки, называется матрицей – строкой, а из одного столбца – матрицей-столбцом.
Например: 
, 
.
Две матрицы называются равными (A=B), если они имеют одинаковые размеры и их соответствующие элементы равны: 
Матрица 
, полученная из данной матрицы A заменой каждой её строки столбцом с тем же номером, называется транспонированной относительно А. Если матрица А имеет размеры 
, то 
Например: 
, 
.
Суммой матриц А и В называется матрица, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковые размеры.
Пример 1. Найти сумму матриц 
и 
.
Решение. 
Произведением матрицы А на число k называется матрица kA, каждый элемент которой равняется 
.
----------------------------------------------------------------------------------------------------------------
Матрицы и действия над ними. Стр.2
Пример 2. Найти 5А, если 
.
Решение. 5А= 
= 
.
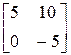Произведение матриц определяется для квадратных матриц одного и того же порядка, а также для прямоугольных матриц, у которых число столбцов первого множителя равно числу строк второго множителя.
Произведением матриц 
и 
называется матрица 
, каждый элемент которой 
равен сумме произведений элементов i-ой строки матрицы А на элементы j-го столбца матрицы В.
Произведение матрицы А на матрицу В обозначается АВ, при этом АВ≠ВА.
Пример 3. Найти произведение матриц 
и 
.
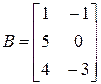Решение..
Целой положительной степенью 
(k>1) квадратной матрицы А называется произведение k матриц, каждая из которых равна А.
Нулевой степенью матрицы А называется единичная матрица того же порядка, что и А, т.е. 
.
Первой степенью матрицы А называется сама матрица А, т.е. 
.
Многочленом Р(А) от матрицы А называется выражение вида:
.
Многочлен от матрицы можно получить, если в обычный многочлен 
вместо х подставить квадратную матрицу А и учесть, что .
Определитель матрицы.
Каждой квадратной матрице A порядка n можно поставить в соответствие единственное число, которое вычисляется по определенному правилу. Это число называется определителем(детерминантом) матрицы A и обозначается | A | или det A, или Δ(A), Δ А. Порядок матрицы A является и порядком ее определителя. Определители порядка 1 и 2 вводятся соответственно равенствами:
Минором 
элемента aij, где 
называется определитель (n– 1)-го порядка, который состоит из элементов матрицы, полученной из данной путем «вычеркивания» i -й строки и j -го столбца.
Алгебраическим дополнением этого же элемента называетсячисло Аij =(–1) i+j M ij.
----------------------------------------------------------------------------------------------------------------
Матрицы и действия над ними. Стр.3
Теорема о разложении определителя по элементам строки или столбца: сумма произведений элементов любой строки (или столбца) данного определителя на их алгебраические дополнения равна этому определителю.
Свойства определителей.
1) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
2) перестановка двух строк (столбцов) меняет знак определителя на противоположный;
3) | A | = 0, если выполняется одно из следующих условий:
- в определителе есть нулевая строка (нулевой столбец);
- в определителе есть пропорциональные строки (столбцы);
- в определителе есть строки (столбцы), являющиеся линейной комбинацией соответствующих элементов других строк (столбцов);
4) если к элементам одной строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то значение определителя не изменится.
