МАТРИЦЫ
Определение. Матрица А размера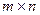 
(m строк, n столбцов) – это таблица чисел вида
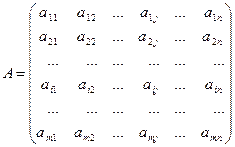
(1)
Сокращённые обозначения: 
,
- ая строка А, i = 1, 2, …, m,
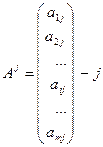-ый столбец матрицы А, j = 1, 2, … n,
- элемент матрицы А, находящийся на пересечении i – ой строки и j – го столбца.
При m ≠ n A называется прямоугольной матрицей, при m = n A называется квадратной матрицей порядка n.
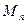- множество квадратных матриц порядка n.
Определение равенства матриц. Пусть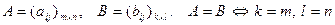 
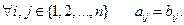
Операции над матрицами
Определение. Пусть . Транспонирование матрицы А – это переход от матрицы А к матрице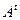 
размер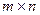а вида
,
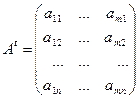строки которой – это столбцы матрицы А (см.(1)).
Очевидно, что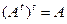 
.
Пример
Определение суммы матриц.
Пусть 
Тогда 
, то есть сумма матриц А и В одного размера 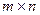- это матрица размера 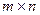, каждый элемент которой равен сумме элементов матриц А и В, расположенных на одинаковых местах (в i – ой строке и j – ом столбце) в этих матрицах.
Пример
Определение умножения матрицы на число. Пусть 
и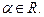 
Тогда 
, то есть для умножения матрицы на число нужно умножить на это число каждый элемент матрицы.
Определение умножения матриц. Пусть 
Только для матриц таких размеров (при которых длина l строки матрицы А равна высоте l столбца В) определено их произведение
,
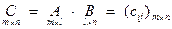где для 
(2)
В (2) использовано стандартное сокращенное обозначение суммы нескольких величин:
Формулу (2) легко запомнить так:
элемент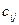 
матрицы 
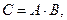расположенный в i – ой строке и j – ом столбце матрицы С, равен «скалярному» произведению i – ой строки 
матрицы А на j – ый столбец 
матрицы В.
. (3)
Пример
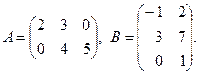Их произведение определено:
По формуле (2) или (3)
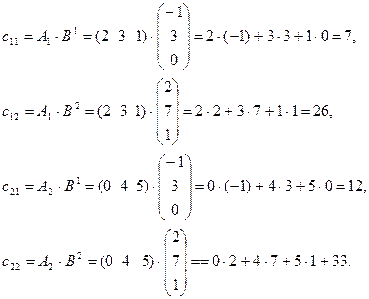
Следовательно, 
Свойства сложения матриц, умножения матрицы на число и умножения матриц аналогичны свойствам сложения и умножения действительных чисел, но умножение матриц не коммутативно: в общем случае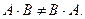 
В рассмотренном примере умножения матриц 
- матрица 
, но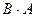 
будет матрицей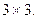 
Определение. Единичная матрица Е порядка n - это квадратная матрица порядка n вида
Е имеет свойства, аналогичные свойствам 1 при умножении действительных чисел: можно проверить, что для любой матрицы А размером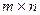 
и 
.
Матричный вид системы линейных уравнений
Рассмотрим СЛУ из n уравнений с n неизвестными 
:
(4)
Определим для этой СЛУ следующие матрицы:
- квадратная матрица порядка n, называемая матрицей СЛУ,
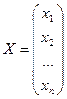- столбец неизвестных СЛУ, который является матрицей размера 
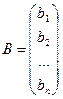- столбец свободных членов СЛУ, матрица размера 
Теперь СЛУ (4) можно записать в матричном виде
, (5) так как
. 
= 
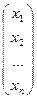Полученный матричный вид (5) СЛУ напоминает общий вид одного уравнения с одним неизвестным х:
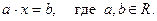При 
оно имеет единственное решение: так как существует обратное к а число 
и
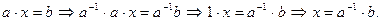
Возникает вопрос: можно ли аналогично решить СЛУ (5) – найти обратную к А матрицу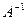 
и записать решение СЛУ (5) в виде
Но мы пока не знаем, что такое матрица 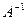, обратная к матрице А, и для каких матриц А существует .
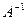