Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 
или 
.
Таким образом, 
.
30) Точка пересечения прямой и плоскости.
31) Квадратичные формы. Запись, обозначения. Матрица квадратичной формы.
Определение квадратичной формы
Квадратичная форма переменных 
- функция
- коэффициенты квадратичной формы. Без ограничения общности считают 
тогда
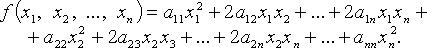
Если переменные принимают действительные значения и 
квадратичная форма называется действительной.
Матричная запись квадратичной формы
Матрица
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если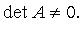 
33) Приведение квадратичной формы к диагональному виду методом ортогональных преобразований.
Ортогональное преобразование пространства 
:
где 
- собственные значения матрицы A.
34) Знакоопределенность матрицы. Критерий Сильвестра.
Классификация действительных квадратичных форм
Положительно-определенные
Квадратичные формы, для которых 
таких, что 
Нормальный вид 
Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны 
(критерий Сильвестра).
Отрицательно-определенные
Квадратичные формы, для которых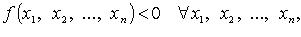 
таких, что Нормальный вид 
Квадратичная форма является отрицательно-определенной тогда и только тогда, когда 
Положительно-полуопределенные
Квадратичные формы, для которых 
таких, что Нормальный вид 
r < n, r = rank A.
Отрицательно-полуопределенные
Квадратичные формы, для которых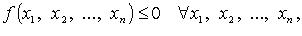 
таких, что Нормальный вид 
r < n, r = rank A.
Неопределенные
Квадратичные формы, которые принимают как положительные, так и отрицательные значения. Нормальный вид: 
r = rank A.
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Пусть квадратичная форма имеет в каком-то базисе матрицу
Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры Δ i положительны. Форма отрицательно определена, если и только если знаки Δ i чередуются, причём Δ1 < 0. Здесь главными минорами матрицы A называются определители вида
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица
не является неотрицательно определённой — так как, например, (Mv, v) = − 2 для v = (0,1, − 1). В то же время все её главные миноры равны 0, то есть неотрицательны.
35) Канонические уравнения линий 2-го порядка. Эллипс, гипербола, парабола.
Эллипс (рис. 4.14)
Каноническое уравнение: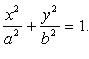 
Эксцентриситет: 
Уравнения директрис: 
Гипербола (рис. 4.15) нанизывается на ту ось, которая стоит со знаком плюс.
Каноническое уравнение: 
Эксцентриситет: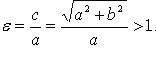 
Уравнения директрис:
Парабола (рис. 4.16) нанизывается на ту ось, которая стоит без квадрата. Если р>0 то ветви смотрят в сторону возрастания числовой оси.
Каноническое уравнение: 
Эксцентриситет: 
Уравнение директрисы: 
36) Поверхности 2-го порядка: цилиндры.
Цилиндр – одна переменная отсутствует. Идет вдоль той оси, переменная которой отсутствует.
X2 + Y2 = 1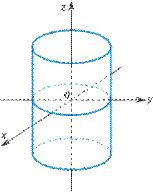 
37) Канонические уравнения поверхностей 2-го порядка: эллипсоид, конус и «седло».
Эллипсоид (рис. 4.18)
Каноническое уравнение:
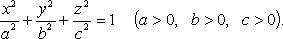
- трехосный эллипсоид;
- эллипсоид вращения вокруг оси Oz;
- эллипсоид вращения вокруг оси Oy;
- эллипсоид вращения вокруг оси Ox;
- сфера.
Конус второй степени (рис. 4.19)
Каноническое уравнение:
a = b - конус вращения (прямой круговой).
Гиперболический параболоид (седло).
Уравнение гиперболического параболоида:
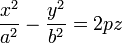
При сечении гиперболического параболоида плоскостью z = z0 поверхность порождает гиперболу.
При сечении гиперболического параболоида плоскостью x = x0 или y = y0 поверхность порождает параболу.
38) Канонические уравнения поверхностей 2-го порядка: гиперболоиды (одно и двуполостные).
Два плюса, один минус – гиперболоид. Там где минус – нанизывается поверхность.
Однополостный гиперболоид (рис. 4.20)
Каноническое уравнение:
a = b - однополостный гиперболоид вращения вокруг оси Oz.
Двуполостный гиперболоид (рис. 4.21)
Каноническое уравнение:
a = b - двуполостный гиперболоид вращения вокруг оси Oz.
Эллиптический параболоид (рис. 4.22)
Каноническое уравнение:
p = q - параболоид вращения вокруг оси Oz.
