МАТРИЦЫ
3.1. Предварительные сведения. Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:
.
Для обозначения матрицы используют прописные латинские буквы, для обозначения элементов матрицы – строчные латинские буквы с указанием номера строки и столбца, на пересечении которых стоит данный элемент. Запись «матрица B имеет размер m x n» означает, что речь идет о матрице, состоящей из m строк и n столбцов. Например, матрица 
имеет размер 2 x 3. Далее, bij - обозначение элемента, стоящего на пересечении i -й строки и j- го столбца данной матрицы (в примере b23=5).
При ссылке на i-ю строку матрицы A используют обозначение Ai, при ссылке на j-й столбец – обозначение Aj.
Матрица, у которой число строк совпадает с числом столбцов, называется квадратной. Элементы a11, a22 ,…, ann квадратной матрицы A (размера n x n) образуют главную диагональ. Квадратная матрица, у которой отличные от нуля элементы могут стоять только на главной диагонали, называется диагональной. Диагональная матрица, у которой все элементы (главной диагонали!) равны 1, называется единичной. Наконец, квадратная матрица, у которой ниже (выше) главной диагонали находятся только нули, называется верхней (нижней)треугольной матрицей. Например, среди квадратных матриц размера 3 x 3
, 
, 
, 
матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной.
Матрицы A, B называются равными (A=B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают.
Арифметические действия с матрицами.
Чтобы умножить матрицу A на отличное от нуля вещественное число k, необходимо каждый элемент матрицы умножить на это число:
.
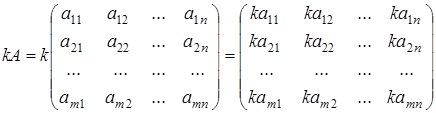Чтобы найти сумму матриц A, B одной размерности, необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах):
.
Пример 3.1. Найти 2A-B, если 
, 
.
Решение. Сначала умножаем матрицу A на число "2", затем матрицу B на число "-1", и, наконец, находим сумму полученных матриц:
Произведение AB можно определить только для матриц A размера m x n и B размера n x p, при этом AB=C, матрица C имеет размер m x p, и ее элемент cij находится как скалярное произведение i-й строки матрицы A на j-й столбец матрицы B: 
(i=1,2,...,m; j=1,2,...,p). Фактически необходимо каждую строку матрицы A (стоящей слева)умножить скалярно на каждый столбец матрицы B (стоящей справа)
Пример 3.2. Найти произведение матриц 
и 
.
Решение. Размер матрицы A 3 x 2, матрицы В 2 х 2. Поэтому произведение АВ найти можно, произведение ВА – нет. Действуя по сформулированному выше правилу, получаем:
Матрицей, транспонированной к матрице A размера m x n, называется матрица AT размера n x m, строки которой являются столбцами исходной матрицы.
Например, если 
, то 
.
Пример 3.3. Найти 
.
Решение. Воспользовавшись вычислениями, проведенными при решении примера 3.2, а также правилами умножения матрицы а число и сложения матриц, получим:
.
3.3. Элементарные преобразования матриц. К таким преобразованиям матриц относятся следующие действия:
1) перемена местами двух строк матрицы (краткая запись: 
);
2) вычеркивание нулевой строки (в которой все элементы равны нулю);
3) умножение всех элементов одной строки матрицы на одно и то же число, отличное от нуля (коротко: 
);
4) прибавление к элементам одной строки матрицы соответствующих элементов другой ее строки, умноженных на одно и то же отличное от нуля число (коротко: 
).
Вычеркивание нулевой строки приводит к изменению размера матрицы, поэтому говорить о равенстве матриц при подобных преобразованиях нельзя.
Матрицы A, B называются эквивалентными, если одна получена из другой путем элементарных преобразований.
Матрица A размера m x n называется ступенчатой, если в каждой ее строке есть элемент, в столбце которого все элементы ниже являются нулями, а в последней строке есть хотя бы один ненулевой элемент. Упомянутые в определении ненулевые элементы называют ведущими.
Примеры ступенчатых матриц: 
, 
. Любая верхняя (нижняя) треугольная матрица или диагональная матрица также является ступенчатой.
Теорема 3.1. Любую ненулевую матрицу можно путем элементарных преобразований свести к эквивалентной ей ступенчатой матрице.
Пример 3.4. Привести к ступенчатому виду матрицы 
, 
.
Решение. При преобразованиях матрицы A в качестве ведущего элемента в первой строке рассматриваем a13, во второй – a21. Имеем:
.
Последняя матрица является ступенчатой, причем ведущим элементом в третьей строке является a32. Итак, 
.
Проведем преобразования для матрицы B.
.
Итак, 
. В данном случае в первой строке ведущим является элемент b11, во второй в качестве ведущего может выступить либо b22, либо b24.
Замечание 1. Обобщением элементарных преобразований 2)-4) является возможность вычеркивания равных или пропорциональных строк матрицы (при этом одна из таких строк обязательно должна остаться!).
Замечание 2. Аналогичные элементарные преобразования можно проводить со столбцами матриц.
Рангом матрицы A в дальнейшем будем считать число строк эквивалентной ей ступенчатой матрицы, используя обозначение r(A). Так, в рассмотренном выше примере 3.4 r(A)=3, r(B)=2. Можно доказать, что ранг матрицы A (размера m x n) не может быть больше 
(например, для матрицы А размера 2 x 3 
). Кроме того, ранг матрицы не зависит ни от выбора ведущих элементов, ни от проводимых преобразований. Это свойство можно использовать при проверке. Так, в примере 3.4 после перестановки первой и второй строки в матрице B можно в качестве ведущего сначала рассмотреть элемент b12, а затем вычеркнуть третью строку, пропорциональную второй (
):
Мы получили другую матрицу, эквивалентную B. Но она тоже является ступенчатой, причем состоит из двух строк, r(B)=2, как и было показано ранее.
