Решения задач I-го тура студенческой олимпиады по математике 2011 года
I Элементарная математика
Тема 1.
Геометрия – площади и периметры
Задача 1 Доказать, что квадрат нельзя разделить на три треугольника одинаковой площади
Доказательство
Предположим противное, то есть что квадрат можно разделить на
три треугольника равной площади.
Так как треугольника – три, а сторон квадрата – четыре, то у какого-то треугольника две стороны будут принадлежать двум сторонам квадрата, и ясно, что соседним, а не противоположным,
так как стороны треугольника – не параллельны. Пусть эти две
стороны находятся на 
и 
. Тогда 
- их общая вершина, так как стороны треугольника должны пересекаться в его вершине.
Логические варианты расположения этого треугольника
представлены на рисунках 2-4.
Рисунок 2 отпадает, так как остается пятиугольник, который не разделяется на два треугольника, а только на три и более.
Рисунок 4 отпадает, так как площадь треугольника становится раной половине площади квадрата, что больше, чем одна треть
его площади. Рассмотрим рис 3. Оставшийся четырехугольник
можно разделить на два треугольника только диагональю.
Если делим четырехугольник диагональю 
, то площадь треугольника 
равна 
.Если делим четырехугольник диагональю 
, то площадь треугольника 
равна .
Что и требовалось доказать (Ч.Т.Д.)
Замечание. Эта задача родилась, как частный случай одной
теоремы, доказанной в 70-е годы 20-го века. Заметим, что квадрат
легко разрезать на любое четное число равных, а поэтому равных и по площади треугольников.
Вот эта теорема: квадрат нельзя разрезать на нечетное (3,5,7,…) число треугольников одинаковой площади.
Задача 2 Доказать, что параллелограмм нельзя разделить на три треугольника одинакового периметра
Доказательство
Предположим противное, то есть, что параллелограмм можно разделить на три треугольника равного периметра.
Так как треугольника – три, а сторон параллелограмма – четыре, то у какого-то треугольника две стороны будут принадлежать двум сторонам параллелограмма, и ясно, что соседним, а не противоположным, так как стороны треугольника – не параллельны. Пусть эти две стороны находятся на и . Тогда - их общая вершина, так как стороны треугольника пересекаются в его вершине. Рисунок 5 отпадает, так как остается пятиугольник, который не разделяется на два треугольника, а только на три и более. Рисунок 7 отпадает, так как один из треугольников 
останется целым, а другой придется разделить на два, периметры
которых станут меньше, чем периметры треугольников .
Рассмотрим рис 6. Четырехугольник 
делится на два треугольника только диагональю или .
Рассмотрим оба случая:
Рисунок 6.1
Проведем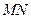 
. Тогда 
; 
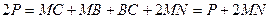. Отсюда 
,
, 
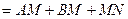. Но тогда точка 
совпадает с точкой 
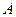и вместо трех, мы получаем два треугольника. Противоречие.
Рисунок 6.2
. 
.
. 
. Нарушается неравенство треугольника 
о том, что сумма двух сторон треугольника больше третьей. Мы пришли к противоречию c предположением, что параллелограмм можно разделить на три треугольника одинакового периметра. Значит доказано, что параллелограмм нельзя разделить на три треугольника одинакового периметра.
Замечание. Параллелограмм легко разрезать на четное число
равных, а потому равных и по периметру треугольников.
Возникает и общая проблема: можно ли разрезать квадрат на
нечетное число треугольников с одинаковым периметром?
Задача 3 Доказать, что в любую выпуклую плоскую фигуру площади 
можно вписать выпуклый четырехугольник площади 
.
Доказательство
Пусть задана на плоскости плоская выпуклая фигура 
.
Пусть точки 
- самые удаленные друг от друга точки фигуры.
Развернем фигуру так, чтобы отрезок 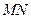стал горизонтальным.
Вся фигура окажется внутри вертикальной полосы между прямыми 
и 
, иначе точки и 
- не самые удаленные друг от друга.
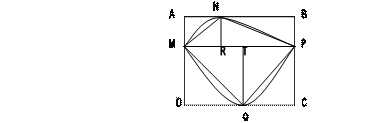
Проведем теперь сверху и снизу фигуры две горизонтальные прямые, которые касаются ее в точках 
- соответственно.
Фигуру поместили в прямоугольник 
. Тогда 
. Поэтому 
. Ч.Т.Д.
Замечание Интересно было бы найти аналогичное свойство для объемов выпуклых тел в пространстве.
Тема 2
