Это распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия. Распределение Больцмана было открыто в 1868 - 1871 гг. австралийским физиком Л. Больцманом. Согласно распределению, число частиц ni с полной энергией Ei равно: 
где ωi - статистический вес (число возможных состояний частицы с энергией ei). Постоянная А находится из условия, что сумма ni по всем возможным значениям i равна зад
32. Скорость движения шара вниз по наклонной плоскости. Определим ускорение шара из известной формулы:
Fg•sinα = m•a
a = Fg•sinα/m
Fg = m•g
a = m•g•sinα/m = g•sinα
Ускорение шара вдоль наклонной плоскости не зависит от массы шара, а только от угла наклона плоскости.
47.Вычисление средних значений. Плотность вероятности. величина x может принимать ряд дискретных значений x1+x2+…+xn. Поскольку количество молекул, у которых x=xi, равно NP(xi), сумма
значений величины x у всех этих молекул выражается произведением xiNP(xi). Для того, чтобы получить сумму значений x у всех молекул газа, необходимо найти сумму всех
произведений: x1NP(x1)+x2NP(x2)+…+xnNP(xn)=
Разделив эту сумму на N, получим среднее значение x:
<X>=сумма xiP(xi)
Предположим теперь, что величина x изменяется непрерывно в промежутке a<=x<=b.
В такой ситуации число возможных значений x бесконечно велико, а количество молекул газа очень велико, но все же конечно. Поэтому вопрос о том, какое количество молекул обладает точно заданным значением x, не имеет смысла – это количество равно нулю. В
этом случае правомерен следующий вопрос: какова вероятность dP того, что молекулы газа имеют значения x, заключенные в элементарном промежутке от x до x+dx? Понятно, что эта вероятность пропорциональна протяженности этого промежутка (dx); кроме того,
она зависит от численного значения величины, т.е. пропорциональна некоторой функции x:
dP=f(x)dx
Отсюда находим, что f(x)=dP/dx
Функция, определяемая равенством, называется функцией распределения вероятностей (плотностью вероятности). Из определения следует, что эта функция, найденная для конкретного значения x, численно равна вероятности того, что величина
x находится на промежутке единичной протяженности. Именно поэтому функция называется также плотностью вероятности.
36.Периоды колебаний физического и математического маятников. Математический маятник представляет собой частицу массой m, подвешенную на невесомой нерастяжимой нити. 
Учтем, наконец, что для математического маятника 
Физический маятник представляет собой протяженное тело, имеющее ось вращения, проходящую через любую точку тела, за исключением центра масс. 
53. Распределение Больцмана. Заменив в барометрической формуле давление через nkT, 
получим закон изменения с высотой числа молекул в единице объёма: 
, где 
- масса 1-ой молекулы, k – постоянная Больцмана, 
- число молекул в единице объёма на высоте, равной 0, n – то же число на высоте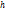 
. Из формулы: с понижением температуры число частиц на высотах, отличных от нуля, убывает, обращаясь в 0 при Т=0. При высоких температурах, напротив, n слабо убывает: все молекулы оказываются распределёнными по высоте почти равномерно, т.к. каждое распределение молекул по высоте устанавливается в по принципу:1) притяжение молекул к земле mg стремиться расположить их на поверхности земли; 2) тепловое движение kT стремиться разбросать молекулы равномерно по высотам. На разной высоте молекула обладает различным запасом потенциальной энергии: 
. Следовательно, распределение молекул по высоте является и распределением их по значениям потенциальной энергии. Объединив закон изменения с высотой числа молекул в единице объёма формулу запаса потенциальной получим распределение Больцмана: 
где 
и 
– число молекул в точках, где потенциальная энергия имеет значения 
и 
. Распределение справедливо в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. закон Максвелла даёт распределение частиц по значениям кинетической энергии, закон Больцмана даёт распределения частиц по значениям потенциальной энергии. Распределения Максвелла и Больцмана можно объединить в один закон Максвелла-Больцмана, согласно которому содержащееся в единице объёма количество молекул, скорость которых лежит между 
, равно: 
.
