Закон сохранения энергии. Внутренняя энергия

полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной. Если в замкнутой системе действуют также неконсервативные силы, то полная механическая энергия системы не сохраняется 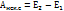. Вну́трення эне́ргия тела — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы.

 

21/Момент импульса. /Его сохранение

Моментом импульса частицы относительно некоторой точки О называется векторная (псевдовекторная) величина . Свойства: 1) Зависит от выбора точки О; 2) Модуль L=rpsin = ; 3) L – плечо, . Моментом импульса относительно некоторой оси называют проекцию момента импульса на эту ось. При движении частицы с постоянной скоростью момент импульса сохраняется. Закон сохранения момента импульса.

Скорость изменения момента импульса механической системы = сумме моментов внешних сил, действующих на систему . Если система замкнута (), то выполняется закон сохранения момента импульса: момент импульса замкнутой системы материальных точек остаётся постоянным. Закон сохранения момента импульса выполняется также для незамкнутых систем, если суммарный момент внешних сил = 0.

 

Движение в центральном поле сил.

Пусть частица массы m движется в центральном силовом поле. Момент сил, действующих на частицу момент импульса частицы . В силу сохранения , направление движения частицы должно происходить перпендикулярно направлению . Частица совершает плоское движение. Для описания движения воспользуемся полярной системой координат: , – проекция моментов на ось Z сохраняется. Т.к. силовое поле является центральным, то оно консервативное, значит, для него можно найти выражение для потенциальной энергии U. При движении в консервативном силовом поле сохраняется полная механическая энергия. , таким образом, задача по движению частицы в центральном силовом поле свелась к решению системы 2-ух дифференциальных уравнений 1-ого порядка. При этом мы используем момент энергии и момент сил.

 

 

Момент инерции.

Момент инерции определяется как , если распределение массы равномерно, то заменяется на – элементарный объём, – плотность вещества. .

Момент инерции:

1) однородного тонкого стержня массы , длины относительно оси, проходящей через центр масс и перпендикулярной стержню:

2) однородного тонкого стержня массы , длины относительно оси, проходящей через один из концов стержня: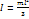

3) тонкого кольца массы , радиуса R относительно оси симметрии, перпендикулярной плоскости кольца:

4) однородного диска (цилиндра) массы , радиуса R, высоты h относительно оси симметрии, перпендикулярной основанию: .

Затухающие колебания.

В реальных физических системах всегда действуют силы сопротивления, в результате действия которых амплитуда колебаний с течением времени убывает. рассмотрим движение тела в вязкой среде, когда силы сопротивления противоположны скорости движения тела: , 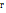– коэффициент сопротивления. . Подставим вместо – дифференциальное уравнение 2-ого порядка сводится к квадратному алгебраическому уравнению . Колебательный процесс возможен, если силы сопротивления достаточно малы. Это означает, что должно выполняться условие . В этом случае . Следовательно, общим решением нашего уравнения будет функция – кинематический закон затухающих колебаний. Можно сказать, что наблюдаются гармонические колебания с частотой , амплитуда же колебаний убывает по экспоненциальному закону . Скорость затухания определяется величиной коэффициента затухания . Затухание характеризуется также декрементом затухания, который показывает во сколько раз уменьшилась амплитуда колебаний за время, равное периоду : . Логарифм этого выражения называют логарифмическим декрементом затухания: 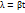. В затухающих системах используется также такая величина как добротность: .

 

40/Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (вынуждающая сила). Пусть вынуждающая сила меняется по гармоническому закону . С учётом сил сопротивления и упругости получим динамическое уравнение движения системы: Предположим, что система совершает гармонические колебания с частотой , отставая по фазе от вынуждающей силы на . Находим 1-ую и 2-ую производные и подставляем в динамическое уравнение движения системы: . В левой части стоит сумма 3-х колебаний одинаковой частоты, сдвинутой по фазе и с различными амплитудами. При фаза результирующих колебаний должна равняться 0. С помощью векторной диаграммы определили амплитуду результирующих колебаний .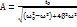

Начальная фаза определена условием: .

При некоторой определённой для данной системы частоте , амплитуда достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а частота – резонансной частотой. , .

 

10.РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. F=-gradU.

Рассмотрим движение материальной точки в некотором силовом поле F. Если под действием силы F материальная точка прошла dS. 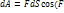,dS) - работа силы F на пути dS. Для того, чтобы определить А сил поля, не на бесконечно-малом, а на конечном пути, нужно разбить этот путь на бесконечно-малые участки dS.Работа сил поля при переносе частиц из одной точки в другую не зависит от траектории, а определяется лишь положением начальной и конечной точек. Величина U, т.е. взятая с обратным знаком A при переходе частицы из точки О в точку Р называют потенциальной энергией частицы в точке Р. Работа силового поля А12 при переходе тела из точки А12=U1-U2, где U1 и U2 значения потенциальной энергии в этих точках.dA=-dU; dA=FdS; F=-dU/dS;В общем случае:F=-gradU

30/Движение твёрдого тела.

Движение твёрдого тела можно представить как результат суммы поступательного (любая связанная с телом прямая перемещается параллельно самой себе, т.е. все точки тела движутся по одинаковым траекториям) и вращательного (все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемою осью вращения; все окружности лежат в параллельных плоскостях и перпендикулярно оси вращения) движений (неоднозначно). Произвольная точка твёрдого тела испытывает перемещение 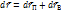, причём для всех точек тела одно и то же. Разделив на соответствующий промежуток времени , получим скорость точки: . – одинаковая для всех точек скорость поступательного движения, – скорость, обуславливаемая вращением (различная в разных точках). – радиус-вектор данной точки, – угловая, независящая от выбора точки О скорость. Следовательно, . Любое твёрдое тело можно представить как совокупность материальных точек массы , расстояние между которыми неизменно. Каждая материальна точка движется под действием, как внутренних сил, так и внешних. Движение определяется 2-ым законом Ньютона. . .Центр масс твёрдого тела движется таким же образом, как двигалась бы материальная точка массы под действием всех внешних сил. Движение твёрдого тела определяется 2-мя (3-мя) уравнениями:

1)

2) ;

3) – при плоском движении