Опред. Обыкновенным дифф. уравнением называют уравнение, связывающее независимую переменную х, искомую функцию у=у(х) и ее производные у′, у′′,…, уⁿ, т.е. уравнение вида
F(х, у, у′, у′′,…, уⁿ) = 0.
Опред. Порядком дифф. уравнения называется порядок наивысшей производной, входящей в уравнение.
Задача.
Найти решение дифф. уравнения (т.е. функцию у), которая удовлетворяет уравнению у′ = f(х).
Данное уравнение решается в теории неопределенных интегралов:
у = ∫f(х)dх
у = F(х) + С.
В общем случае дифф. ур. второго порядка можно записать в виде F(х; у; у′, у′′) = 0, где у = у(х) – искомая функция, у′ = у′(х) и
у′′ = у′′(х) – ее производные по х первого и второго порядков, а F – заданная функция переменных х; у; у′, у′′.
Дифф. ур. вида у′′ + ру′ + qу = f(х) (1), где р и q – некоторые числа, называют дифф. ур. второго порядка.
Если f(х)≡0, то уравнение (1) называется однородным.
Для решения однородного дифф. ур. второго порядка составляется характеристическое уравнение, которое имеет вид λ² + pλ + q = 0.
Характеристическое уравнение получается заменой у′′ на λ², у′ на
λ, q на 1.
Решая данное квадратное уравнение, находим λ1 и λ2.
Возможны три случая:
| λ1 ≠ λ2 действ., разл. корни | λ1 = λ2 = λ | λ1,2 = α ± βi компл., разл. корни |
| у0 = С1е λ1х + С2 е λ2х | у0 = (С1 + С2х) е λх | у0 = еαx(С1cosβx + С2sinβx) |
Теория вероятностей.
Статистика.
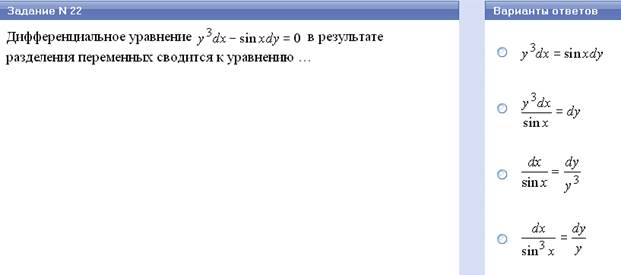
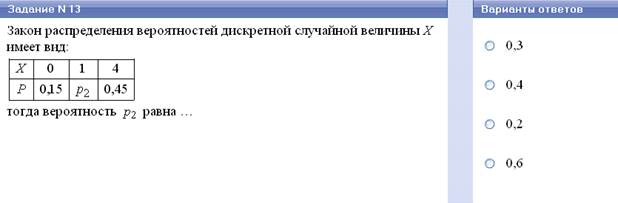
Закон распределения случайной величины удобно записывать в виде таблицы.
На первой строчке записывается значение случайной величины, а на второй – вероятность наступления события.
n
∑ pi = 1.
I=1
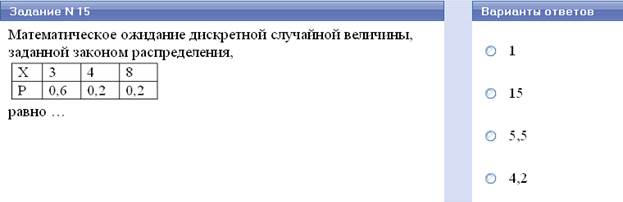
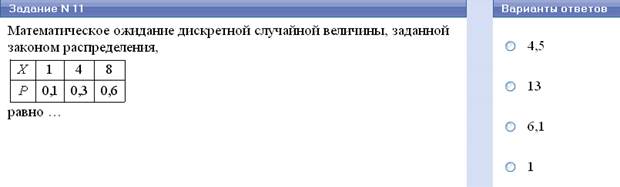
Математическим ожиданием случайной величины называется число, равное сумме произведений всех значений случайной величины на вероятности этих значений, т.е.
n
МХ = ∑ xipi
i=1
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Дисперсию находят по формуле:
ДХ = М(Х2) – (МХ)2
Ряды.
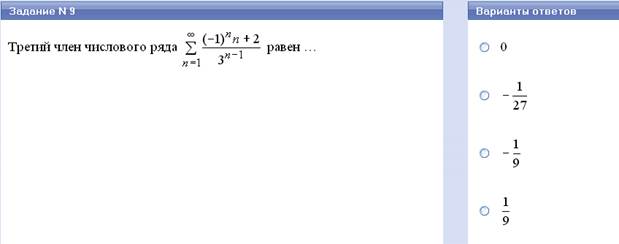
Пусть задана числовая последовательность аn, nЄN, тогда выражение а1+а2+ …+аn +… называется числовым рядом и обозначается ∞
∑ аn
n = 1
Числа а1, а2, …аn называются членами ряда, соответственно
первым, вторым и т.д. аn называется п-м или общим членом ряда,
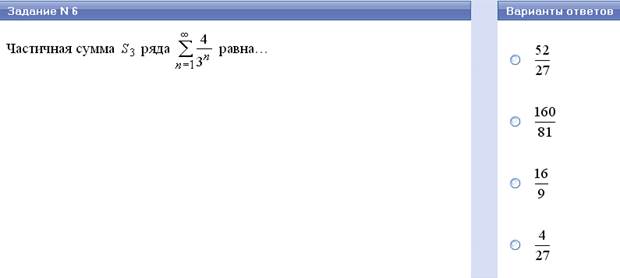
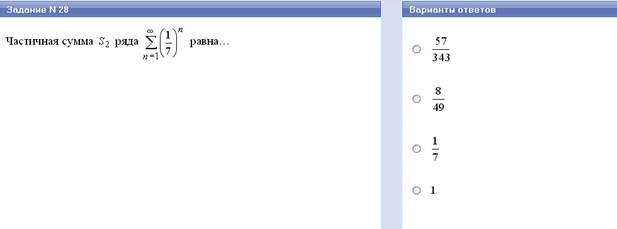
S1 = а1, S2 = а1+а2, …., Sn = а1+а2+ …+аn … называют частичными суммами ряда.
Необходимый признак сходимости, вообще говоря, не гарантирует сходимости ряда. Сходимость или расходимость ряда устанавливается с помощью достаточных признаков. Признаки сравнения, которые мы рассмотрим ниже, как раз и представляют собой достаточные признаки сходимости или расходимости рядов.
Если частичная сумма ряда 
при неограниченном возрастании n не имеет конечного предела (стремится 
к или 
), то такой ряд называется расходящимся.
Если ряд сходящийся, то значение при достаточно большом n является приближенным выражением суммы ряда S.
Так называемый обобщенный гармонический ряд 
сходится при p > 1 и расходится при 0 < p ≤ 1.
Признак Даламбера.
Если для ряда с положительными членами
выполняется условие 
, то ряд сходится при 
и расходится при 
.
Признак Даламбера не дает ответа, если 
.
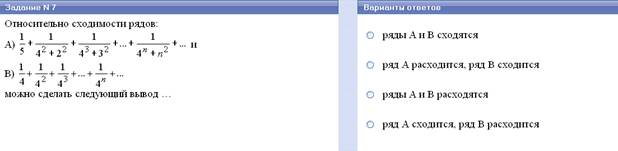
Признак сравнения.
∞ ∞
Пусть для рядов ∑ аn и ∑вn выполняется условие: существует N
n=1 n=1
такое что 0 ≤ аn ≤ вn для всех n ≥N.
Тогда, если ряд вn сходится, то и ряд аn сходится.
Если же ряд вn расходится, то и ряд аn расходится.
Если члены ряда:
числа, то ряд называется числовым;
числа одного знака, то ряд называется знакопостоянным;
числа разных знаков, то ряд называется знакопеременным;
положительные числа, то ряд называется знакоположительным;
числа, знаки которых строго чередуются, то ряд называется знакочередующимся;
функции, то ряд называется функциональным;
степени, то ряд называется степенным;
тригонометрические функции, то ряд называется тригонометрическим.
