Погрешности.
Округление чисел.
Способ (округление с наименьшей погрешностью).
А) единицы младших разрядов отбрасываются.
В) число единиц данного разряда не меняется, если первая отбрасываемая цифра меньше 5,
И увеличивается на 1, если первая отбрасываемая цифра больше или равна 5.
Пример: округлить число до целых, до десятых, до сотых, до наивысшнго разряда.
231,7298 ≈ 232 ≈231,7 ≈ 231,73 ≈ 200.
Способ (с недостатком).
Все цифры дроби до данного разряда включительно не меняются, а цифры младших разрядов заменяются 0.
231,7298 ≈ 231≈ 231,7 ≈231,72 ≈ 200.
Способ (с избытком)
Все цифры дроби до данного разряда не меняются, данный разряд увеличивается на 1, а цифры младших разрядов заменяются 0.
231,7298 ≈ 232 ≈ 231,8 ≈231,73 ≈ 300.
Приближенные значения и погрешности приближений.
Пусть х – результат измерения некоторой величины.
А - некоторая точность измерения.
Опред. Тогда а называется приближенным значением (приближением) величины х.
Если а ≤ х, то а – приближенное значение с недостатком (приближение снизу).
Если а ≥ х, то а - приближенное значение с избытком (приближение сверху).
Таким образом, если х – точное значение,
а – приближенное значение, то
х – а – погрешность приближения.
Обозначение: ∆х = х – а → х = ∆х + а.
Т.е. истинное значение равно приближенному значению плюс погрешность.
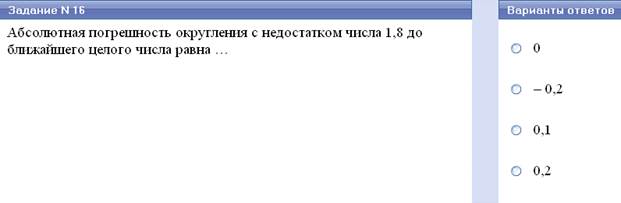
Опред. Модуль разности точного и приближенного значений называется абсолютной погрешностью приближения, т.е. l∆хl = lх – аl.


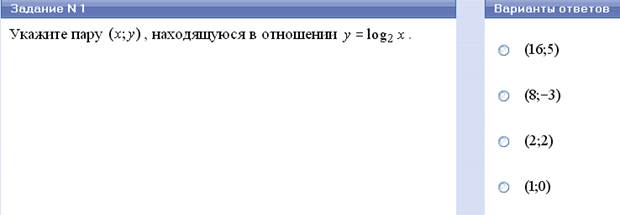
Соответствия между переменными х и у.


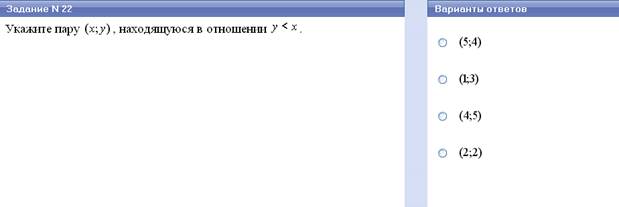

Соответствия между множествами.
Даны два множества А и В.
Опред. Множество, состоящее из всех элементов, принадлежащих и множеству А и множеству В, называется пересечением множеств А и В.
Опред. Множество, состоящее из всех элементов, принадлежащих или множеству А или множеству В, называется объединением множеств А и В.
Опред. Разностью множеств А и В называют множество, состоящее из всех элементов множества А не принадлежащих множеству В.

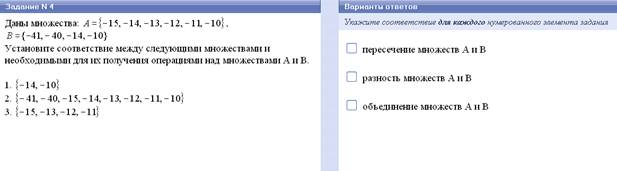

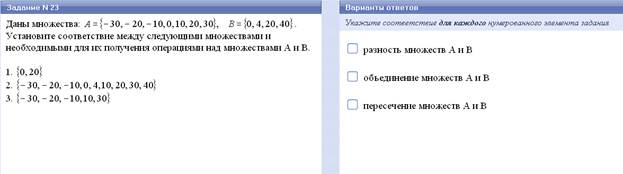

Утверждения о числовых множествах.





Дифференцирование.
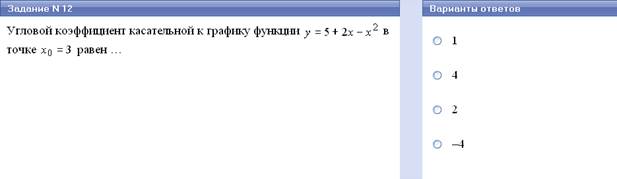
Число к = tg α называют угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох.
Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке. Т.о. f Ι(х) = tgα = к.
При вычислении производной используются следующие правила дифференцирования суммы, произведения и частного:
1. (c f(x))'=c f'(x); c=const
2. (f(x) ± g(x))'=f'(x) ± g'(x)
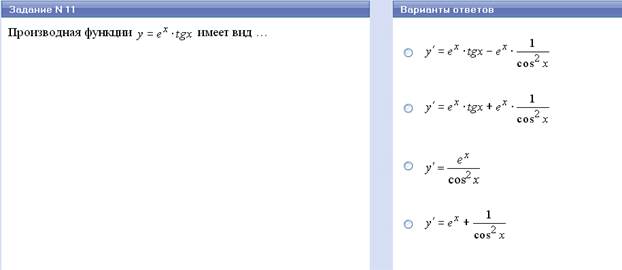
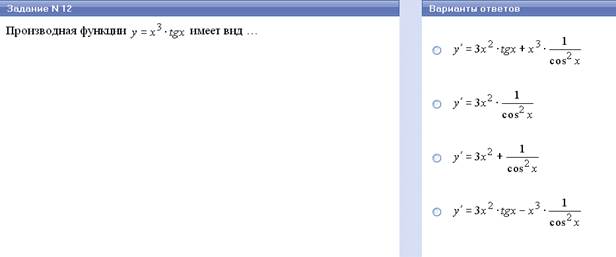
3. (f(x) • g(x))'= f '(x) • g(x)+ f(x) • g'(x)
4. (f(x)) l = f '(x) • g(x) - f(x) • g'(x)
g(x) g2(x)
5. f(g(x))'=f '(g(x))•g'(x)
Таблица производных.
| Функция | Производная |
| С=const | |
| x | |
| х p | pхp-1 |
| 1 x | -1 х2 |
| kx+b | k |
| (kx+b)p | kр(kx+b)рˉ¹ |
| √x | 1 (2√х) |
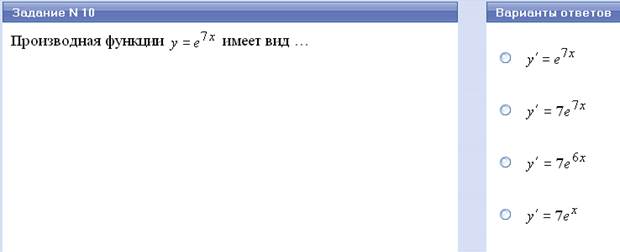
| ℮ˣ | ℮ˣ |
| lnx | 1 x |
| sin x | cos x |
| cos x | -sin x |
| tg x | 1 cos²x |
| ctg x | -1 sin²x |
| logаx | 1 x ln а |
| Arcsin x | 1 √1-x² |
| Arcos x | –1 √1-x² |
| ℮кх + в | к℮кх + в |
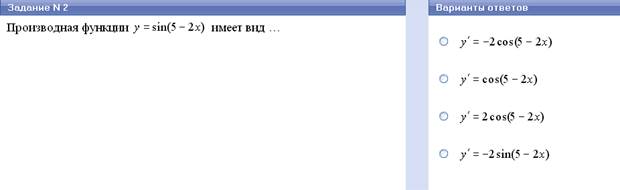
| sin (кx + в) | кcos (кx + в) |
| cos (кx + в) | - sin (кx + в) |
| ln (кx + в) | к кx + в |
| ах | ахlnа |
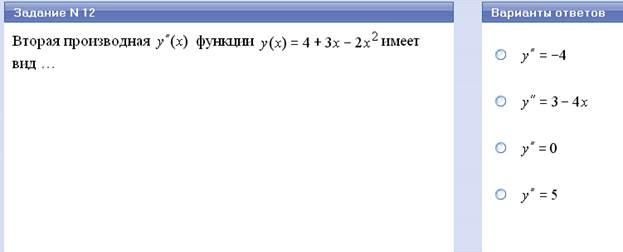
Вторая производная – производная от первой производной данной функции.













Интегрирование.
Определение. Функция F(х) называется первообразной функции f (х) на некотором промежутке, если для всех х из этого промежутка выполняется равенство
Fl(х) = f(х).
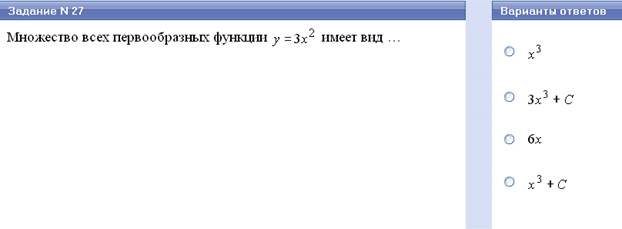

Таблица первообразных.
| функция | первообразная |
| х + С | |
| х р, р ≠ - 1 | х р+1 + С р+1 |
| 1 х, х > 0 | ℓn х + С |
| ех | ех + С |
| sin х | - cosх + С |
| cosх | sin х + С |
| (кх+в)р, р ≠ - 1, к ≠ 0 | (кх+в) р+1 + С к(р + 1) |
| 1 кх +в, к ≠ 0 | 1 · ℓn(кх + в) + С к |
| е кх + в, к ≠ 0 | 1 · е кх + в + С к |
| sin(кх+в), к ≠ 0 | - 1 · cos(кх+в) + С к |
| сos(кх+в), к ≠ 0 | 1 · sin(кх+в) +С к |
В в
∫ f(х) dх = F(х) = F(в) – F(а). о П а а


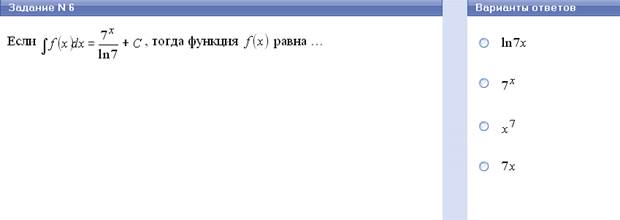
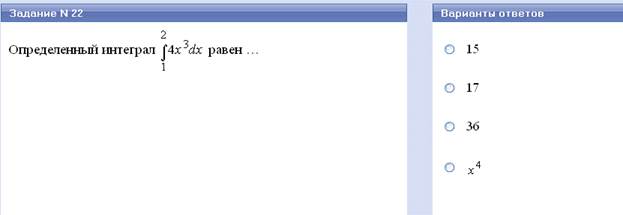



Метод замены переменной заключается в том, чтобы для подынтегрального выражения f(х)dx подбирают такую функцию у = φ(х), чтобы подынтегральное выражение могло быть записано в виде f(х)dx = g(φ(x) · φ′ (x)dx.
В данных примерах подстановка уже дана. Необходимо заменить dx на dt.
















