1. Активная длительность фронта экспоненциальной формы. Фронтовая часть импульса часто выражается аналитически экспоненциальной функцией времени (рис. 7)
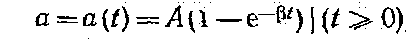, (2.10)
где 1/β =θ — постоянная времени экспоненты.
Согласно формуле (2.3), активная длительность фронта определяется моментами t’0,1 и t’0,9, в которые величина импульса равна соответственно 0,1А и 0,9A; эти моменты находятся из уравнений
Так как β t’0,1 < < 1, то уравнение (а) можно упростить, используя для этого первые два члена разложения в ряд функции
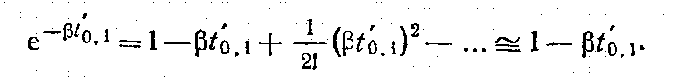
Подставив последний двучлен в уравнение (а), получим
(в)
Решая уравнение (б), найдем
(г)
Учитывая равенства (в) и (г), из формулы (3) получим
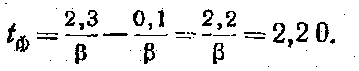(2.11)
Таким образом, активная длительность фронта экспоненциальной формы в 2,2 раза больше постоянной времени θ.
2. Экспоненциальный импульс. Определим активную длительность экспоненциального импульса (рис. 8), выражаемого функцией
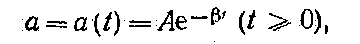(2.12)
где 1/β =θ — постоянная времени экспоненты.
| Рис. 7. Рис. 8. |
Согласно формуле (2.2) активная длительность импульса определяется моментами t’0.5 и t’’0.5, в которые величина импульса равна 0,5А. Так как в данном случае длительность фронта импульса равна нулю, то t’0.5 =0. Момент t’’0.5 — корень уравнения
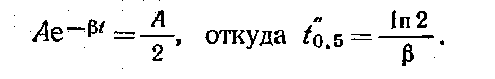
Подставляя найденные значения в формулу (2.2), получим
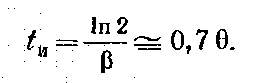(2.13)
Таким образом, активная длительность экспоненциального импульса доставляет примерно 70% от постоянной времени θ.
3. Экспоненциальный импульс лишен плоской вершины, После мгновенного достижения высоты А сразу же начинается срез импульса Найдем его длительность. Замечаем, что при t > 0 функция (2.12) может быть представлена в виде разности А—[А (1 — e—βt)], где выражение в квадратных скобках совпадает с функцией (2.10). Следовательно, как это вытекает из формул (2.3), определение длительности среза экспоненциального импульса не отличается от определения длительности фронта, изменяющегося по экспоненциально-му закону (см. п. 1), поэтому активная длительность среза экспоненциального импульса
tc = 2,2θ (2.14)
4. Двухэкспоненциальный импульс — импульс, выражаемый разностью двух экспоне-нциальных функций:
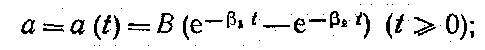(2.15)
он имеет вид, показанный на рис. 9. Здесь при положительной полярности импульса
β1< β2, и экспонента с постоянной времени θ2 = 1/ β2 определяет, в основном, восходящую часть импульса (фронт), а экспонента с постоянной времени θ1 = 1/ β1 определяет, в основном, падающую часть импульса (срез). В формуле (2.15) величина В не равна высоте А импульса, что ясно из приведенного на рис. 10 (в несколько уменьшенном масштабе) построения; здесь пунктирными линиями изображены графики двух составляющих
функции (2.15), разность которых представляет график рассматриваемого импульса. Как видно, В > А.
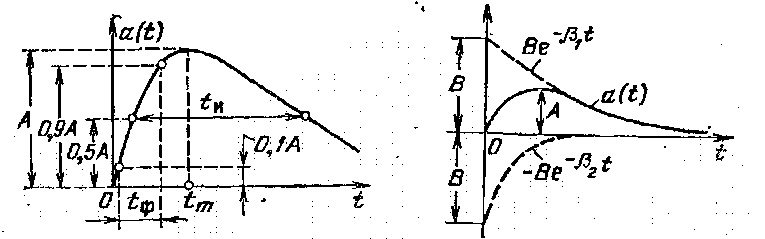
| Рис. 9. Рис. 10. |
Продифференцировав функцию (2.15) по времени, из условия da/dt=0 можно найти момент
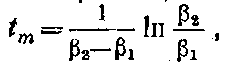в который функция a(t) достигает максимума amax = a(tm) =A. Отсюда можно найти высоту импульса
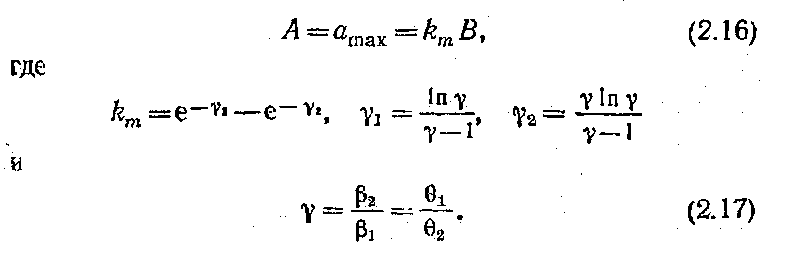
График зависимости km = km(γ) приводится на рис. 11. Он позволяет по заданию величины В найти высоту А из равенства (2.16). При малых значениях γ < 2 высота
А<< В; при γ > 10 высота А приближается к В.
5. Из численного решения трех трансцендентных уравнений
| Рис 11. |
находятся моменты времени t’0.5, t’’0.5, t’0.1, t’0.9, которые в соответствии с формулами (2.2) и (2.3) определяют активные длительности tи и tф. По данным таких вычислений постро-ены представленные на рис. II графики функций β1tи = Fи(γ) и β1tф = Fф(γ); они позволяют по заданным значениям β1 и β2 (или θ1 и θ2) найти активные длительности tи и tф. В практически наиболее важных случаях (γ > 1,5) можно (с погрешностью менее 10%) пользоваться приближенными формулами:
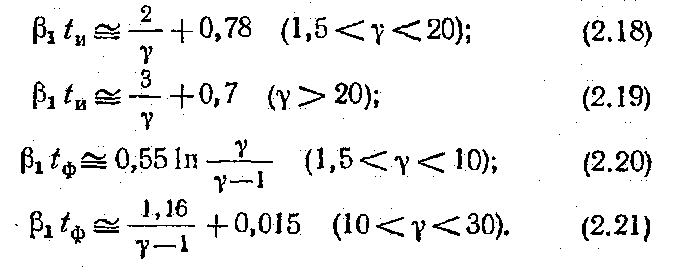
Из этих формул видно, что при γ → ∞ длительности tи → 0,7/β1 и t ф → 0. Такой результат согласуется с тем, что при γ → ∞ также и β2 → ∞, т. е. двухэкспоненциальный импульс вырождается в экспоненциальный импульс.
7. Колокольный импульс (рис. 12) выражается функцией
(2.22)
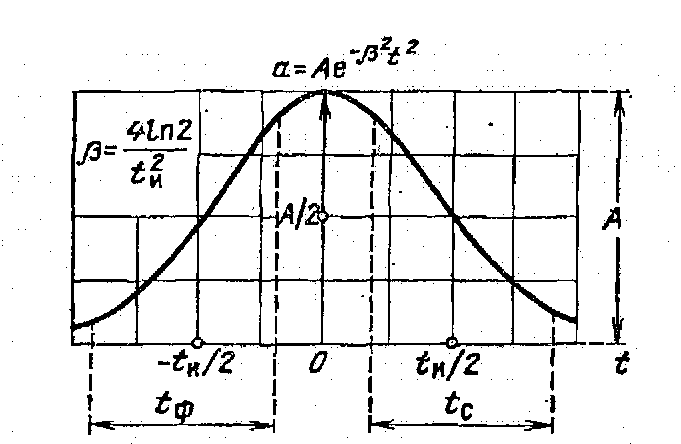
| Рис. 12. |
широко применяемой в теории вероятностей. Импульс такой формы играет особую роль в технике приема импульсных сигналов (в шумах): при таком импульсе смягчается проти-воречие между требованием сосредоточения энергии импульса во времени и требованием сосредоточения энергии импульса в спектре. Для сравнения укажем, что прямоугольный импульс наилучшим образом удовлетворяет первому требованию, но обладает чрезмерно широким спектром.
В соответствии с формулой (2.2), из условия (рис. 12)
находим (после логарифмирования) активную длительность
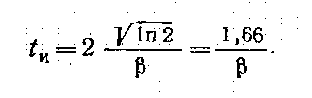(2.23)
Максимальная крутизна импульса, определяемая из условия d2a/dt2 = 0, соответствует моментам
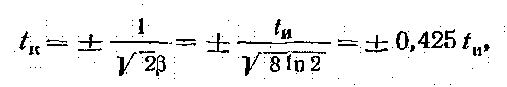(2.24)
где учтено соотношение (2.23). Подставляя значение t = tи в формулу (2.22), получим
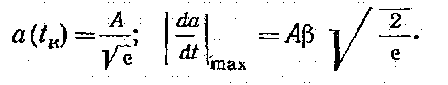(2.25)
Моменты ± t0,1 и ± t0,9, в которые величина импульса равна соответственно 0,1 А и 0,9 А, находятся из уравнений
Отсюда активные длительности фронта и среза импульса
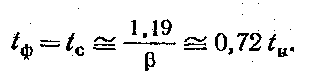(2.26)
АКТИВНАЯ ШИРИНА СПЕКТРА ИМПУЛЬСОВ
1. Основные характеристики импульсных сигналов выражаются через временные и
амплитудные параметры. Соответственно основной математический аппарат импульсной техники — аппарат интегро-дифференциальных уравнений, решаемых обычно операционным методом. Однако если импульсный процесс описывается дифференциальным уравнением высокого порядка, строгое или приближенное решение которого оказывается чрезмерно трудным или громоздким, то приходится прибегать к качественным спектральным представлениям. В таких случаях импульс той или иной
формы характеризуют активной шириной спектра (Δf)с, а цепь, подверженную действию импульса - шириной полосы пропускания (Δf)п. Затем устанавливают приближенное соотношение между (Δf)с и (Δf)п отвечающее требованиям конкретной задачи.
2. Известно, что основная энергия видео импульса сосредоточена в низкочастотной
части его энергетического спектра S2 = F(f) (рис. 17). При оперировании с «гладкими» (без существенного проявления наложенные паразитных колебаний) импульсами удовлетворительный результат качественного спектрального анализа получается в случае, если активная ширина спектра импульса определяется тем диапазоном частот от f = 0 до некоторой верхней частоты fв = (Δf)с, в котором сосредоточено 95% полной энергии импульса [ (Δf)с = (Δf)0,95 ].
| Рис. 17. |
