Обычно основное значение имеет не абсолютная величина ΔА, а относительная величина спада вершины, определяемая параметром
λA = ΔА/A. (2.1)
Иногда (например, при импульсной модуляции магнетрона) предъявляются жесткие требования к постоянству вершины импульса (λА ≤0,01 …0,05). В ряде случаев эти требования значительно смягчаются (λА ≤ 0,1). При формировании предельно коротких импульсов вообще не удается получать импульсы с уплощенной вершиной (трапецеидальный импульс вырождается в треугольный).
4.Активная длительность импульса. Измерение длительности tи0 импульса становится малоопределенным при оперировании с реальными импульсами (см. п. 5). Кроме того, основной результат воздействия импульса на то или иное устройство
проявляется после того, как величина импульса достигнет некоторого уровня; этот уровень обычно близок к 50% от высоты импульса. Из этих соображений введено понятие об активной длительности tи импульса, измеряемой на уровне 0,5А (рис. 2):
tи = t”0.5 - t’0.5 (2.2)
| Рис. 2. |
В общем случае tи < tи0. Равенство tи = tи0 справедливо для прямоугольного импульса. У треугольного импульса tи = 0,5tи0.
5.Активные длительности фронта и среза импульса. Реально получаемые импульсы не отличаются остротой и геометрической простотой формы, свойственной импульсам идеализированной формы (см. рис.1). На рис. 3 представлен примерный вид реально получаемого импульса трапецеидальной формы. Определение длительностей фронта tф0 и среза tc0 (а также и длительности tи0) при показанной на рис. 3 сглаженной форме импульса становится малоопределенным. Поэтому для характеристики формы реальных импульсов введено понятие об активных длительностях фронта и среза импульсов.
Активная длительность фронта tф и активная длительность среза tc определяются разностями соответствующих, моментов времени, в которые величина импульса а = a(t)
принимает значения а = 0,9A и а = 0,1A (рис. 3):
(2.3)
Интервалы времени, соответствующие tф и tc, называются междецильными интервалами.
| Рис. 3. Рис. 4. |
6. На практике приходится оперировать с импульсами, у которых хотя и проявляется уплощенный характер вершины, но спад вершины ΔА > 0,1 A (рис.4). Кроме того, иногда после среза импульса образуется послеимпульсный обратный выброс на полярности, противоположной полярности основной части импульса, причем
величина выброса Aв- > 0,1А, т. е. она достаточно существенна. Эту часть импульса называют хвостом импульса; длительность tx0 хвоста импульса определяет в ряде устройств длительность стадии восстановления, т. е. длительность возвращения устройства к исходным начальным условиям, с чем связана его готовность к последующему нормальному действию.
При оперировании с импульсом, изображенным на рис. 4, определение активной длительности среза указанным в п. 5 путем становится невыразительным. Кроме того, рабочее назначение среза импульса при его воздействии на то или иное устройство связано с п е ре п а д о м величины импульса (при срезе)
(2.4)
не равным в общем случае высоте А импульса. Поэтому целесообразно определять активную длительность среза из построения, приведенного на рис 4. Именно, находится точка С (точка пересечения касательных к вершине импульса и к его срезу) и вычисляется величина ΔАс; затем находятся точки М и N (определяемые величиной 0,1 ΔАс) и соответствующие им моменты времени tM и tN, после чего определяется активная длительность среза tс = tN — tM.
7. В ряде случаев практики важна достаточно точная фиксация моментов t1 или t2
(рис. 5), в которые величина импульса напряжения (на фронте или срезе) равна некоторому пороговому значению U пор. Из-за нестабильности источников питания или в результате смены электронного прибора величина порогового напряжения меняется в некоторых пределах (от U пор до U'nop). Это приводит к вариации моментов t1 и t2 в соответствующих пределах (Δ t1 = t’1 — t1 и Δ t2 = t2 — t’2). Такие же последствия получаются и при изменении высоты U импульса.
| Рис. 5. Рис. 6. |
При прямоугольном импульсе описанной выше вариации моментов t1 или t2 не
происходило бы. Чем меньше длительность фронта (среза), тем меньше временная нестабильность работы импульсных устройств. Поэтому обычно предъявляются определенные требования к длительности фронта или среза импульса. Эти требования в зависимости от назначения определяются равенствами:
tф ≈ (0,1…0,3)tи; tс ≈ (0,1…0,3)tи. (2.5)
8. Из-за влияния паразитных элементов импульсных устройств на вершине и хвосте импульса иногда заметно проявляются нежелательные для многих применений наложенные паразитные колебания (рис. 6). Благоприятно то, что благодаря наличию в рабочих цепях устройств активных сопротивлений паразитные колебания довольно быстро затухают. Для ускорения затухания иногда специально вводят активные элементы в рабочие цепи устройств.
В ряде технических применений (в частности, в телевидении) предъявляются определенные требования к равномерности вершины импульса, нарушаемой паразитными колебаниями. Неравномерность вершины оценивается относительной величиной Ав выброса импульса (рис. 6); аналогично оценивается значимость обратного выброса Ав-:
(2.6)
Выброс импульса определяет пиковое значение импульса Aп = А + Ав. Но высота А импульса, выражающая его номинальную величину, обычно определяется без учета паразитных колебаний на вершине.
9. Основные параметры последовательности импульсов. Наиболее важными являются три связанных между собой параметра: период ТП повторения импульсов, скважность следования импульсов QС = T П /tи и частота повторения импульсов
(2.7)
Частота повторения импульсов определяет число импульсов в 1 с; она измеряется в герцах {мегагерцах); 1 Гц — частота повторения, соответствующая 1 импульсу в I с.
10. Последовательность импульсов характеризуется также своим средним и действующим значениями, зависящими от формы импульсов и, в особенности, от скважности их следования. Определим эти значения для периодической последовательности импульсов, причем будем полагать, что a (t) — аналитическое выражение одного из импульсов последовательности на интервале (0 … Tп).
Средним значением последовательности импульсов, определяющим постоянную составляющую импульсного процесса, называется величина
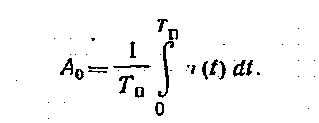(2.8)
Для последовательности прямоугольных импульсов высотой А
(2 8а)
Действующее (эффективное) значение последовательности импульсов находится из равенства энергий
(2.9)
где k — коэффициент пропорциональности. Для последовательности прямоугольных импульсов высотой А из равенства (2.9) получаем
А2tи = А2эТп.
откуда
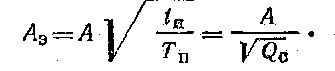(2.9а).
Из сопоставления формул (2.8а) и (2.9а) следует, что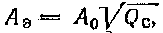 
т. е. действующее значение импульсного процесса больше его среднего значения, причем это различие повышается с возрастанием скважности следования импульсов.
