Цепь переменного тока с емкостью и активным сопротивлением. Векторные диаграммы. Фазовые соответствия между токами и напряжениями

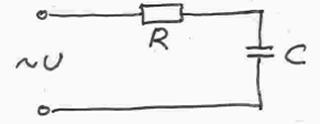
В реальных цепях переменного тока с ёмкостью всегда имеется активное сопротивление-сопротивление проводов, активные потери в конденсаторе и т.д.. Поэтому реальную цепь с ёмкостью следует рассматривать состоящей из последовательно соединённых активного сопротивления R и конденсатора C.

Через конденсатор и резистор протекает один и тот же ток I = Iо∙sinωt,

поэтому в качестве основного выберем вектор тока и будем строить вектор напряжения, приложенного к этой цепи.

Напряжение, приложенное к цепи, равно век-ой сумме падений напряжений на конденсаторе и на резисторе: U = Uc + 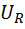(*векторно)

Напряжение на резисторе будет совпадать по фазе с током:

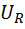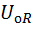= ∙sinωt, а напряжение на конденсаторе будет отставать по фазе от тока на угол π / 2:

Uc = Uоc∙sin(ωt - π/2)

Построим векторы I, 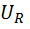и Uc и, воспользовавшись формулой, найдём вектор U.

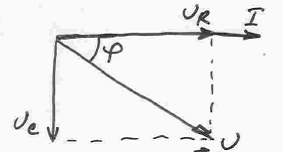Из векторной диаграммы следует, что в рассматриваемой цепи ток I опережает по фазе приложенное напряжение U, но не на π/2, как в случае чистой ёмкости, а на угол φ. Этот угол может изменяться от 0 до π/2 и при заданной ёмкости С зависит от значения активного сопротивления: с увеличением R угол φ уменьшается.

Модуль вектора U равен:

U = 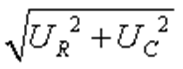= I 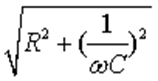= I∙Z,где

Z = 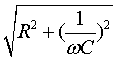называется полным сопротивлением цепи.

Сдвиг по фазе между током и напряжением:

tgφ = Uc/ 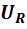= (1/ωC)/R = 1/(ω∙R∙C)

16. Последовательная цепь переменного тока. Резонанс напряжений. Рассмотрим цепь переменного тока, содержащую индуктивность, ёмкость и резистор, соединённые последовательно.

Рис.4.24. Последовательная цепь переменного тока.

 

Через все эти элементы протекает один и тот же ток, поэтому в качестве основного выберем вектор тока, и будем строить вектор напряжения, приложенного к этой цепи.

U = U_L + U_c + U_R

Мы знаем, что напряжение на резисторе совпадает по фазе с током, напряжение на катушке опережает ток по фазе на π⁄2, а напряжение на ёмкости отстаёт от тока по фазе на π⁄2. Запишем эти напряжения в следующем виде:

U_R = U_mR∙sinωt = I_m∙R∙sinωt

U_L = U_mL∙sin(ωt + π/2) = I_m∙ω∙L∙sin(ωt + π/2)

U_c = U_mc∙sin(ωt - π/2) = (I_m/ωC)∙sin(ωt - π/2)

Построим векторную диаграмму и найдём вектор U.

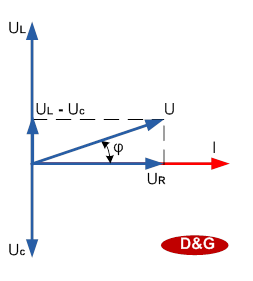
Рис.4.25. Векторная диаграмма для последовательной цепи переменного тока.

Из этой диаграммы находим модуль вектора приложенного к цепи напряжения и сдвиг фаз φ между током и напряжением:

U = = I·Z, где

Z = , называется полным сопротивлением цепи.

Из векторной диаграммы tgφ = (U_L - U_c)/U_R = .

Разность фаз между током и напряжением определяется соотношением векторов U_L, U_c и U_R. При U_L - U_c > 0 угол φ положительный и нагрузка имеет индуктивный характер. При U_Lменьше U_c угол отрицательный и нагрузка имеет ёмкостной характер. См. рис.4.26, а при U_L = U_c нагрузка имеет активный характер.

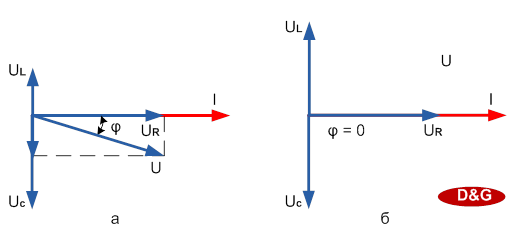
Рис. 4.26. Векторная диаграмма последовательной цепи:

а - нагрузка имеет ёмкостной характер; б - нагрузка имеет активный характер.

Разделив стороны треугольника напряжений на значение тока в цепи, получим треугольник сопротивлений (рис. 4.27), в котором R - активное сопротивление, Z - полное сопротивление, а X = X_L - X_c - реактивное сопротивление.

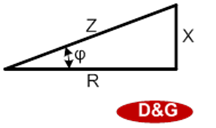
Рис.4.27. Треугольник сопротивлений.

Кроме того, R = Z∙cosφ; X = Z∙sinφ.

Когда напряжения на индуктивности и ёмкости, взаимно сдвинутые по фазе на 180 градусов, равны по величине, то они полностью компенсируют друг друга (рис.4.26, б).

Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, а ток в цепи совпадает по фазе с напряжением. Этот случай называется резонансом напряжений.

Условие резонанса напряжений:

U_L = Uc, а значит и X_L = X_c или ω_о = 1/ ω_о∙С, где

ωо - угловая частота резонанса. Ток в цепи равен:

I = U / = U/R

Ток в цепи при этом достигает максимального значения, φ = 0, а cosφ = 1. Резонанс напряжений характеризуется обменом энергии между магнитным полем катушки и электрическим полем конденсатора. Увеличение магнитного поля катушки индуктивности происходит за счёт уменьшения энергии электрического поля в конденсаторе и наоборот. При резонансе напряжений напряжения на реактивных сопротивлениях XL и Хс могут заметно превышать приложенное к цепи напряжение.

U / U_L = I∙Z / I∙X_L = Z / X_L или U∙L = U∙(X_L / R), т.е. напряжение на индуктивности будет больше приложенного напряжения в X_L/R раз. Это означает, что на отдельных участках цепи могут возникать опасные напряжения.

Вернёмся к формуле (4.31).

ω_о∙L = 1 / (ωо∙С);

ω²_о∙L∙С = 1;

ωо = 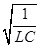= , но ω = 2πf, значит 2πf_о = , тогда

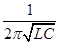fо = , где

f_о - частота при резонансе напряжений в герцах;

L - индуктивность в генри;

С - ёмкость в фарадах.