Система линейных уравнений с двумя переменными. Решение систем линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений.
Цель - познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умение решать системы линейных уравнений с двумя переменными и применять их при решении задач.
Знать, что такое линейное уравнение с двумя переменными, система уравнений, знать различные способы решения систем линейных уравнений с двумя переменными: способ подстановки и способ сложения; понимать, что уравнение - это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.
Уметь правильно употреблять термины: " уравнение с двумя переменными", "система"; понимать в тексте, в речи учителя, понимать формулировку задачи "решить систему линейных уравнений с двумя переменными"; строить некоторые графики уравнений с двумя переменными; решать системы линейных уравнений с двумя переменными различными способами.
Повторение. Решение задач (6 ч)
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).
Геометрия 7 класс
Начальные геометрические сведения (12 ч)
Простейшие геометрические фигуры. Сравнение и измерение отрезков и углов. Понятие о перпендикулярных прямых, смежных и вертикальных углах.
Цель - закрепить и расширить знания, полученные ранее по начальным геометрическим сведениям. Познакомиться с понятием теоремы и ее доказательством.
Знать определение прямой, отрезка, луча, угла и его видов, полуплоскости; понятие равных фигур, перпендикулярных прямых и отрезков; что называется серединой отрезка, градусной мерой угла; определение смежных и вертикальных углов.
Уметь использовать символическую запись, изображать и распознавать простейшие фигуры на чертежах; формулировать и обосновывать утверждения о свойствах смежных и вертикальных углов, доказывать теоремы о существовании и единственности перепендикуляра к прямой; решать задачи на доказательства и вычисления.
Треугольники (29 ч)
Равнобедренный треугольник. Признаки равенства треугольников. Прямоугольные треугольники. Соотношения между сторонами и углами треугольника.
Цель - повторить и закрепить знания по треугольникам и их видам.
Знать определение треугольника и его составляющие элементы, периметра, медианы, биссектрисы и высоты, равнобедренного и прямоугольного треугольника; в чем состоит метод доказательства от противного.
Уметь формулировать и доказывать теоремы, связанные с признаками равнобедренного треугольника; объяснить, какие треугольники называются равными и уметь доказывать соответствующие теоремы; доказывать свойство биссектрисы, медианы и высоты треугольника, а также теорему о неравенстве треугольника и сумме углов треугольника.
Окружность (20 ч)
Отрезки и углы, связанные с окружностью. Задачи на построение.
Цель - повторить, закрепить и расширить знания по окружности.
Знать определение окружности и связанных с ней понятий (центр, радиус, диаметр, хорда, дуга, центральный и вписанный угол, касательная к окружности, градусная мера дуги); что такое задачи на построение.
Уметь исследовать и изображать взаимное расположение прямой и окружности; формулировать и доказывать теоремы о свойстве касательной, об угле между касательной и хордой, о вписанном угле; решение задач на построение.
Повторение. Решение задач (7 ч)
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс геометрии 7 класса).
Алгебра 8 класс
Рациональные дроби (23 ч)
Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление дробей. Преобразование рациональных выражений. Функция 
и ее график.
Цель - выработать умение выполнять тождественные преобразования рациональных выражений.
Знать основное свойство дроби, рациональные дробные выражения; правильно употреблять термины "выражение", "тождественное преобразование", понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь.
Знать и понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь, свойства обратной пропорциональности.
Уметь осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления, выполнять действия сложения и вычитания с алгебраическими дробями, сокращать дробь, выполнять разложение многочлена на множители применением формул сокращенного умножения, выполнять преобразование рациональных выражений, осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления, выполнять действия умножения и деления с алгебраическими дробями, возводить дробь в степень, выполнять преобразование рациональных выражений; правильно употреблять функциональную терминологию (значение функции, аргумент, график функции), строить график обратной пропорциональности, находить значение функции 
по графику, формуле.
Квадратные корни (19 ч)
Понятие об иррациональном числе. Общие сведения о действительном числе. Квадратный корень, приближенное значение квадратного корня. Свойства квадратных корней. Преобразование выражений, содержащих квадратные корни. Функция 
и ее график.
Цель - систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие числа; выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни.
Знать определения квадратного корня, арифметического квадратного корня, рационального и иррационального числа, обозначение множества рациональных чисел; свойства арифметического квадратного корня.
Уметь выполнять преобразование числовых выражений, содержащих квадратные корни; решать уравнение вида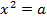 
; находить приближенные значения квадратного корня; находить квадратный корень из произведения, дроби, степени, строить график функции и находить значения этой функции по графику или по формуле; выносить множитель из-под знака корня, вносит множитель под знак корня; выполнять преобразование выражений, содержащих квадратные корни.
