Определение. Внутренней энергией какого-либо тела называется энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Она является функцией внутреннего состояния системы. Для идеального газа внутренняя энергия состоит из суммы энергий поступательного, вращательного и колебательного движений молекул. (Заметим, что в общем случае во внутреннюю энергию входят энергия взаимодействия атомов, энергия электронных оболочек, внутриядерная энергия и др.). Внутреннюю энергию одного моля идеального газа найдём, умножив число Авогадро на среднюю энергию одной молекулы:

Учитывая, что  , получим:
, получим:

|
т.е. внутренняя энергия идеального газа является функцией температурыи пропорциональна ей, а также зависит от числа степеней свободы молекул. То, что внутренняя энергия является функцией состояния системы, означает, что всякий раз, когда система оказывается в данном состоянии, ее внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе системы из одного состояния в другое будет всегда равно разности значений внутренней энергии в этих состояниях, независимо от пути, по которому совершался переход.
Свяжем внутреннюю энергию с теплоёмкостью. По определению теплоёмкость в процессе при постоянном объёме 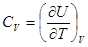 , для идеального газа
, для идеального газа

|
Соответственно

|
3. Основное уравнение молекулярно-кинетической теории.
Постановка задачи. Требуется получить связь между макропараметрами – давлением P, температурой T, с микропараметрами – массой молекулы m, её скоростью  и концентрацией молекул n.
и концентрацией молекул n.
Пусть имеется некоторый сосуд с газом. Будем считать, что молекулы могут двигаться вдоль осей x, y, z. Выберем на стенке сосуда участок поверхности  (Рис. 7.2). Если в сосуде N молекул, то вследствие равновероятности этих направлений вдоль каждой оси будет двигаться
(Рис. 7.2). Если в сосуде N молекул, то вследствие равновероятности этих направлений вдоль каждой оси будет двигаться 

| молекул. Половина из них движется вдоль данного направления, т.е.  (ось имеет два направления).
Предположим, что все молекулы движутся с одинаковой скоростью, равной
(ось имеет два направления).
Предположим, что все молекулы движутся с одинаковой скоростью, равной  . Тогда за время . Тогда за время  до элемента стенки до элемента стенки  долетят молекулы, заключённые в объёме параллелепипеда с основанием долетят молекулы, заключённые в объёме параллелепипеда с основанием  и высотой и высотой   . Число этих молекул равно . Число этих молекул равно
|
| Рис. 7.2 |
произведению плотности молекул  (где
(где  объём сосуда) на объём
объём сосуда) на объём 
 , т.е. число молекул, летящих к площади
, т.е. число молекул, летящих к площади
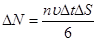 (1)
(1)
По закону сохранения импульса каждая молекула при ударе о стенку передаёт ей импульс (удар считается упругим), равный изменению импульса молекулы (Рис. 7.3, а, б).

 . (2)
. (2)
По 2-му закону Ньютона:
 , (3)
, (3)
где  сила, действующая со стороны молекулы на стенку;
сила, действующая со стороны молекулы на стенку;  длительность взаимодействия молекулы со стенкой.
длительность взаимодействия молекулы со стенкой.
Для всех молекул, находящихся в параллелепипеде:

|  , где , где
 средняя сила, с которой молекулы действуют на стенку средняя сила, с которой молекулы действуют на стенку  . Учитывая соотношение (3): . Учитывая соотношение (3):
 ,
подставляя (1) и (2) в последнее соотношение, получим: ,
подставляя (1) и (2) в последнее соотношение, получим:
| ||||
| рис. 7.3 |
 .
.
Поделив правую и левую части на  , учитывая, что
, учитывая, что
по определению давления  и производя необходимые сокращения, получим
и производя необходимые сокращения, получим  или
или  .
.
Если в выводе учесть, что скорости отдельных молекул могут быть различными, то величину  следует заменить средней величиной квадрата скорости
следует заменить средней величиной квадрата скорости 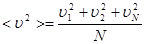 .
.
А так как средняя энергия поступательного движения молекулы
 ,
,
то

| Основное уравнение молекулярно-кинетической теории. |
Физический смысл уравнения: давление, оказываемое газом на стенки сосуда прямо пропорциональна числу молекул в единице объёма и средней кинетической энергии поступательного движения одной молекулы.
4. Уравнение состояния идеального газа Клапейрона-Менделеева
(Клапейрон (1799 – 1864) – французский физик и инженер; Менделеев Дмитрий Иванович (1834 – 1907) – великий русский учёный). Опыт даёт, что при небольших плотностях газы подчиняются уравнению (Клапейрона):
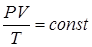 .
.
В соответствии с законом Авогадро моли всех газов занимают при одинаковых условиях одинаковый объём.
Отсюда const будет одинакова для всех газов, если количество равно 1 молю. Обозначив const=R, получим (Менделеев):
Уравнение состояния идеального газа для одного моля, где газовая постоянная  , а
, а  - объем 1 моля газа.
- объем 1 моля газа.

|
Если у нас имеется  молей, то объём будет
молей, то объём будет  ,
,  , подставим в уравнение состояния для 1-го моля:
, подставим в уравнение состояния для 1-го моля:
 или
или 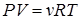 .
.
Количество вещества  можно представить в виде отношения массы газа m к молярной массе газа М
можно представить в виде отношения массы газа m к молярной массе газа М  и окончательно уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) для массы газа m:
и окончательно уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) для массы газа m:
 (4)
(4)
Следствие из уравнения Клапейрона-Менделеева. Газовую постоянную выразим как 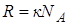 . Произведение
. Произведение  , тогда
, тогда 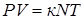 . Разделим обе части последнего уравнения на V и, учитывая, что
. Разделим обе части последнего уравнения на V и, учитывая, что
 концентрация молекул, получим
концентрация молекул, получим
 (5)
(5)
Оба уравнения (4) и (5) представляют различные формы записи уравнения состояния идеального газа. Это уравнение позволяет достаточно просто оценить параметры газа, если его можно считать идеальным.
5. Уравнение Ван-дер-Ваальса
(голландский физик, 1837 - 1923)
Ван-дер-Ваальс ввёл поправки в уравнение состояния идеального газа, учитывающие силы взаимодействия между молекулами и их собственный объём. Из уравнения Клапейрона – Менделеева для 1 моля  следует, что при
следует, что при 
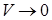 . Учтём в уравнении ограниченную сжимаемость газа. Заменим
. Учтём в уравнении ограниченную сжимаемость газа. Заменим  на
на  , где b – некоторая константа, учитывающая размеры молекул. Теперь при
, где b – некоторая константа, учитывающая размеры молекул. Теперь при 
 , т.е. смысл поправки b – это объём, к которому стремится моль газа при наиболее «плотной упаковке» молекул, а уравнение состояния с этой поправкой
, т.е. смысл поправки b – это объём, к которому стремится моль газа при наиболее «плотной упаковке» молекул, а уравнение состояния с этой поправкой  .
.
Учтём взаимодействие молекул. Сила взаимодействия между двумя элементарными объёмами пропорциональна плотности молекул, заключённых в одном и другом объёмах  . Плотность – величина, обратная объёму, занимаемому молекулами.
. Плотность – величина, обратная объёму, занимаемому молекулами.  . Отсюда поправка на взаимодействие молекул
. Отсюда поправка на взаимодействие молекул  , где a – некоторая константа, характеризующая силы молекулярного притяжения. В результате уравнение состояния одного моля реального газа приняло вид:
, где a – некоторая константа, характеризующая силы молекулярного притяжения. В результате уравнение состояния одного моля реального газа приняло вид:

|
Это и есть уравнение Ван-дер-Ваальса. Здесь a и b – постоянные Ван-дер-Ваальса, для разных газов они имеют свои значения.
Заметим, что поправка  имеет размерность давления, и её часто называют внутренним давлением. На стенку сосуда такой газ оказывает давление Р, однако, если бы силы притяжения между молекулами мгновенно исчезли, то давление на стенку стало бы
имеет размерность давления, и её часто называют внутренним давлением. На стенку сосуда такой газ оказывает давление Р, однако, если бы силы притяжения между молекулами мгновенно исчезли, то давление на стенку стало бы  , т.е. при переходе от идеального газа к реальному давление на стенку уменьшается – из-за сил притяжения между молекулами. Поправка b связана с собственным объёмом молекул и её размерность
, т.е. при переходе от идеального газа к реальному давление на стенку уменьшается – из-за сил притяжения между молекулами. Поправка b связана с собственным объёмом молекул и её размерность 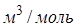 .
.
Изотермы реального газа
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса – кривые зависимости  от
от 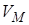 при заданных температурах Т, определяемые уравнением Ван-дер-Ваальса для 1 моля газа (рис. 9.2). Эти кривые рассматриваются для четырёх различных температур. При высоких температурах
при заданных температурах Т, определяемые уравнением Ван-дер-Ваальса для 1 моля газа (рис. 9.2). Эти кривые рассматриваются для четырёх различных температур. При высоких температурах  изотерма реального газа отличается от изотермы идеального газа только некоторым искажением её формы, оставаясь монотонно спадающей кривой. При некоторой температуре
изотерма реального газа отличается от изотермы идеального газа только некоторым искажением её формы, оставаясь монотонно спадающей кривой. При некоторой температуре 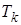 на изотерме имеется точка перегиба К. Эта изотерма называется критической, соответствующая ей температура
на изотерме имеется точка перегиба К. Эта изотерма называется критической, соответствующая ей температура 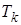 – критической температурой, а точка К – критической точкой. Состояние с критическими параметрами
– критической температурой, а точка К – критической точкой. Состояние с критическими параметрами  называется критическим состоянием.
называется критическим состоянием.

|
| Рис. 9.2 |
При температурах  изотермы имеют волнообразный участок. У реальных изотерм такого завитка нет, вместо него у них имеется прямолинейный горизонтальный участок (на рис. 9.2 обозначены пунктиром). Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая, ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму P, V под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар Ж+П), слева от неё находится область жидкого состояния (Ж), а справа – область пара (П). Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращён в жидкость ни при каком давлении.
изотермы имеют волнообразный участок. У реальных изотерм такого завитка нет, вместо него у них имеется прямолинейный горизонтальный участок (на рис. 9.2 обозначены пунктиром). Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая, ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму P, V под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар Ж+П), слева от неё находится область жидкого состояния (Ж), а справа – область пара (П). Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращён в жидкость ни при каком давлении.
6.
Характеристика жидкого состояния. Жидкое состояние, занимает промежуточное положение между газами и кристаллами, сочетает в себе некоторые черты обоих этих состояний. Для кристаллического состояния характерно упорядоченное расположение частиц (атомов или молекул), в газах в этом смысле полный хаос. Согласно рентгенографическим исследованиям, в отношении характера расположения частиц жидкости занимают промежуточное положение.
В расположении частиц жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой частице расположение ближайших к ней соседей является упорядоченным. Однако по мере удаления от данной частицы расположение по отношению к ней других частиц становится всё менее упорядоченным и довольно быстро порядок в расположении частиц полностью исчезает.
В кристаллах имеет место дальний порядок – упорядоченное расположения частиц по отношению к любой частице наблюдается в пределах значительного объёма.
Оценить структуру вещества позволяет радиальная функция распределения (в некоторых учебниках она называется парной функцией распределения). Выберем некоторую молекулу в качестве тела отсчёта. Среднее число молекул в сферическом слое объёмом  , находящихся на расстоянии r от выбранной молекулы (Рис. 10.1) обозначим dN(r). Вероятность обнаружить молекулы в этом сферическом слое
, находящихся на расстоянии r от выбранной молекулы (Рис. 10.1) обозначим dN(r). Вероятность обнаружить молекулы в этом сферическом слое

|  , где N – общее число молекул в некотором рассматриваемом объёме V, g(r) – радиальная функция распределения. В , где N – общее число молекул в некотором рассматриваемом объёме V, g(r) – радиальная функция распределения. В
|
| Рис. 10.1 |
случае идеального газа никакие элементы объёма не имеют преимущества и вероятность нахождения частицы в данном объёме пропорционально объёму и g(r)= 1.
В идеальном кристалле структура жёсткая и все взаимные расстояния являются фиксированными (Рис. 10.2).

| Говорят, что в идеальном газе вообще нет порядка, а в кристалле – дальний порядок – на любом расстоянии от данного атома находится строго определённое количество других атомов, располагающихся друг относительно друга строго определённо. Радиальные функции распределения для кристаллов и идеального газа представлены на рис. 10.3. |
| Рис. 10.2 |
Пики соответствует узлам решётки, а конечная ширина линии g(r) является следствием колебаний атомов относительно узла в реальном кристалле.

| Заметим, что для кристалла  зависит не только от модуля вектора зависит не только от модуля вектора  , но и от его направления. В некотором другом направлении пики могут находится на других расстояниях. Для жидкостей функция , но и от его направления. В некотором другом направлении пики могут находится на других расстояниях. Для жидкостей функция  представлена на рис. 10.4. На малых расстояниях поведение подобно кристаллам (пики чередуются, но представлена на рис. 10.4. На малых расстояниях поведение подобно кристаллам (пики чередуются, но
|
| Рис. 10.3 |
более сглажены, чем у кристалла). На дальних расстояниях кривая  стремится к 1 как для идеального газа.
стремится к 1 как для идеального газа.

| В жидкостях с удлиненными молекулами наблюдается взаимная ориентация молекул в пределах значительного объёма, чем обуславливается анизотропия оптических и некоторых других свойств. Такие жидкости получили название жидких кристаллов. У них |
| Рис. 10.4 |
упорядочена только ориентация, взаимное же расположение, как и в обычных жидкостях, дальнего порядка не обнаруживает.
7. Поверхностное натяжение.
Молекулы жидкости располагаются настолько близко друг к другу, что силы притяжения между ними имеют значительную величину. Взаимодействие быстро убывает с расстоянием, начиная с некоторого расстояния r (радиус молекулярного действия). На каждую молекулу, находящуюся в поверхностном слое толщиной r, будет действовать сила, направленная внутрь жидкости (Рис. 10.5).

| Переход молекулы из глубины жидкости в поверхностный слой связан с необходимостью совершения работы против действующих в поверхностном слое сил. Эта работа (за счёт кинетической энергии молекул) идёт |
| Рис. 10.5 |
на увеличение потенциальной энергии молекулы. То есть в поверхностном слое молекулы обладают дополнительной потенциальной энергией - поверхностной  .
.
Из-за наличия действующих на молекулы в поверхностном слое сил, направленных внутрь жидкости, жидкость стремится к сокращению своей поверхности, как если бы она была заключена в упруго растянутую плёнку, стремящуюся сжаться (никакой плёнки на самом деле нет).
Представим плёнку жидкости (например, мыльную плёнку), натянутую на проволочную рамку, одна из сторон которой (перемычка) может перемещаться (Рис. 10.6). Благодаря стремлению поверхности уменьшиться, на проволочку будет действовать сила. Она направлена по касательной к поверхности жидкости, перпендикулярно к участку контура 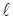 (длина перемычки), на который она действует (
(длина перемычки), на который она действует ( ).
).

| Сила поверхностного натяжения, приходящаяся на единицу длины участка контура 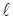 , называется коэффициентом поверхностного натяжения (размерность н/м).
Вследствие стремления поверхностного слоя к сокращению со стороны плёнки будет действовать на перемычку сила, равная , называется коэффициентом поверхностного натяжения (размерность н/м).
Вследствие стремления поверхностного слоя к сокращению со стороны плёнки будет действовать на перемычку сила, равная  . Чтобы перемычка находилась в равновесии, к ней нужно приложить внешнюю силу F, . Чтобы перемычка находилась в равновесии, к ней нужно приложить внешнюю силу F,
|
| Рис. 10.6 |
равную силе натяжения плёнки, т.е.  . Коэффициент 2 появляется из-за того, что плёнка имеет два поверхностных слоя.
. Коэффициент 2 появляется из-за того, что плёнка имеет два поверхностных слоя.
Жидкость вне поля внешних сил будет принимать форму с минимальной поверхностью, т.е. форму шара.
Давление под искривлённой поверхностью.
В случае искривлённой поверхности силы поверхностного натяжения стремятся сократить эту поверхность. (Рис. 10.7).

| Благодаря этим силам в жидкости возникает дополнительное давление  , а давление в жидкости , а давление в жидкости  , где , где  - -
|
| Рис. 10.7 |
давление в случае неискривлённой поверхности, причём  >0 в случае выпуклой поверхности, и
>0 в случае выпуклой поверхности, и  <0, если поверхность вогнутая (в этом случае поверхностный слой, стремится сократиться, растягивает жидкость и давление уменьшается).
<0, если поверхность вогнутая (в этом случае поверхностный слой, стремится сократиться, растягивает жидкость и давление уменьшается).
Вычислим дополнительное давление для сферической поверхности жидкости. Рассечём мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария. Из-за поверхностного натяжения

| оба полушария (Рис. 10.8) притягиваются друг к другу с силой:
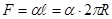 .
Эта сила прижимает друг к другу оба полушария по поверхности .
Эта сила прижимает друг к другу оба полушария по поверхности  и обуславливает дополнительное давление: и обуславливает дополнительное давление:
Лаплас обобщил эту формулу на поверхность любой формы. | |
| Рис. 10.8 |
Формула Лапласа выглядит так:

| |||

| Где  и и  – радиусы кривизны в двух взаимно перпендикулярных плоскостях, пересечение которых совпадает с нормалью к поверхности жидкости в интересующей нас точке (Рис. 10.9). Например, для поверхности цилиндрической формы один из радиусов кривизны стремится к – радиусы кривизны в двух взаимно перпендикулярных плоскостях, пересечение которых совпадает с нормалью к поверхности жидкости в интересующей нас точке (Рис. 10.9). Например, для поверхности цилиндрической формы один из радиусов кривизны стремится к  и и
 . .
| ||
| Рис. 10.9 | |||
Смачивание и капиллярные явления.
Смачивание – явление, возникающее при соприкосновении жидкости с поверхностью твёрдого тела или другой жидкости. Выражается, в частности, в растекании жидкости по твёрдой поверхности. Смачивание вызывает образование мениска в капиллярной трубке, определяет форму капли на твёрдой поверхности и др. (Заметим, что обычно смачивание рассматривают как результат межмолекурного взаимодействия, однако смачивание может быть результатом химической реакции, диффузионных процессов).
Мерой смачивания обычно служит краевой угол между касательными к поверхности жидкости. (Рис. 10.10). Если  , то говорят, что
, то говорят, что

| жидкость смачивает поверхность твёрдого тела. При 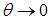 имеет место полное смачивание. Если имеет место полное смачивание. Если 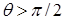 , то жидкость не смачивает поверхность. При , то жидкость не смачивает поверхность. При  мы имеем полное несмачивание. Условие равновесия элемента контура длиной мы имеем полное несмачивание. Условие равновесия элемента контура длиной  (расположен перпендикулярно плоскости рисунка 10.10 в т. А). (расположен перпендикулярно плоскости рисунка 10.10 в т. А).
|
| Рис. 10.10 |
 ,
,
где  коэффициенты поверхностного натяжения жидкости на границах: твёрдое тело – газ, твёрдое тело – жидкость, жидкость – газ. Сокращая на
коэффициенты поверхностного натяжения жидкости на границах: твёрдое тело – газ, твёрдое тело – жидкость, жидкость – газ. Сокращая на  , получим для краевого угла соотношение:
, получим для краевого угла соотношение:
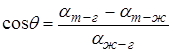
|
(Например, полное смачивание будет при  ).
).
Смачивание имеет важное значение в промышленности. Хорошее смачивание необходимо при крашении, стирке, обработке фотоматериалов, пайке. Примеси сильно сказываются на величине поверхностного натяжения. Например, растворение в воде мыла уменьшает её коэффициент поверхностного натяжения почти в 1,5 раза (что, в частности и обуславливает использование мыла в качестве моющего средства). Несмачивание может приводить к тому, что из решета, нити которого покрыты парафином (при небольшом уровне воды), вода не выливается, опровергая известную поговорку.
Капиллярные явления.
Существование смачивания и краевого угла приводит к тому, что вблизи стенок сосуда наблюдается искривление поверхности жидкости. Если жидкость смачивает стенки, поверхность имеет вогнутую форму, если не смачивает – выпуклую. Такого рода изогнутые поверхности жидкости называются мениском. (рис. 10.11)

| 
|
| Смачивание | Несмачивание |
| Рис. 10.11 |
Под искривлённой поверхностью в капилляре давление будет отличаться от давления под плоской поверхностью на величину  . Между жидкостью в капилляре и в широком сосуде устанавливается такая разность уровней
. Между жидкостью в капилляре и в широком сосуде устанавливается такая разность уровней  , чтобы гидростатическое давление
, чтобы гидростатическое давление  уравновешивало капиллярное давление
уравновешивало капиллярное давление  . В случае сферической формы мениска
. В случае сферической формы мениска
 . Радиус кривизны мениска выразим через краевой угол
. Радиус кривизны мениска выразим через краевой угол  и радиус капилляра r
и радиус капилляра r 
 , тогда
, тогда 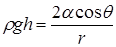 ,
,

|
В случае смачивания 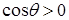 и высота поднятия жидкости в капилляре
и высота поднятия жидкости в капилляре  тем больше, чем меньше радиус капилляра r.
тем больше, чем меньше радиус капилляра r.
Капиллярное явление занимает в жизни человека исключительную роль. Снабжение влагой растений, деревьев происходит именно с помощью капилляров, которые есть в каждом растении. Капиллярные явления могут играть и отрицательную роль. Например, в строительстве. Необходимость гидроизоляции фундаментов зданий вызвана капиллярными явлениями.
8. Механизм пластической деформации. В основе пластического деформирования металлов лежит перемещение дислокаций. Сущностью пластического деформирования является сдвиг, в результате которого одна часть кристалла смещается по отношении к другой за счёт скольжения дислокаций. На рис. 11.7 (а, б, в) изображено движение краевой дислокации с образованием ступеньки единичного сдвига.

| 
| 
|
| а | б | в |
| Рис. 11.7 |
Заметим, что в действительности атомы перескакивают в новые положения небольшими группами поочерёдно. Такое поочерёдное перемещение атомов может быть представлено как перемещение дислокации. Дислокации служат причиной того, что пластическая деформация реальных кристаллов происходит под воздействием напряжений на несколько порядков меньших, чем вычисленных для идеальных кристаллов. Но если плотность дислокаций а также концентрация примесей велики, то это приводит к сильному торможению дислокаций и прекращению их движения. В результате, как ни парадоксально, прочность материала растёт.
Деформация растяжения. Закон Гука.
Характер изменения сил, связывающих атомы в твёрдом теле от расстояния между ними качественно такой же, как в газах и жидкостях (рис. 11.8). Если к стержню длиной 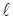 и сечением
и сечением  приложить силу
приложить силу  (рис. 11.9), то под действием этой силы стержень удлинится на некоторую величину
(рис. 11.9), то под действием этой силы стержень удлинится на некоторую величину  . При этом расстояния между соседними атомами вдоль оси стержня возрастут на некоторую величину
. При этом расстояния между соседними атомами вдоль оси стержня возрастут на некоторую величину  (рис. 11.8). Удлинение всей цепочки атомов
(рис. 11.8). Удлинение всей цепочки атомов  связано с
связано с  очевидным соотношением:
очевидным соотношением:

|  (*)
(где (*)
(где  – расстояние между соседними атомами при – расстояние между соседними атомами при  ). При смещении атомов из своих положений равновесия между ними возникают силы притяжения ). При смещении атомов из своих положений равновесия между ними возникают силы притяжения  , причём , причём  возрастает с увеличением возрастает с увеличением  : :
 .
Мысленно расчленим стержень на ряд параллельных цепочек атомов. Число цепочек на единицу площади .
Мысленно расчленим стержень на ряд параллельных цепочек атомов. Число цепочек на единицу площади
|
| Рис. 11.8 | |

| |
| Рис. 11.9 |
обозначим  . Тогда во всём стержне будет действовать суммарная сила:
. Тогда во всём стержне будет действовать суммарная сила:
 ,
,
причём  будет возрастать, пока
будет возрастать, пока  не уравновесит
не уравновесит  .
.

с учётом соотношения (*):
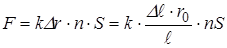 . (**)
. (**)
Разделим обе части на  , тогда
, тогда
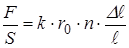 .
.
Отношение  – механическое напряжение деформации растяжения обозначим
– механическое напряжение деформации растяжения обозначим  . Произведение постоянных для данного материала величины
. Произведение постоянных для данного материала величины  обозначим
обозначим  (модуль Юнга). Отношение
(модуль Юнга). Отношение  обозначим
обозначим  (относительное удлинение). С учётом этих обозначений уравнение (**) приобретёт вид (одна из форм закона Гука)
(относительное удлинение). С учётом этих обозначений уравнение (**) приобретёт вид (одна из форм закона Гука) 

Закон Гука: относительное удлинение прямо пропорционально приложенному напряжению.
При 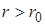 с увеличением
с увеличением 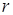 силы притяжения уменьшаются, и наступает разрыв.
силы притяжения уменьшаются, и наступает разрыв.
9.
Фазой называется макроскопическая физически однородная часть вещества, отделённая от остальных частей системы поверхностью раздела. Фазовое равновесие – одновременное существование фаз в многофазной системе (без изменения одной фазы за счет другой).
Разные фазы одного и того же вещества могут находиться в равновесии, соприкасаясь друг с другом. Такое равновесие наблюдается лишь в ограниченном интервале температур, причём каждому значению температуры  соответствует своё значение давления
соответствует своё значение давления  , при котором возможно равновесие. Совокупность состояний равновесия 2-х фаз изображается на диаграмме
, при котором возможно равновесие. Совокупность состояний равновесия 2-х фаз изображается на диаграмме  линией
линией  . Три фазы одного и того же вещества (твёрдая, жидкая и газообразная или жидкая и две твёрдых или три твёрдых) могут находиться в равновесии только при единственных значениях температуры и давления, которые на диаграмме
. Три фазы одного и того же вещества (твёрдая, жидкая и газообразная или жидкая и две твёрдых или три твёрдых) могут находиться в равновесии только при единственных значениях температуры и давления, которые на диаграмме  соответствует точка, называемая тройной.
соответствует точка, называемая тройной.
В термодинамике доказывается, что равновесие более чем 3-х фаз одного и того же веществаневозможно (и это подтверждено экспериментально).
Диаграмма состояния. (рис. 12.1)

| 1-2-3 переход кристалл  жидкость жидкость  газ
4-5 кристалл газ
4-5 кристалл  газ
6-7 переход из жидкости в газ без расслоения на фазы. газ
6-7 переход из жидкости в газ без расслоения на фазы.
|
| Рис. 12.1 |
Определение. Сублимация (возгонка) – непосредственный (без плавления) переход из кристаллического состояния в газообразное.
Из диаграммы (рис. 12.1) следует, что жидкая фаза может находиться в равновесии при давлениях не меньше, чем давление в тройной точке  . Например, в случае углекислоты (
. Например, в случае углекислоты (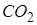 )
)  =5,11 атм, поэтому при атмосферном давлении (1 атм.) углекислота может существовать только в твёрдом и газообразном состояниях. Твёрдая углекислота (называемая сухим льдом) на воздухе сублимирует, а не тает (переход 4-5). Для большинства же обычных веществ
=5,11 атм, поэтому при атмосферном давлении (1 атм.) углекислота может существовать только в твёрдом и газообразном состояниях. Твёрдая углекислота (называемая сухим льдом) на воздухе сублимирует, а не тает (переход 4-5). Для большинства же обычных веществ  значительно меньше атмосферного давления (например, для
значительно меньше атмосферного давления (например, для 
 =4,58 мм. рт. ст.), поэтому переход из кристаллического состояния в газообразное осуществляется через жидкую фазу.
=4,58 мм. рт. ст.), поэтому переход из кристаллического состояния в газообразное осуществляется через жидкую фазу.
Кривая испарения заканчивается в критической точке К. Поэтому возможен процесс в обход критической точки К. в этом случае переход из жидкого состояния в газообразное совершается непрерывно (процесс  ) без расслаивания на две фазы. При температурах выше критической вещество не может быть сжижено никаким сжатием.
) без расслаивания на две фазы. При температурах выше критической вещество не может быть сжижено никаким сжатием.
Фазовые переходы с поглощением или выделением скрытой теплоты перехода называются фазовыми переходами первого рода. Например, в процессах плавления или кристаллизации. Фазовые переходы, не связанные со скрытой теплотой перехода, называются фазовыми переходами второго рода. Например, переход парамагнетик – ферромагнетик.
Уравнение Клапейрона – Клаузиуса
(без вывода).

|
 теплота фазового перехода,
теплота фазового перехода, 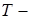 температура,
температура,  и
и  объёмы обеих фаз. (
объёмы обеих фаз. ( и
и  ,
,  относятся к одному и тому же количеству вещества, например, к 1 молю или 1 кг, т.е. является удеальными).
относятся к одному и тому же количеству вещества, например, к 1 молю или 1 кг, т.е. является удеальными).
 определяет наклон фазовой кривой фазового равновесия Р(Т). Уравнение Клапейрона – Клаузиуса даёт изменение температуры фазового перехода при изменении давления.
определяет наклон фазовой кривой фазового равновесия Р(Т). Уравнение Клапейрона – Клаузиуса даёт изменение температуры фазового перехода при изменении давления.
Пример. Для воды (льда) теплота плавления  . Разница удельных объёмов льда и воды при 0
. Разница удельных объёмов льда и воды при 0 

 (легко найти из соответствующих плотностей).
(легко найти из соответствующих плотностей).

 . То есть, с увеличением давления на одну атмосферу точка плавления льда понижается примерно на 0,0075 град.
. То есть, с увеличением давления на одну атмосферу точка плавления льда понижается примерно на 0,0075 град.
Опыт. Если на брусок льда, лежащий своими концами на неподвижных опорах, накинуть проволочную петлю, и к ней подвесить тяжёлый груз, то лёд под проволокой плавится. Вода выдавливается из-под проволоки и замерзает над ней. Проволока постепенно проходит через брусок, однако брусок остаётся неразрезанным.
10. Основные термодинамические понятия
Термодинамика в отличие от молекулярно-кинетической теории не вдаётся в рассмотрение микроскопической картины явлений (оперирует с макропараметрами). Термодинамика рассматривает явления, опираясь на основные законы (начала), которые являются обобщением огромного количества опытных данных.
Внутренняя энергия – энергия физической системы, зависящая от её внутреннего состояния. Внутренняя энергия включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т.д.) и энергию взаимодействия этих частиц. Кинетическая энергия движения системы как целого и её потенциальная энергия во внешних силовых полях во внутреннюю энергию не входит. В термодинамике и её приложениях представляет интерес не само значение внутренней энергии, а её изменение при изменении состояния системы. Внутренняя энергия – функция состояния системы.
Работа термодинамической системы над внешними телами заключается в изменении состояния этих тел и определяется количеством энергии, передаваемой системой внешним телам при изменении объема.

| Работа в термодинамике не является полным дифференциалом (не является функцией состояния, а зависит от пути) и обозначается  .
Для того чтобы изменить объём, занимаемый газом, надо совершить работу. Представим себе газ, заключённый в цилиндрический объём с поршнем, движением которого изменяется объём газа (рис. 14.1). .
Для того чтобы изменить объём, занимаемый газом, надо совершить работу. Представим себе газ, заключённый в цилиндрический объём с поршнем, движением которого изменяется объём газа (рис. 14.1).
|
| Рис. 14.1 |
Сила, создаваемая давлением газа  на поршень площади
на поршень площади  равна
равна  . Работа, совершаемая при перемещении поршня
. Работа, совершаемая при перемещении поршня  , равна
, равна  , где
, где  изменение объёма газа (рис. 14.1), то есть
изменение объёма газа (рис. 14.1), то есть
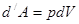
|
Теплота (количество теплоты) – количество энергии, получаемой или отдаваемой системой при теплообмене. Элементарное количество теплоты  не является в общем случае дифференциалом какой-либо функции параметров состояния. Передаваемое системе количество теплоты, как и работа, зависит от того, каким способом система переходит из начального состояния в конечное. (В отличие от внутренней энергии, для которой
не является в общем случае дифференциалом какой-либо функции параметров состояния. Передаваемое системе количество теплоты, как и работа, зависит от того, каким способом система переходит из начального состояния в конечное. (В отличие от внутренней энергии, для которой  , но
, но  , нельзя сказать, сколько работы содержит тело, “это функция” процесса – динамическая характеристика).
, нельзя сказать, сколько работы содержит тело, “это функция” процесса – динамическая характеристика).
1-ый закон (начало) термодинамики: количество теплоты, сообщённое системе, идёт на приращение внутренней энергии системы и на совершение системой работы над внешними телами.
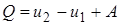
|
где  количество сообщённой телу теплоты;
количество сообщённой телу теплоты;
 и
и  начальное и конечное значения внутренней энергии;
начальное и конечное значения внутренней энергии;
 работа, совершённая системой над внешними телами.
работа, совершённая системой над внешними телами.
В дифференциальной форме 1-ое начало:

|
 сообщённое телу элементарное количество теплоты;
сообщённое телу элементарное количество теплоты;
 изменение внутренней энергии;
изменение внутренней энергии;
 совершённая телом работа (например, работа, совершённая при расширении газа).
совершённая телом работа (например, работа, совершённая при расширении газа).
11. Применение 1-го начала термодинамики к изопроцессам идеального газа
(Изопроцессы от  (греч.) – равный). Процессы, происходящие при каком-то постоянном параметре (
(греч.) – равный). Процессы, происходящие при каком-то постоянном параметре ( изотермический;
изотермический;  изобарический;
изобарический;  изохорический).
изохорический).
Теплоёмкостью  тела называется величина, равная отношению сообщённого телу количества теплоты
тела называется величина, равная отношению сообщённого телу количества теплоты  к соответствующему приращению температуры
к соответствующему приращению температуры  .
.

|
Размерность теплоёмкости тела 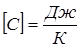 .
.
Аналогичные определения вводятся для 1 моля (молярная теплоёмкость
 ), и для единицы массы вещества
), и для единицы массы вещества  .
.
1. Рассмотрим нагревание газа при постоянном объёме. По первому закону термодинамики:
 , т.к.
, т.к.  , то
, то  .
.
 по определению, а для процесса с
по определению, а для процесса с  :
:
 , где
, где
 теплоёмкость газа при постоянном объёме.
теплоёмкость газа при постоянном объёме.
Тогда  и
и

|
2. Теплоёмкость газа при постоянном давлении:
 .
.
Для идеального газа для 1 моля (из уравнения Менделеева-Клапейрона).
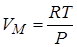 .
.
Продифференцируем это выражения по температуре Т, получим:
 , получим для 1 моля
, получим для 1 моля

|
Но выражение называется уравнением Майера. Оно показывает, что 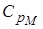 всегда больше
всегда больше 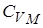 на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении по сравнению с процессом при постоянном объёме, требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.
на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении по сравнению с процессом при постоянном объёме, требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.
3. При адиабатическом процессе (процесс протекающий без теплообмена с внешней средой).
 ,
, 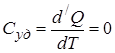 , т.е. теплоёмкость в адиабатическом процессе равна нулю.
, т.е. теплоёмкость в адиабатическом процессе равна нулю.
4. При изотермическом процессе  ,
,  , и, следовательно, теплоёмкость
, и, следовательно, теплоёмкость  .
.
Существуют процессы, при которых газ, расширяясь, совершает работу большую, чем полученная теплота, тогда его температура понижается, несмотря на приток теплоты. Теплоёмкость в этом случае отрицательна. В общем случае  .
.







