Энергия көздерінің басым көпшілігі үшін қысқа тұйықталу ережесі (кейде бос жүріс ережесі) рұқсат етілмейді. Энергия көзінің тоқтары мен кернеулері, қалыпты (номиналды) ережеге (тиімділігі және қызмет көрсету мерзімінің ұзақтығы жағынан алғанда оны пайдаланудағы ең жақсы (тиімді) шарттарға өндіруші кепілдік беретін режимге сәйкес) сәйкес келетін мәнде жоғарғы жағының шектелген белгілі бір аралықта өзгерулері мүмкін.
Бұл жағдайларда есептеуді оңайлату үшін жұмыстың m – n түзуінің аралығында сызықсыз ВАС – ны аппроксимациялауға мүмкіндік береді (1.5,б суретті қараңыз). Бұл түзудің орналасуы кернеу мен тоқтың өзгеруінің жұмыстық аралықтарымен (интервал) анықталады. Айта кету керек, көптеген энергия көздері (гальваникалық элементтер, аккумуляторлар) сызықты вольт – амперлік сипаттамаға ие.
2 түзуі келесі сызықтық теңдеумен сипатталады
бұл жерде Uбж – жүктемесі ажыратылған энергия көзінің қысқыштарындағы (зажим) кернеу.
- энергия көзінің ішкі кедергісі.
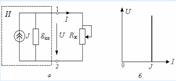
(1.1) теңдеуі ЭҚК көзінің тізбектелген орын басу сұлбасын құруға мүмкіндік береді (1.6, а суретті қараңыз). Бұл мүмкіндік Е символымен ЭҚК – нің идеал көзі деп аталатын элемент белгіленген. Бұл элементтің қысқыштарындағы кернеу энергия көзінің тоғына тәуелді емес, сәйкесінше, оған 1.6,б суретте көрсетілген ВАС сәйкес келеді. (1.1) негізінде мұндай энергия көзінің ішкі кедергісі нолге тен.
1.6 Сурет
Сонымен қатар тоқ көзінің орын басу сұлбасы орындалады. Бұны анықтау үшін (1.1) теңдеудің оң және сол жақтарын қатынасына бөлеміз. Нәтижесінде келесідегі теңдікті аламыз
немесе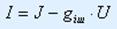 
(1.2)
мұндағы 
;
– қорек көзінің ішкі өткізгіштігі
(1.2) теңдеуі 1.7,а – суретіндегі орынбасу көзінің сұлбасына сәйкес келеді.
1.7 Сурет
Бұл сұлбадағы „ J ” символы идеалды тоқ көзі деп аталады. Тармақтағы бұл тоқ көзі 
тең және кернеу көздерінің қысқыштарына тәуелсіз, бұған сәйкесінше 1.7,б-суретіндегі ВАС-ны көруге болады. (1.2) теңдеуінің негізі мұндай көздерде 
, ал оның ішкі кедергісі 
.
Есептікте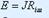 
шарты орындалу үшін орынбасу сұлбасының тізбектей және парраллельді қосылуынан эквивалентті пайда болады. Бірақ та энергетикалық жағынан олар әртүрлі болып келеді. Орынбасу сұлбасының тізбектей қосылуы үшін бос жүріс кезеңінде қуаты нөлге тең, ал параллельді қосылуы үшін болмайды.
Сонымен қатар практика жүзінде келісімді жұмыс кезеңі болады, яғни жүктеме көзінің максимальды пайдаланатын қуаты
(1.3)
Мұндай кезеңнің шарты
52. Кешенді кедергі және өткізгіштік, кешенді амплидуда үшін Ом заңы.
Кешенді кедергі тригонометриялық және көрсеткішті түрде былай жазылады Z = zcosφ+jzsinφ Z = zejφ = z< φ (6.8)
мұндағы z – Z кешенді санының модулі және тізбектің толық кедергісі, ал φ – Z кешен санының аргументі z = 
φ= 
arctg 
(6.6) негізінде тоқтың кешендік амплитудасы:
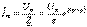
мұндағы ψ-φ тоқтың бастапқы фазасы. Осыған орай, тригонометриялық түрдегі ізделінген тоқ
i= Im(İm ejωt)=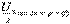 
6.5 Сурет
6.5 суретте кешендік жазықтық теңдеуінің (6.4) геометриялық түсіндіруі көрсетілген. 6.5,a - сурет тізбектің реактивті кедергісі индуктивтілік сипатқа (x>0) ие болғандағы және φ>0 жағдайға қатысты. 6.5б сурет тізбектің реактивті кедергісі сыйымдылық сипатқа (x>0) (φ<0) ие болғандағы жағдайға қатысты.
6.5 суретте келтірілген векторлық сызбада Ůr = ri - r кедергідегі кернеу (фаза бойынша I тоғына сәйкес келеді), ŮL=jωLI – L индуктивтегі кернеу
(I тоғын π/2 бұрышқа озады) және Uc=-j1/ωc*İ – C сыйымдылықтағы кернеу (I тоғынан π/2 бұрышқа қалады) Ur,UL,Uc векторларының геометриялық қосындысы тізбектегі U кернеуін береді.
