Периодты синусоидальды емес тоқтың тізбектеріндегі қуаты

Айнымалы периодикалық синусоидалды емес тоқтың орташа әсерлік мәні

Периодикалық тоқтың әсерлік мәні 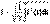(13.2) Периодты синусоидальды емес тоқты тригонометриялық қатарға саламыз 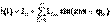және (13.2) кейіптемеге саламыз, түрлендіруден кейін мынаны аламыз. 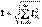(13.3)

Ұқсас кейіптемелер ЭҚК кернеулерінде де бар

Периодты синусоидальды емес тоқтың тізбектеріндегі қуаты

Кернеу мен тоқтың лездік мәндерін тригонометриялық қатар түрінде жазайық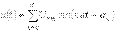

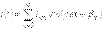
Онда,актив қуат үшін былай жазуға болады (13.4) Интегралдағаннан кейін аламыз (13.5) Осыдан, синусоидальды емес тоқтың актив қуаты актив қуаттардың бөлек гармоникалықтыларына тең болады Осыған ұқсас реактив қуат үшін жазуға болады: 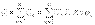Толық қуат 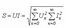Синусоидалы емес ток үшін

5.Электр тізбектерін түрлендіру. Бір сұлбаны келесімен ауыстру эквивалентті болып келеді, мұндай ауыстыруда тоқтар мен кернеулердің мәндері берілген аумақта өзгерісін келтіру міндет емес.1. Кедергілердің тізбектей қосылуын эквиваленттіге ауыстыру. Егер кедергілерді тізбектей қосқанда, бірдей тоқтар ағады. Тізбектің эквивалентті кедергісін анықтау үшін, яғни тізбектей қосқан кезде барлық кедергілердің қосындысына тең болады 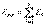(2.1) Тізбектің „ n ” кедергілерін тізбектей қосқан кезде, сондай кедергілерге бөлінеді де, осы кедергілерге тура пропорционалды болады. 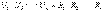Екі кедергіні тізбектей қосқан жағдайда 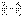, , 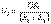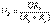мұндағы U – R₁R₂ кедергілерінен құралған, осы аумаққа әсер ететін жалпы кернеу. 2.Кедергілердің параллель қосуын эквивалленттіге ауыстыру. Егер кедергілер бір түйін бойынша қосылса, онда олар параллельді болып келеді. Тізбектің „ n ” параллельді қосылған кедергілердің эквиваленті келесідей кейіптемемен анықталады. 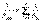НЕМЕСЕ (2.2) Екі кедергіні параллель қосқан жағдайда R_экв-ті кедергі келесідей анықталады

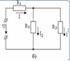2.1 Сурет Тізбектің „ n ” кедергілерін параллель қосқанда (2.1,а – сурет) әр тармақтың тоқтары кедергілерге кері пропорционалды немесе олардың өткізгіштіктеріне тура пропорционалды болып келеді.

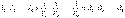I_S тоғы әрқайсысынан тармақталмаған тізбектің «I» тоғы арқылы есептеледі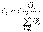

Екі тармақты параллель қосқан жағдайдағы (2.1,б – сурет), тоқтардың анықталуы

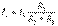
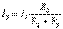НЕМЕСЕ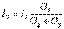

2.Кедергілердің аралас қосуын эквиваленттік ауыстыру. Тізбектердің тізбектей және параллель қосылуы аралас қосу болып келеді. Мысалы: R₁, R₂ және R₃ (2.1,б – сурет) кедергілері аралас қосылған. Олардың эквивалентті кедергісі 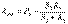= 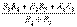ұшбұрышша қосылған кедергілерді (2.2,а – сурет) жұлдызшаға ауыстыру (2.2,б – сурет) және керісінше ауыстыру кезіндегі эквивалентті кедергілердің анықталуы

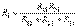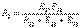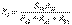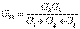, , (2.3) , , (2.4)

мұндағы G – сәйкес тармақтардың өткізгіштігі. (2.4) теңдеуін кедергілер арқылы келесідей жазуға болады

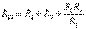, , (2.5)

2.2 Сурет

6. Өзара индуктивті байланысқан элементтерді тізбектей қосу. Индуктивті бaйланысқан элементтерді тізбектей қосу Кедергілері , индуктивтіктері 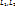бар екі индуктивті байланысқан катушка тізбектей қосылған. Қосылудың екі түрі бар: келісімді және қарсы.

Келісімді қосылу. Келісімді қосылған кезінде әрбір уақытта екі элементтердегі токтардың бағыттары аттас шықпаларға қарай бірдей, сондықтан әрбір элементпен ілініскен өздік индукцияның магнит ағындары және өзара индукцияның магнит ағындары бір-бірімен қосылады

,

Келісімді қосылу кезінде екі тізбектеп қосылған индуктивтік байланысқан элементтердің индуктивтігі

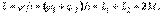
Бірінші және екінші катушкадағы қыстырғыштардағы кернеудің кешендік түрі

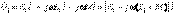
Тізбектің қысқыштарындағы кернеу

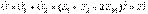
Қарсы қосылу. Қарсы қосылғанда тізбектің екі элементтерінде әрбір уақытта аттас шықпаларға токтардың бағыттары қарама-қарсы, сондықтан әрбір элементпен ілініскен өздік индукцияның және өзара индукцияның магнит ағындары бір-бірінен алынады.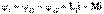

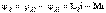
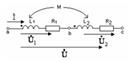
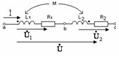Қарсы қосылу кезінде екі тізбектеп қосылған индуктивтік байланысқан элементтердің индуктивтігі

Бірінші және екінші катушкадағы қыстырғыштардағы кернеудің комплекстік түрі

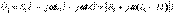
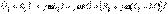Тізбектің қысқыштарындағы кернеу

келісімді қосылудың векторлық сызбасы (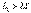 және кезінде).

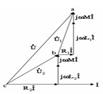
7. RLC элементтерін тізбектей қосу. Тізбектеп қосылған R,L және C элементерден құралған электр тізбектен 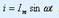синусойдалды тоқ өткенде: Тізбектеп қосылған кедергіде, индуктивтікте және сыйымдылықта синусойдалы тоқ кездегі кернеулер: тізбектің шықпаларында бөлек элементтердегі синусоидалды кернеулердің қосындысына тең синусоидалы кернеу құрылады 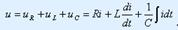Тізбектің шықпасындағыкернеу тең: 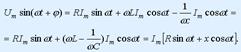Тізбектеп RLC қосылған тізбектің шықпаларындағы кернеу онда тізбектен ағып тұрған тоқ: Тізбектің түрі индуктивтік болса бұрыш болымды (x>0), ал сыйымдылық болса-теріс (x<0).

8. Кернеу резонансы. Жиіліктік сипаттамалары. Индуктивтілік пен сыйымдылығы бар тізбектің кірісіндегі кернеу мен токтардың фазалар айырмасы нолге тең болатын электр тізбегіндегі құбылысты резонанс дейді.Кернеу резонансы реактивті кіріс кедергі нолге тең болған кезде тізбектей жалғанған тербелмелі контурда пайда болады. 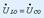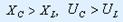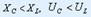Резонанс кезіндегі тізбектегі максималды ток: Контур кедергісі – минималды Резонанс режимінде Векторлық сызбалар:а) резонансқа дейін, болған кезде; в) резонанстан кейін, болганда: c) резонанс кезінде, болганда: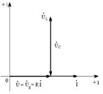

Контурдың жиілік сипаттамалары:

9. Тармақталған тізбекті есептеу үшін активті екіұштық әдісі. Эквивалентті генератор әдісі активті екіұштық теоремасына негізделген және электр тізбегінің қандай болмасын бір тармағында токты анықтауға мүмкіндік береді. Активті екіұштық теоремасының екі түрі: а) эквивалентті кернеу көзі туралы теорема;б) эквивалентті ток көзі туралы теорема. 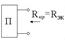Эквивалентті кернеу көзі: сызықты электр тізбегінің кез келген тармағындағы ток өзгермейді, егер берілген тармақ қосылған активті екіұштықты (екі шығарулары бар электр тізбегі), ашық тармақтағы кернеуге: пассивті екіұштықтың тармақтың ажыратылған жағынан кіріс кедергісіне: ЭҚК 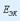бар эквиваленттік кернеу көзімен аустырса, 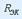ішкі кедергісіне тең.Ом заңы 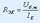бұл жерде 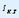- қысқа тұйықталу тогы. 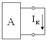R кедергісі бар тармақтың тоғы Ом заңымен анықталады: 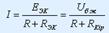немесе 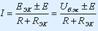, егер бөлінген тармақта ЭҚК Е көзі болса. «+» таңбасымен бағыты осы тармақтағы токтың бағытымен сәйкес келетін ЭҚК, «-» таңбасымен бағыты токтың бағытына қарама-қарсы болатын ЭҚК -тер жазылады.

10. Тоқ резонансы. Тоқ резонансының қисықтары және жиіліктік сипаттамасы. Индуктивтілік пен сыйымдылығы бар тізбектің кірісіндегі кернеу мен токтардың фазалар айырмасы нолге тең болатын электр тізбегіндегі құбылысты резонанс дейді.Ток резонансы реактивті кіріс өткізгіштігі нөлге тең болған параллель жалғанған тербелмелі контурда пайда болады. 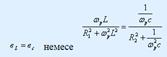Резонанс режиміндегі векторлық сызба: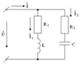

Резонанстық жиілік: 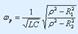контурдың жиіліктік сипаттамасы: резонанстың қисығы: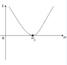

11. Кирхгофтың I, II заңдары (тұрақты тоқ тізбегі үшін). Кирхгофтың заңдарын жазу үшін тармақтағы тоқтың бағытын оң бағытта бағыттау керек. Кирхгофтың бірінші заңы – электр тізбегінің түйініндегі электр тоғының алгебралық қосындысы нөлге тең

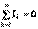. (3.1) Түйінен шығатын тоқ шартты түрде оң, ал түйінге бағытталған тоқ теріс деп қабылданады (немесе керісінше). Кирхгофтың екінші заңы – тұйық контурдағы ЭҚК-нің алгебралық қосындысы ондағы кернеудің түсуінің алгебралық қосындысына тең 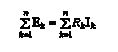(3.2) Контурдың айналу бағыты өз еркінше таңдалады. Теңдіктің сол жағын жазған кезде ЭҚК-нің бағыты таңдап алынған айналу бағытына сәйкес келсе – оң деп қабылданады, ол қарсы бағытталса – теріс деп қабылданады. Теңдіктің оң жағын жазған кезде контурдағы таңдап алынған оң бағытталған тоқтың бағыты айналу бағытына сәйкес келсе, тармақтағы кернеудің түсуін оң таңбамен жазамыз, ал тоқтың оң бағыты айналу бағытына қарсы болса, кернеудің түсуін теріс таңбамен жазамыз.Тізбек 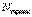тармақтан, 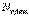түйіннен және 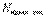идеал тоқ көзінен тұрсын. Кирхгоф заңдарын қолданамыз. 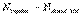тең болатын белгісіз тоқтардың санын орнатамыз. Әр тармаққа тоқтың оң бағытымен орнатылады. Кирхгофтың бірінші және екінші заңдары бойынша құрастырылатын теңдеулердің жалпы саны () белгісіз тоқтың санына тең. Кирхгофтың бірінші заңына байланысты құрастыратын теңдеулер саны (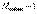)-ге тең. Кирхгофтың екінші заңы бойынша құрастырылатын өзара тәуелсіз теңдеулер саны: 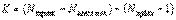. (3.3)

12)Периодикалық синусоидалды емес электр тізбегінің қуаттары. Кернеу мен тоқтың лездік мәндерін тригонометриялық қатар түрінде жазайық 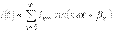, .Онда, актив қуат үшін былай жазуға болады

(13.4) Интегралдағаннан кейін аламыз

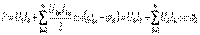13.5)Осыдан, синусоидальды емес тоқтың актив қуаты актив қуаттардың бөлек гармоникалықтыларына тең болады

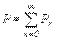.Осыған ұқсас реактив қуат үшін жазуға болады: 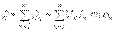.Толық қуат 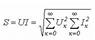.Синусоидалы емес ток үшін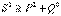

13)RL тізбегінің кіріс сипаттамасы (АЖС және ФЖС). Кіріс сипаттама деп тәуелділігі аңғарылады. 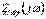кешенді шама болғандықтан, оны төмендегідей түрде көрсетуге болады: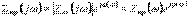

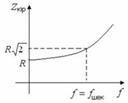
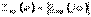- кіріс сипаттамасының модулі амплитуда-жиіліктік сипаттама деп аталады (АЖС);

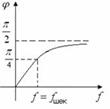
ф(w)- кіріс сипаттаманың аргументі тізбектің фаза-жиіліктік сипаттамасы деп аталады (ФЖС).

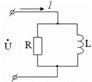RL тізбегі үшін 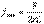сонда, 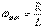немесе . ; :

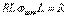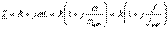14)Периодикалық синусоидалды емес ЭҚК, кернеу және токтың әсерлік мәндері. Периодтық функция 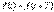мұндағы Т – период, Дирихленің шартын қанағаттандыратын, Фурьенің тригонометриялық қатарына жіктеуге болады. 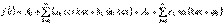мұндағы - тұрақты құраушы немесе нөлдік гармоника. 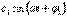-бірінші (негізгі) гармоника, 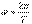бұрыштық жиілігімен өзгереді.Периодикалық тоқтың әсерлік мәні

Периодты синусоидальды емес тоқты тригонометриялық қатарға саламыз 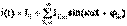осыдан,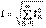

Ұқсас кейіптемелер ЭҚК кернеулерінде де бар

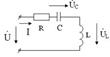
15)R,L,C тізбектерін параллель қосу Егер параллель қосылған r, L, C (6.6 - сурет) элементтерінен тұратын

u = U_msinωt синусоидалды кернеу тіркелген болса, онда осы тізбекпен өткен синусоидалды тоқ мынаған тең болады i=i_r+i_L+i_C 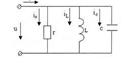6.6 Суре т 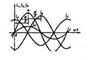6.7 Сурет

r кедергідегі i_r тоғы фаза бойынша U кернеуімен сәйкес келеді, L индуктивтегі i_L тоғы қалса, С сыйымдылықтағы i_С тоғы π/2 бұрышқа озады.Сондықтан тізбектегі жалпы тоқ мынаған тең

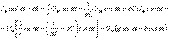(6.10) b = b_L-b_c=(1/ωC)- ωC тізбектің реактивті өткізгіштігі деп аталады да, таңбаға байланысты (b>0) индуктивті сипаттама немесе сыйымдылық сипаттама (b<0) болады. g=1/r – активті өткізгіш деп аталады.Кирхгофтың бірінші заңы бойынша İ=gŮ+Ů 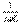+jωCŮ=İ_r+İ_L+İ_C (6.11)мұндағы I_r=gŮ – кедергідегі тоқ (фаза бойынша U кернеумен сәйкес келеді). İ=- Ů - индуктивтіліктегі тоқ İ=jωCŮ - сыйымдылықтағы тоқ Кешенді өткізгіш мынаған тең Y =g-j(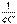 -ωC)=g-jb. (6.12) Кешенді түрдегі Ом заңының теңдеуі İ= Y Ů (6.13) Тригонометриялық және көрсеткіш түрдегі кешендік өткізгіш келесідей болады Y = у cos φ-jsin φ; Y=ye^{-j φ} мұндағы у – кешенді санының модулі Y - тізбектің толық өткізгіштігі φ – Y кешенді санының аргументі у =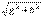 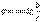(6.14) Кешенді тоқ мынаған тең i = yUe^J(y-j) Бұл синусоидалды тоққа i = I_m(İ_me^jω) =yU_msin(ωt + ψ - φ) сәйкес келеді 6.8 суретте кешенді жазықтық теңдеуiнің геометриялық түсіндірілуі көрсетілген. 6.8,a - сурет тізбектің реактивті өткізгіштігі индуктивтілік сипатта (b>0) болғандағы жағдайға ие болып, сонымен қатар тоқ фаза бойынша кернеуден қалады (φ>0). 6.8, б - сурет тізбектің реактивті өткізгіштігі сыйымдылық сипатқа (b<0) ие болып, тоқ фаза бойынша кернеуден озады (φ < 0). 6.8 Сурет

 

16)Контулық токтар әдісі (тұрақты тоқ үшін). Бұл әдіс тармақтан өтетін тізбектегі кез келген тармақтағы тоқты контурлық тоқтардың алгебралық қосындысы түрінде жазуға болатындығына негізделген. Осы әдісті қолданған кезде контурлық тоқтарды таңдайды және белгілейді (тізбектің кез келген тармағы арқылы кемінде бір таңдап алынған контурлық тоқ өту керек). Контурлық тоқтардың жалпы саны -ге тең. Контурлық тоқтардың -ның әр біреуі бір тоқ көзінен өтуі ұсынылады. Осы контурлық тоқтарды сәйкес тоқ көздерімен сәйкес келеді деп санауға болады және олар әдетте есептің шартында беріледі. Бұлар үшін теңдеулер құрастырылмайды, бірақ басқа контурларға теңдеулер құраған кезде ескеріледі. Қалған контурлық тоқтар тоқ көзі жоқ, тармақтардан өтетіндерін таңдайды. Кирхгофтың екінші заңына байланысты соңғы контурлық тоқтарды анықтаған кезде К теңдеулері

· R11I11 + R12Ι22 + … +R1kIkk+ … +JnRn = Е11,

· R21I11 + R22Ι22 + … +R2kIkk+ … +JnRn = Е22, (3.4)

· Rk1I11 + Rk2Ι22 + … +RkkIkk+ … +JnRn = Еkk

түрінде жазылады. Мұндағы Rnn- n контурының өзінің кедергісі (n контурына кіретін барлық тармақтардың кедергілерінің қосындысы); Rn1- Rn n және L контурларының жалпы кедергісі, Rnl = Rln. n және L үшін жалпы тармақтағы контурлық тоқтардың бағыты сәйкес келсе, онда Rn1 оң, ал егер керісінше болса Rn1 теріс болады; Еnn –n контурын құрайтын тармақтарға қосылған ЭҚК-нің алгебралық қосындысы; Rn-тармақтағы n контуры мен тоқ көзі бар контурдың жалпы кедергісі

 

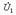17)RC тізбегінің беріліс сипаттамасы (АЖС және ФЖС) Кернеудің беріліс функциясының кешенді еселеуіші қатынасымен анықталады.мұндағы - шығыс кернеуі - кіріс кернеуі. Беріліс еселеуіштерінің арақатынасы (совокупность) әртүрлі жиілікте кешенді беріліс функциясы деп аталады және келесідей белгіленеді 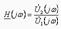немесе 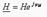мұндағы Н – модулі (беріліс функциясының АЖС) – аргумент (беріліс функциясының ФЖС). RC және Rн (9.10 сурет) тізбектері үшін қарапайым мысал беріліс функциясының кернеуін қарастырайық.

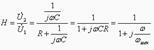
(9.5) (9.6) 9.5 және 9.6 теңдеулері бойынша сәйкес беріліс функциясынан АЖС-ын және ФЖС-ын құрайық.

18)RL және RC элементтерін тізбектей қосу.

XL=wL –индуктивті кедергі. W=R+jXL – кіріс кедергісі (кешенді); I=U/z cosf=R/z; f=arccosR/z; sinf=XL/z; f=arcsinXL/z; tgf=XL/R; f=arctgXL/R; UR=iR (лездік);UR=IR (кешендік);

UL=L(di/dt); UL=IjXL; U=UR+UL=iR+L(di/dt) (лездік мәні);U=UR+UL=IR+IjXL=I(R+jXL)=IZ (кешендік)

z=R-jXc; Xc=1/wC;w=2pif; Xc=-pi/2

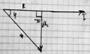cosf=R/z=arccosR/z; sinf=Xc/z=arcsinXc/z; tgf=Xc/R=arctgXc/R; I=U/z=U/(R-jXc); U=UR+Uc=IR+I(-jXc)=I(R-jXc)=Iz;

U=UR+Uc=iR+/C 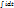(лездік мәні)

 

18)Түйіндік потенциалдар әдісі (тұрақты тоқ тізбегі үшін). 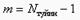санына дейін құрастырылатын теңдеулер санын қысқартады. Бұл әдістің негізі алдымен теңдеулер жүйесін шешу арқылы сұлбадағы барлық түйіндердің потенциалын анықтау, ал түйіндерді біріктіретін тармақтың тоғын Ом заңы арқылы табады. Түйіндік потенциалдар әдісімен теңдеулер құрастырылған кезде кез келген түйіндегі потенциалды нөлге теңестіреді (оны базистік деп атайды). Қалған () түйіндердегі потенциалдарды анықтау үшін келесі теңдеулер жүйесі құрастырылады.

мұндағы Gss –S түйініне қосылған тармақтың өтімділігінің алгебралық қосындысы; Gsq – S түйінімен q түйінін қосатын тармақтардың алгебралық қосындысы; - S түйініне кіретін тармақтағы ЭҚК-нің көбейтіндісінің алгебралық қосындысы; оң таңбамен S түйінінің бағытына сәйкес әсер ететін ЭҚК, кері таңбамен - S түйінінен шығатын ЭҚК алынады. - S түйініне қосылған тоқ көзінің алгебралық қосындысы; S түйінге бағытталған тоқ, оң таңбамен, ал S түйінінен бағытталған тоқ теріс таңбамен алынады. Теңдеулер саны контурлық тоқтар әдісімен құралған теңдеулер санынан кем болған жағдайда, түйіндік потенциалдар әдісін қолдану ұсынылады. Егер сұлбада кейбір түйіндер идеал тоқ көзінің ЭҚК қосылған болса m теңдеулер саны, түйіндік потенциалды әдісімен табылған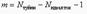

мұндағы - идеал тоқ көзіне қосылған ЭҚК-дегі тармақ саны. Тармаққа қатысты идеал тоқ көзінің ЭҚК-дегі кез келген бір түйін нөлге теңестіріледі, сол кезде қалған потенциалдар болады. Егер ЭҚК бағытымен бағытталса, оң болады, қарсы болса – теріс таңбамен алынады. Тармақтардағы тоқтар Ом заңы бойынша анықталады.

 

20)Екі түйіндік потенциалдар әдісі (тұрақты тоқ тізбегі үшін). Екі түйіні бар сұлбалар үшін (мысалы «а» және «в» түйіндері), түйіндегі кернеу Uab мына кейіптемемен анықталады Uab = 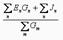мұндағы ∑ΕnGn – тармақтағы ЭҚК-нің алгебралық қосындысының көбейтіндісі (егер ЭҚК «а» түйінге бағытталса оң, егер «а» түйіннен «в» бағытталса теріс) және осы тармақтардың өздік өткізгіштігінің қөбейтіндісі. Jn – тоқ көзіндегі тоқтар (түйінге бағытталған болса оң, егер «а» түйіннен «в» бағытталса теріс). 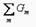- «а» және «в» түйіндерін қосатын барлық тармақтардың өткізгіштігінің қосындысы.

 

21)Индуктивті байланысқан элементтерді параллель қосу. Тізбектің екі катушкасы кедергілері, индуктивтіктері параллель қосылған және де олардың аттас шықпалары бір түйінге қосылған (10.4 - сурет).

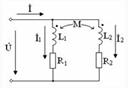10.4 Сурет.Тізбек үшін Кирхгоф заңын жазамыз (10.4 - сурет) 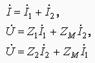(10.16) тмұндағы , , 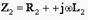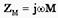.(10.16) теңдігін шешкенде, мынаны аламыз 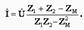(10.17) Тізбектің кіріс кедергісі (10.18) Түйінге аттас емес шықпалармен қосылып тұрғанда қарайық 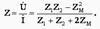(10.19)

22)RL тізбегінің беріліс сипаттамасы (АЖС және ФЖС). Кешенді беріліс функциясы (КБФ) 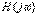кешенді тізбек реакция шамасының кешенді кіріс шамасына арақатынасымен анықталады. Кіріс шамасының типіне және тізбек реакциясына байланысты КБФ келесі түрге бөлінеді: 1. Кернеу бойынша кешенді беріліс функциясы (6.1) 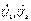- Кернеудің кешенді әсерлік мәнінің кірісіндегі әсері және шығысындағы кернеу реакциясы. 2. Ток бойынша кешенді беріліс функциясы 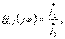(6.2) 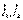- Токтардың кешенді әсерлік мәнінің әсерлік мәнінің әсері және ток реакциясы. 3. Кешенді беріліс кедергісі 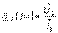(6.3)4. Кешенді беріліс өткізгіштігі 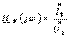(6.4) 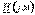кешенді шамасы мынаған тең

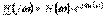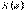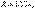
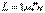мұндағы - АЖС КБФ; - ФЖС КБФ. 6.3.мысал тізбегі үшін (6.5-сурет) АЖС және ФЖС кешенді беріліс функциясының кернеуі бойынша графигін салу. Бұрыштық жиіліктің өзгерісінің шегі 0-ден 2⁴с^-1 дейін. 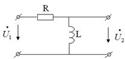6.5 Сурет Кернеу бойынша кешенді беріліс функциясын сипаттаймыз

АЖС және ФЖС көрсетеміз: , .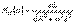

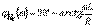23) Периодикалық синусоидалды емес электр тізбегі жалпылама анықтамалар. Тәжірибеде ЭҚК, кернеу, тоқ азды – көпті болса да синусоидальды емес болады. Ол нақты генераторлар қамтамасыз етпейтінімен байланысты, нақты айтқанда, қисық кернеудің синусоидальды түрі және тізбекте сызықсыз элементтің болуы тоқтың бұрмалауына синусоидальды ЭҚК көзі болса да жаңа шарт туғызады. Радиотехникада, есептеу техникасында периодикалық синусоидальды емес импульстардың генераторы қолданылады.Жалпы жағдайда синусоидальды емес өлшемдердің өзгеру сипаттамасы периодикалық, жартылай периодикалық және периодикалық емес болуы мүмкін. Осы дәрісте синусоидальды емес периодикалық ЭҚК, кернеуі, тоғы бар тізбектерді ғана қарастырамыз.