1. Проведем первичную обработку данных.
Ymin=0,014; Ymax=0,05.
Все остальные значения наблюдаемой величины находятся в промежутке [Ymin;Ymax]. Разобьем отрезок на интервалы равной длины.
Найдем длину частичного интервала.
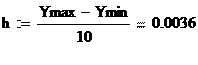
|
За начало первого интервала a0 возьмем значение случайно величины, равное Ymin-h/2
Для каждого из полученных интервалов найдем правый конец по формуле аi=аi-1+h, i=1,….11.
Будем считать полученные интервалы закрытыми слева.
Далее подсчитаем число значений случайно величины X, попавших в каждый из полученных интервалов (используем функцию ЧАСТОТА).
Вычислим относительные частоты W(i)=n(i)/n
Также для составления дискретного ряда распределения случайной величины найдем середины полученных интервалов x(i).
Результаты вычислений представим в таблице (5).
Таблица 5.
| a | интервалы | n(i) | w(i) | y(i) | |
| a1 | 0,0122 | 0,0158 | 0,04 | 0,014 | |
| a2 | 0,0158 | 0,0194 | 0,06 | 0,0176 | |
| a3 | 0,0194 | 0,023 | 0,16 | 0,0212 | |
| a4 | 0,023 | 0,0266 | 0,19 | 0,0248 | |
| a5 | 0,0266 | 0,0302 | 0,25 | 0,0284 | |
| a6 | 0,0302 | 0,0338 | 0,09 | 0,032 | |
| a7 | 0,0338 | 0,0374 | 0,11 | 0,0356 | |
| a8 | 0,0374 | 0,041 | 0,05 | 0,0392 | |
| a9 | 0,041 | 0,0446 | 0,02 | 0,0428 | |
| a10 | 0,0446 | 0,0482 | 0,01 | 0,0464 | |
| a11 | 0,0482 | 0,0518 | 0,02 | 0,05 | |
| Сумма |
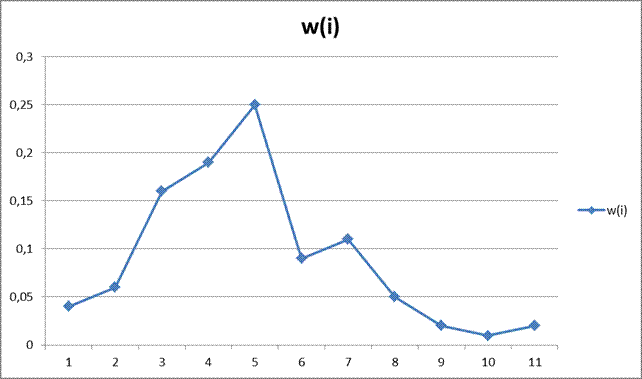
2. Построим гистограмму и полигон относительных частот:

3. Вычислим числовые характеристики выборки.
Для удобства вычислений числовых характеристик выборки составим таблицу (6).
| n(i) | y(i) | y(i)*n(i) | (x(i)-x(вх))^2*n(i) | (y(i)-y(вх))^3*n(i) | (x(i)-x(вх))^4*n(i) |
| 0,014 | 0,056 | 0,000772395 | -1,07332E-05 | 1,49149E-07 | |
| 0,0176 | 0,1056 | 0,000636046 | -6,54873E-06 | 6,74257E-08 | |
| 0,0212 | 0,3392 | 0,000717383 | -4,80359E-06 | 3,21649E-08 | |
| 0,0248 | 0,4712 | 0,000182119 | -5,63841E-07 | 1,74565E-09 | |
| 0,0284 | 0,71 | 6,3504E-06 | 3,2006E-09 | 1,6131E-12 | |
| 0,032 | 0,288 | 0,000151585 | 6,22106E-07 | 2,55312E-09 | |
| 0,0356 | 0,3916 | 0,000652868 | 5,02969E-06 | 3,87488E-08 | |
| 0,0392 | 0,196 | 0,000638902 | 7,22215E-06 | 8,16392E-08 | |
| 0,0428 | 0,0856 | 0,000444258 | 6,62123E-06 | 9,86828E-08 | |
| 0,0464 | 0,0464 | 0,000342398 | 6,33573E-06 | 1,17236E-07 | |
| 0,05 | 0,1 | 0,000977174 | 2,15994E-05 | 4,77434E-07 | |
| 2,7896 | 0,005521478 | 2,47842E-05 | 1,06678E-06 |
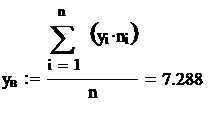
|

|

|
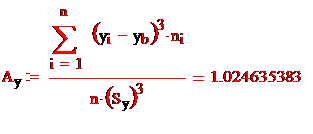
|
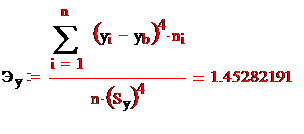
|
4. Установим тип распределения случайной величины.
В нашем примере вид полигона позволяет сделать предположение о том, что распределение наблюдаемой величины следует нормальному закону. Проверим эту статическую гипотезу.
Сформулируем нулевую H0 и конкурирующую H1 гипотезы. согласно условию задачи.
H0: распределение случайной величины Х следует по нормальному закону.
H1: случайная величина Х не подчиняется нормальному закону распределения.
Проверим гипотезу H0, пользуясь критерием согласия Пирсона.
Предполагая, что гипотеза H0 верна, найдем теоретические вероятности попадания случайной величины X в интервал по формуле:
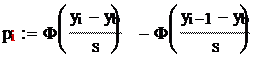
|
Где Ф(х)- функция Лапласа.
Затем найдем теоретические частоты np и наблюдаемое значение статистики критерия Пирсона.

|
Для вычисления функции Лапласа используем функцию НОРМСТРАСП.
Также найдем χ^2(кр) по заданному уровню значимости и числу степеней свободы.
Составим таблицу (7) расчетов.
Таблица 7.
| Интервалы | n(i) | p(i) | np(i) | (n(i)-np(i))^2\np(i) | |
| 0,0122 | 0,0158 | 0,034475 | 3,447462 | 0,08855722 | |
| 0,0158 | 0,0194 | 0,074684 | 7,468396 | 0,288708137 | |
| 0,0194 | 0,023 | 0,128532 | 12,85324 | 0,77039784 | |
| 0,023 | 0,0266 | 0,175744 | 17,57437 | 0,115646176 | |
| 0,0266 | 0,0302 | 0,190917 | 19,09166 | 1,828469265 | |
| 0,0302 | 0,0338 | 0,164781 | 16,47812 | 3,393731025 | |
| 0,0338 | 0,0374 | 0,112997 | 11,29966 | 0,007946703 | |
| 0,0374 | 0,041 | 0,06156 | 6,156006 | 0,217080808 | |
| 0,041 | 0,0518 | 0,038304 | 3,830364 | 0,357158756 | |
| Сумма | 0,981993 | 98,19928 | 7,067695931 |
χ^2(набл)=7,067695931
χ^2(кр)= 12,59158724
χ^2(набл)< χ^2(кр)
Отсюда следует, при данном уровне значимости выдвинутая гипотеза H0 согласуется с экспериментальными данными.
Cоставим корреляционную таблицу, записав вместо интервалов соответствующие им середины.
Таблица 8.
| 2,8 | 4,12 | 5,44 | 6,76 | 8,08 | 9,4 | 10,72 | 12,04 | 13,36 | 14,68 | ny | |||
| 0,014 | 0,434 | ||||||||||||
| 0,0176 | 0,64416 | ||||||||||||
| 0,0212 | 2,041136 | ||||||||||||
| 0,0248 | 3,578144 | ||||||||||||
| 0,0284 | 5,136992 | ||||||||||||
| 0,032 | 1,98912 | ||||||||||||
| 0,0356 | 2,647216 | ||||||||||||
| 0,0392 | 2,35984 | ||||||||||||
| 0,0428 | 0,748144 | ||||||||||||
| 0,0464 | 0,191168 | ||||||||||||
| 0,05 | 1,072 | ||||||||||||
| nx | 20,84192 |
По данным корреляционной таблицы, вычислим корреляционный момент.

|
Kxy=0,005113152
rв=Kxy/Sx*Sy=0,266151155
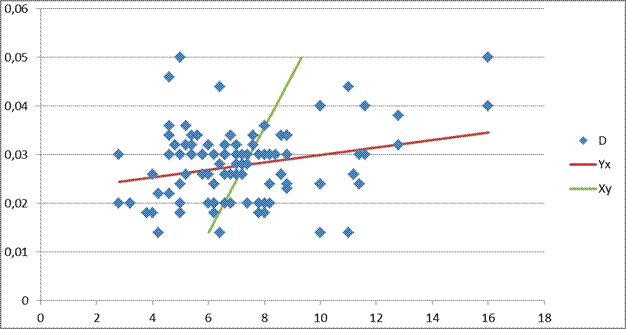
Найдем выборочное уравнение регрессии Y и X (используем MathCad)
yx=yв+ rв*Sy/Sx*(x-xв)= 0.00077265952940781091771*x+0.022264857349675874032
xy=xв+ rв*Sx/Sy*(y-yв)= 91.678720848916679466*y+4.7305304031986203096
Проверка:
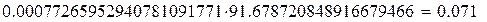
|

|
Для подтверждения гипотезы о существовании линейной зависимости между исследуемыми случайными величинами X u Y построим корреляционное поле. Для этого изобразим результаты измерений в виде точек в декартовой системе координат. Также построим на этом рисунке полученные прямые, определяемые полученными уравнениями линий регрессий.