Задача 1. На двох шнурах однакової довжини, яка дорівнює 0,8 м, підвішені дві свинцевих кулі масами 0,5 і 1 кг. Кулі стикаються між собою. Кулю меншої маси відвели убік так, що шнур відхилився на кут a = 60°, і відпустили. На яку висоту піднімуться обидві кулі після зіткнення? Удар вважати центральним і непружним. Визначити енергію, яка витрачається на деформацію куль при ударі.
Розв’язування. Так як удар куль непружний, то після удару кулі будуть рухатися з загальною швидкістю v. Закон збереження імпульсу при цьому ударі має вигляд:
(1)
Тут v1 і v2 – швидкості кульок до удару. Швидкість великої кулі до удару дорівнює нулю. Швидкість меншої кулі знайдемо використовуючи закон збереження енергії. При відхиленні меншої кулі на кут a вона здобуває потенціальну енергію, яка потім переходить у кінетичну:
.
Із рисунка видно, що
,
тому:
. (2)
З рівнянь (1) і (2) знаходимо швидкість куль після удару:
. (3)
Кінетична енергія, яку мають кулі після удару, переходить у потенціальну:
(4)
де h – висота, на яку піднімуться кулі після зіткнення.
З формули (4) знаходимо
.
Враховуючи (3), отримаємо:
, 
.
При непружньому ударі куль частина енергії витрачається на їхню деформацію. Енергія деформації знаходиться як різниця кінетичних енергій до і після удару:
.
Використовуючи рівняння (2) і (3), одержуємо:
, 
.
Задача 2. Молот масою 70 кг падає з висоти 5 м і вдаряє по залізному виробу, що лежить на ковадлі. Маса ковадлі разом з виробом 1330 кг. Вважаючи удар абсолютно непружним, визначити енергію, що витрачається на деформацію виробу. Систему вважати замкнутою.
Розв’язування. За умовою задачі система молот-виріб-ковадло вважається замкнутою, а удар непружний. За законом збереження енергії можна вважати, що енергія, яка витрачена на деформацію виробу, дорівнює різниці значень механічної енергії системи до і після удару. Вважаємо, що під час удару змінюється тільки кінетична енергія тіл, тобто незначним переміщенням тіл по вертикалі під час удару зневажаємо. Тоді для енергії деформації виробу маємо:
(1)
де v – швидкість молота наприкінці падіння з висоти h, v’ – швидкість тіл системи після непружнього удару.
Швидкість молота наприкінці падіння визначається без врахування опору повітря і тертя за формулою
. (2)
Загальну швидкість тіл системи після непружнього удару знайдемо за допомогою закону збереження імпульсу:
(3)
Для розглянутої системи закон збереження імпульсу має вигляд:
,
відкіля знаходимо:
(4)
Підставивши у формулу (1) вираження (2) і (4), одержимо:
.
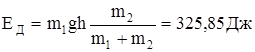Задача 3. Тіло масою 1 кг під дією постійної сили рухається прямолінійно. Залежність шляху, який пройшло тіло, від часу задана рівнянням 
Визначити роботу сили за 10 с з початку її дії і залежність кінетичної енергії від часу.
Розв’язування. Робота, яку виконує сила, виражається наступним чином:
(1)
Сила, що діє на тіло, за другим законом Ньютона дорівнює
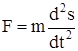. (2)
Миттєве значення прискорення знайдемо як другу похідну від шляху за часом:
(3),
(4)
Тоді
. (5)
З вираження (3) визначимо ds:
(6)
Підставивши (5) і (6) у рівняння (1), одержимо
.
По цій формулі визначимо роботу, яку виконує сила за 10 с з початку її дії:
.
Кінетичну енергію знайдемо за формулою:
. (7)
Підставляючи (3) у (7), маємо:
