1) Рассмотрим силы давления жидкости на полностью погруженное в неё тело ABCD произвольной формы.
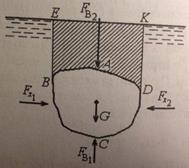Горизонтальные составляющие силы 
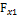и 
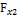, действующие на вертикальные проекции криволинейных поверхностей, равны по величине, но имеют разные знаки, т е взаимно уравновешиваются. Также будут равны и взаимно противоположные силы давления на поверхность тела в перпендикулярной к чертежу плоскости.
|
Вертикальные силы давления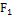 
и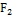 
на криволинейные поверхности ABC и ADC определяются по величине, как силы тяжести тел давления, опирающихся на эти поверхности:
, 
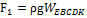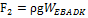, равнодействующая: 
.
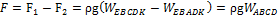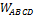– водоизмещение – объем вытесненной жидкости.
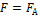– сила Архимеда (выталкивающая сила) приложена к центру водоизмещения.
Закон Архимеда: на погруженное в жидкость тело (или часть) действует сила гидростатического давления направленная вертикально вверх и равная силе тяжести жидкости, вытесненной погружением.
2) На законе Архимеда основана теория плавания тел. Всякое погруженное в жидкость тело находится под действием 2х сил: силы тяжести тела G и равнодействующей силы давления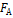 
.
Условия плавания тел: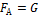 
– тело находится в равновесии, 
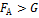– тело всплывает или плавает, 
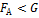– тело тонет.
Для плавающего на поверхности однородного тела с плотностью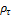 
и объемом 
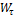будем иметь условие равновесия: 
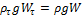или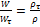 
, 
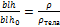, тогда 
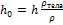– осадка, глубина погружения (h – высота тела).
3) Ватерлиния – линия пересечения свободной поверхности жидкости с боковой поверхностью плавающего тела.
Плоскость плавания – плоскость внутри тела, ограниченная ватерлинией.
вертикальная ось плавания – вертикальная ось О-О’, проходящая через центр водоизмещения.
Эксцентриситет – расстояние м/д центром тяжести С и центром водоизмещения D.
Остойчивость – способность плавающих тел восстанавливать нарушенное при крене равновесие.
Метоцентр – точка М пересечения линии действия выталкивающей силы 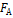, прходящей через точку D’ и оси плавания.
При наклоне плавающего тела его центр тяжести не изменит своего положения, а центр водоизмещения D переместится в положение D’.
Взаимное положение метацентра и центра тяжести определяет остойчивость плавающего тела
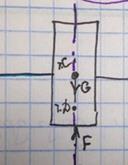
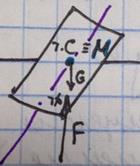
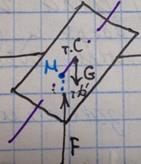
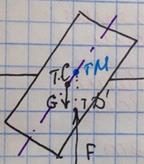
а б в г
а – нормальное положение.
б – неостойчивое безразличное равновесие, т к метацентр совпадает с центром тяжести. (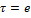
, 
)
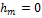в – неостойчивое равновесие, т к метацентр ниже центра тяжести. (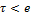
, 
)
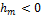г – остойчивое равновесие, т к метацентр выше центра тяжести. (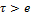
, 
)
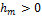τ =MD – метацентрический радиус, e=CD – эксцентриситет, MD=MD’ при φ<15°,
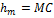- метацентрическая высота,
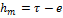, τ=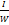 
, где I – момент инерции площади плавания относительно продольной оси.
Характеристика остойчивост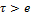и: или .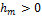
