Перевод из двоичной системы в 8- и 16-ричную

Перевод в десятичную систему счисления

Если число в b -ричной системе счисления равно

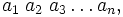
то для перевода в десятичную систему вычисляем такую сумму:

или, в более наглядном виде:

либо, наконец, в виде схемы Горнера:

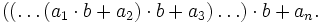
Например:

101100₂ =

= 1 · 2⁵ + 0 · 2⁴ + 1 · 2³ + 1 · 2² + 0 · 2¹ + 0 · 1 =

= 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 =

= 32 + 8 + 4 + 0 = 44₁₀

Перевод из десятичной системы счисления

Целая часть

1. Последовательно делить целую часть десятичного числа на основание, пока десятичное число не станет равно нулю.
2. Полученные при делении остатки являются цифрами нужного числа. Число в новой системе записывают, начиная с последнего остатка.

Дробная часть

1. Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
2. Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.

Пример

44₁₀ переведём в двоичную систему:

44 делим на 2. частное 22, остаток 0

22 делим на 2. частное 11, остаток 0

11 делим на 2. частное 5, остаток 1

5 делим на 2. частное 2, остаток 1

2 делим на 2. частное 1, остаток 0

1 делим на 2. частное 0, остаток 1

Частное равно нулю, деление закончено. Теперь записав все остатки снизу вверх получим число 101100₂

Перевод из двоичной в восьмеричную и шестнадцатеричную системы

Для этого типа операций существует упрощённый алгоритм.

Для восьмеричной — разбиваем переводимое число на количество цифр, равное степени 2 (2 возводится в ту степень, которая требуется, чтобы получить основание системы, в которую требуется перевести (2³=8), в данном случае 3, то есть триад). Преобразуем триады по таблице триад:

000 0 100 4

001 1 101 5

010 2 110 6

011 3 111 7

Для шестнадцатеричной — разбиваем переводимое число на количество цифр, равное степени 2 (2 возводится в ту степень, которая требуется, чтобы получить основание системы, в которую требуется перевести (2⁴=16), в данном случае 4, то есть тетрад). Преобразуем тетрады по таблице тетрад:

0000 0 0100 4 1000 8 1100 C

0001 1 0101 5 1001 9 1101 D

0010 2 0110 6 1010 A 1110 E

0011 3 0111 7 1011 B 1111 F

Пример:

преобразуем 101100₂

восьмеричная — 101 100 → 54₈

шестнадцатеричная — 0010 1100 → 2C₁₆

Перевод из восьмеричной и шестнадцатеричной систем в двоичную

Для этого типа операций существует упрощённый алгоритм-перевёртыш.

Для восьмеричной — преобразуем по таблице в триплеты

0 000 4 100

1 001 5 101

2 010 6 110

3 011 7 111

Для шестнадцатеричной — преобразуем по таблице в квартеты

0 0000 4 0100 8 1000 C 1100

1 0001 5 0101 9 1001 D 1101

2 0010 6 0110 A 1010 E 1110

3 0011 7 0111 B 1011 F 1111

Пример:

преобразуем

54₈ → 101 100

2C₁₆ → 0010 1100

Перевод из двоичной системы в 8- и 16-ричную

Перевод дробной части из двоичной системы счисления в системы счисления с основаниями 8 и 16 осуществляется точно также, как и для целых частей числа, за тем лишь исключением, что разбивка на октавы и тетрады идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа. Например, рассмотренное выше число 1100,011₂ будет выглядеть как 14,3₈ или C,6₁₆.