ax2 + bx + c = а(х – х1)(х – х2)= а(х - 0,5b:a)2 – 0,25D:a.
Дискримінант D = b2 – 4ac. Два корені: х1 = (‒ b ‒ (b2 ‒ 4ac)0,5)/(2a), х2 = (‒ b + (b2 ‒ 4ac)0,5)/(2a). Координати вершини квадратичної параболи: хв = - 0,5b:a; ув = - -0,5b:a.
xy + x + y + а = (х + 1)(y + 1) + а - 1.
xy + x + y + 1 = (х + 1)(y + 1)
aху + bх + cу + d = (x + c:a)(ау + b) + d – (cb:a).
Якщо b2 ‒ 4ac – невід’ємний, то ax2 + byх + cy2 = а(х ‒ k1y) (х ‒ k2y),
де k1, k2 ‒ корені квадратного рівняння ak2 + bk + c = 0.
Можливість виділення з многочлена лінійних множників пов’язана з наявністю у цього многочлена дійсних коренів.
Властивість 1. Довільний многочлен від однієї змінної з цілими коефіцієнтами приймає тільки непарні значення при будь-яких цілих значеннях змінних, якщо у нього одночасно виконуються дві умови:
1) многочлен має вільний член, що виражений непарним числом;
2) сума усіх коефіцієнтів многочлена, без вільного члена, парна.
Властивість 2. Довільний многочлен від однієї змінної з цілими коефіцієнтами приймає тільки непарні значення при будь-яких цілих значеннях змінних, якщо у нього кількість непарних коефіцієнтів многочлена разом із вільним членом, непарна.
Властивість 3. Довільний многочлен від однієї змінної з цілими коефіцієнтами немає цілих коренів, якщо у нього одночасно виконуються умови:
1) многочлен має вільний член, що виражений непарним числом;
2) сума усіх коефіцієнтів многочлена, окрім вільного члена, парна.
Властивість 4. Довільний многочлен від однієї змінної з цілими коефіцієнтами немає натуральних коренів, якщо у нього одночасно виконуються умови:
1) многочлен має вільний член;
1) усі коефіцієнти многочлена разом з вільним членом, одного знаку.
Властивість 5. Довільний многочлен від однієї змінної з цілими коефіцієнтами має корінь 1, якщо у нього сума усіх коефіцієнтів разом із вільним членом дорівнює нулю.
Властивість 6. Довільний многочлен від однієї змінної з цілими коефіцієнтами одного знаку має корінь х = -1, якщо у нього сума усіх коефіцієнтів, що стоять при парних степенях змінної, включаючи вільний член, рівна сумі усіх коефіцієнтів, що стоять при непарних степенях змінної.
Властивість 7. Довільний многочлен від однієї змінної з дійсними коефіцієнтами має хоча б один дійсний корінь, якщо у нього коефіцієнти при найбільшому степені змінної і вільний член – це два числа, що мають різні знаки.
Властивість 8. Довільний многочлен парного степеня(окрім нульового степеня) від однієї змінної з дійсними коефіцієнтами має хоча б два дійсних корені, якщо у нього коефіцієнти при найбільшому степені змінної і вільний член – це два числа, що мають різні знаки, при цьому знаки дійсних коренів різні.
Властивість 9. Довільний многочлен f(x) парного степеня(окрім нульового степеня) від однієї змінної з дійсними коефіцієнтами має хоча б один дійсний корінь, якщо знайдеться таке натуральне n таке, що добуток f(n)f(0)< = 0.
Властивість 10. Якщодовільний многочлен від однієї змінної з цілими коефіцієнтами не приймає парні значення при будь-яких цілих значеннях змінних, то у нього немає цілих коренів.
Властивість 11. Якщодовільний многочлен від однієї змінної з цілими коефіцієнтами приймає значення тільки одного знаку(або тільки додатні, або тільки від’ємні) при будь-яких цілих значеннях змінних, то у нього немає цілих коренів.
Властивість 12. Довільний многочлен f(x) будь-якого степеня(окрім нульового степеня) від однієї змінної з цілими коефіцієнтами має парним значенням наступне число f(а) + f(-а) та парне значення: f(а):а + f(-а):(-а)=0, де а – вільний член многочлена. Тобто, корнем многочлена
f(х):х + f(-х):(-х)=0 є вільний член f(x).
Звертаємо вашу увагу, що рівняння не має розв'язків у цілих числах, якщо для довільних цілих значень змінної в лівій і правій частинах рівняння одержуються цілі числа, для яких виконується хоча б одна з таких умов:
1)Ліва і права частини під час ділення на деяке ціле число дають різні остачі.
Наприклад, у рівнянні n3-n = 3m2+1 для довільних цілих чисел ліва частина рівняння, тобто вираз
n(n - 1)(n + 1),
ділиться на 3, а права частина під час ділення на 3 дає в остачі 1.
2)Остання цифра числа в лівій частині інша, ніж остання цифра числа в правій частині.
Наприклад, у рівнянні
х2+х -1 = 32у+1
для довільних натуральних х та у числа, які одержуються в лівій частині, закінчуються цифрами 1, 5 і 9, а числа, які одержуються в правій частині, закінчуються цифрами 3 і 7.
3) Одна з частин рівняння є точним квадратом (кубом), але друга частина такою не є.
Наприклад, у рівнянні
4m = 3∙k + 2
ліва частина для довільного натурального m є точним квадратом, тоді як права частина ні для якого натурального k не може бути точним квадратом (точний квадрат під час ділення на 3 дає в остачі або 0, або 1).
Довідник. Формули скороченого множення
для трьох змінних
Однією з таких якісних характеристик може бути парність.
Наводимо ще такі властивості парності чисел:
2∙n + 2∙k + … + 2∙f + 2∙q = 2∙(n + k + … + f + q) = 2∙m
СУМА БУДЬ-ЯКОЇ КІЛЬКОСТІ ПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
2∙n – 2∙k – … – 2∙f – 2∙q = 2∙(n – k – … – f – q) = 2∙m
РІЗНИЦЯ БУДЬ-ЯКОЇ КІЛЬКОСТІ ПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
(2∙n -1)+ (2∙k-1)+ … + (2∙f-1) + (2∙q-1) = 2∙(n + k + … + f + q)- 2s = 2∙(m-s)
СУМА ПАРНОЇ КІЛЬКОСТІ НЕПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
(2∙n -1)+ (2∙k-1)+ … + (2∙f-1) + (2∙q-1) = 2∙(n + k + … + f + q)- 2s -1 = 2∙(m-s) - 1
СУМА НЕПАРНОЇ КІЛЬКОСТІ НЕПАРНИХ ЧИСЕЛ ЗАВЖДИ ПАРНА.
Таким чином, парність результату суми та різниці натуральних чисел не залежить від розстановки плюсів і мінусів, а залежить тільки від кількості непарних чисел в початковому наборі. Зрозуміло, що сума будь-якої кількості парних чисел є завжди парним числом.
Добутки двох множників, що містять три змінні
(a + b + c)2 = (a + b + c)(a + b - c)= a2 + b2 + c2 + 2аb + 2bc +2ac;
(a + b + c)(a + b - c)= (a + b)2 – c2 = a 2 + 2b a + b2 – c2;
(a - b + c)(a + b - c)= a2 - b2 + 2b c – c 2 = a2 -(c - b)2;
(a - b - c)(a - b - c)= a2 + b2 + c 2 + 2b c – 2ab -2a c = a2 -(c - b)2;
(a - b - c)(a + b - c)= a2 - b2 + c2 -2ac =(a - c)2 -b2;
Деякі факти про розклад цілих многочленів на множники
Нехай а1, а2, а2, …, аn – попарно різні цілі числа. Тоді:
А) многочлен (х - а1) (х - а2)(х - а2) … (х - аn) - 1 – незвідний, тобто не розкладається на многочлени меншого степеня;
Б) многочлен (х - а1)(х - а2)(х - а2) … (х - аn) + 1 – незвідний, тобто не розкладається на многочлени меншого степеня, окрім наступних випадків:
(х – а)(х – а - 2) + 1 = (х – а - 1)2;
(х - а) (х – а - 1) (х – а - 2)(х - а - 3) + 1 = ((х – а - 1(х – а - 2) – 1)2;
В) многочлен (х - а1)2(х - а2)2(х - а2)2 … (х - аn)2 + 1 – незвідний, тобто не розкладається на многочлени меншого степеня;
Г) якщо р – просте число, то многочлен хр – х – 1 – незвідний, тобто не розкладається на многочлени меншого степеня;
Д) якщо р – просте число, а – натуральне число, що не ділиться на р, то многочлен хр – х – а – незвідний, тобто не розкладається на многочлени меншого степеня;
Є) будь-який многочлен з цілими коефіцієнтами можна записати як суму двох незвідних многочленів.
Тотожності.
1 =  m =
m = 
m2 =  m2 =
m2 = 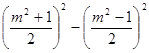
mn = 
Добутки трьох множників, що містять три змінні
Завдання 1.
Чому не існує трійки цілих чисел (a; b; c), яка задовольняє такі рівняння:
А) (a+ b)(a + c)(b + c)= 1; Б) (a - b)(a - c)(b - c)= 1;
В) (a + b)(a - c)(b - c)= 1; В) (a + b)(a - c)(b - c)= 1;
Г) (a + b)(a + c)(b - c)= 1?
Відповідь. (a+ b)(a + c)(b + c) - цей вираз завжди парне число, якщо усі змінні – це цілі числа.
Завдання 2.
Чи існують трійки цілих чисел (a; b; c), які задовольняє
А) (a - b)(a - c)(b - c)= 2; А) (a - b)(a - c)(b - c)= 0;
Відповідь. А) Існують такі трійки чисел: (n; n-1; n-2) (n; n-1; n+1) (n; n+2; n+1), де n - ціле числа. Б) Існують такі трійки чисел: (n; n; k) (k; n; n) (n; k; n), де n, k - цілi числа.
(a - b)(a - c)(b - c)= a2b -аb2 + ac2- a2c + b2c - bc2 - цей вираз завжди парне число, якщо усі змінні – це цілі числа.
(a + b)(a + c)(b + c)= a2b +аb2 + ac2+ a2c + b2c + bc2 +2abc; - цей вираз завжди парне число, якщо усі змінні – це цілі числа.
(a - b)(a + c)(b - c)= a2b -аb2 - ac2- a2c - b2c + bc2 +2abc; - цей вираз завжди парне число, якщо усі змінні – це цілі числа.
(a - b)(a + c)(b + c)= a2b - аb2 + ac2+ a2c - b2c - bc2; - цей вираз завжди парне число, якщо усі змінні – це цілі числа.
Завдання 3.
Знайти трійку чисел (a; b; c) яка задовольняє (a - b)(a - c)(b - c)= -1
Сума трьох квадратів із трьох змінних
(a + b + c)2 +(a - b - c)2 +(a + b - c)2 = 3a2 + 3b2+ 3c2+ 2а2b + 2аb2 -2a2c
цей вираз буде непарним числом, якщо тільки одна змінна є непарне число або усі три змінні є непарними числами.
(a + b + c)(a - b - c)(a + b - c) = a3 - b3 +c3 + а2b - аb2 -a2c - c2a - b2c + c2b+2abc;
а3 + b3 + c3 - 3abc = (a+b+c)(a2 + b2 +c2 –аb–bc–ac);
(a + b - c)2 = a2 + b2 + c2 + 2аb - 2bc -2ac;
(a - b - c)2 = a2 + b2 + c2 - 2аb + 2bc -2ac;
(a + b + c)2 = a2 + b2 + c2 + 2аb + 2bc +2ac;
(a + b + c)3 = a3 + b3+ c3+ 3а2b + 3аb2 +3a2c +3ac2+3b2c+3bc2+6abc;
(a - b - c)3 = a3 - b3- c3- 3а2b + 3аb2 -3a2c +3ac2-3b2c-3bc2+6abc;
(a + b - c)3 = a3 + b3- c3+ 3а2b + 3аb2 -3a2c +3ac2-3b2c+3bc2-6abc;
(a + b + c)(a + b - c)(a - b + c)(a + b + c) = (a2 – (b - c)2) (a + b + c)2
(a + b + c)(a + b - c)(a - b + c)(b + c- а) = 2a2c2 +2b2c2 +2b2a2 – a4– b4– c4
Парні та непарні значення квадратного тричлена
Усі три незалежних цілих коефіцієнти a, b, c можуть приймати одне із двох значень: парне або непарне. Всього існує вісім різних випадків запису квадратного тричлена з цілими коефіцієнтами за критерієм парності:
Всього існує шістнадцять різних випадків цілих значень квадратного тричлена з цілими коефіцієнтами:
| ax2 + bx + c = f(x), якщо х = 2m | |||
| ax2 + | bx + | c | = f(2m) |
| 2n(2m)2 + | (2p – 1)(2m) + | 2k | =2q |
| 2n(2m)2 + | (2p – 1)(2m) + | (2k – 1) | =2q - 1 |
| 2n(2m)2 + | 2p(2m) + | (2k – 1) | =2q - 1 |
| 2n(2m)2 + | 2p(2m) + | 2k | =2q |
| (2n – 1) (2m)2 + | (2p – 1)(2m) + | (2k – 1) | =2q - 1 |
| (2n – 1) (2m)2+ | (2p – 1)(2m) + | 2k | =2q |
| (2n – 1) (2m)2 + | 2p(2m) + | 2k | =2q |
| (2n – 1) (2m)2 + | 2p(2m) + | (2k – 1) | =2q - 1 |
| a | x2+ | b | x+ | c | =f(x) |
| 2n | x2+ | (2k – 1) | x+ | 2q | =f(x) |
| 2n | x2+ | (2k – 1) | x+ | (2q – 1) | =f(x) |
| 2n | x2+ | 2k | x+ | (2q – 1) | =f(x) |
| 2n | x2+ | 2k | x+ | 2q | =f(x) |
| (2n – 1) | x2+ | (2k – 1) | x+ | (2q – 1) | =f(x) |
| (2n – 1) | x2+ | (2k – 1) | x+ | 2q | =f(x) |
| (2n – 1) | x2+ | 2k | x+ | 2q | =f(x) |
| (2n – 1) | x2+ | 2k | x+ | (2q – 1) | =f(x) |
Теорема. Довільний многочлен стандартного вигляду з цілими коефіцієнтами при парних значеннях змінної приймає таку ж парність, яку має вільний член.
Теорема. Довільний многочлен стандартного вигляду з цілими коефіцієнтами серед своїх цілих коренів немає парних коренів, якщо вільний член виражений непарним числом.
Доведення. Таблиця дає повну картину значень квадратного тричлена при парних значеннях х:
| ax2 + bx + c = f(x), якщо х = 2m | |||
| ax2 + | bx + | c | = f(2m) |
| 2n(2m)2 + | (2p – 1)(2m) + | 2k | =2q |
| 2n(2m)2 + | 2p(2m) + | 2k | =2q |
| (2n – 1) (2m)2+ | (2p – 1)(2m) + | 2k | =2q |
| (2n – 1) (2m)2 + | 2p(2m) + | 2k | =2q |
| 2n(2m)2 + | (2p – 1)(2m) + | (2k – 1) | =2q - 1 |
| 2n(2m)2 + | 2p(2m) + | (2k – 1) | =2q - 1 |
| (2n – 1) (2m)2 + | (2p – 1)(2m) + | (2k – 1) | =2q - 1 |
| (2n – 1) (2m)2 + | 2p(2m) + | (2k – 1) | =2q - 1 |
Теорема. Довільний многочлен стандартного вигляду з цілими коефіцієнтами серед своїх цілих коренів немає парних коренів, якщо вільний член виражений непарним числом.
Доведення. Якщо вільний член виражений непарним числом, то значення квадратного тричлена f(2m) = 2q - 1, і ніколи не буде дорівнювати нулю, бо нуль – це парне число.
Оглянемо таблицю значень квадратного тричлена при непарних значеннях зиінної:
| ax2 + bx + c = f(x), якщо х = 2m – 1 | |||
| ax2 + | bx + | c | = f(x) |
| 2n(2m – 1)2 + | (2p – 1)(2m – 1) + | 2k | =2q - 1 |
| 2n(2m – 1)2 + | (2p – 1)(2m – 1) + | (2k – 1) | =2q |
| 2n(2m – 1)2 + | 2p(2m – 1) + | (2k – 1) | =2q - 1 |
| 2n(2m – 1)2 + | 2p(2m – 1) + | 2k | =2q |
| (2n – 1) (2m – 1)2 + | (2p – 1)(2m – 1) + | (2k – 1) | =2q - 1 |
| (2n – 1) (2m – 1)2 + | (2p – 1)(2m – 1) + | 2k | =2q |
| (2n – 1) (2m – 1)2 + | 2p(2m – 1) + | 2k | =2q - 1 |
| (2n – 1) (2m – 1)2 + | 2p(2m – 1) + | (2k – 1) | =2q |
Або
| ax2 + bx + c = f(x), якщо х = 2m – 1 | |||
| ax2 + | bx + | c | = f(x) |
| 2n(2m – 1)2 + | 2p(2m – 1) + | 2k | =2q |
| (2n – 1) (2m – 1)2 + | (2p – 1)(2m – 1) + | 2k | =2q |
| 2n(2m – 1)2 + | (2p – 1)(2m – 1) + | (2k – 1) | =2q |
| (2n – 1) (2m – 1)2 + | 2p(2m – 1) + | (2k – 1) | =2q |
| 2n(2m – 1)2 + | 2p(2m – 1) + | (2k – 1) | =2q - 1 |
| (2n – 1) (2m – 1)2 + | (2p – 1)(2m – 1) + | (2k – 1) | =2q - 1 |
| (2n – 1) (2m – 1)2 + | 2p(2m – 1) + | 2k | =2q - 1 |
| 2n(2m – 1)2 + | (2p – 1)(2m – 1) + | 2k | =2q - 1 |
Теорема. Якщо існують цілі корені зведеного квадратного тричлена, то вони мають однакову парність(або обидва корені непарні, або обидва корені парні), якщо b – парне число, і два корені мають різну п арність коренів(тільки один із коренів парний, а другий корінь – непарний), якщо b – непарне число.
Доведення. Випадок 1. Два цілі корені існують і обидва парні, тобто 2k i 2n. Тоді згідно теореми Вієта у зведеного квадратного тричлена стандартного вигляду лінійний коефіцієнт дорівнює протилежній сумі цих двох парних коренів, а отже має бути записаний як 2m.
Випадок 2. Два цілі корені існують і обидва непарні, тобто 2k-1 i 2n-1. Тоді згідно теореми Вієта у зведеного квадратного тричлена стандартного вигляду лінійний коефіцієнт дорівнює протилежній сумі цих двох непарних коренів, а отже має бути записаний як 2m.
Випадок 3. Два цілі корені існують і один непарний, а інший парний тобто 2k-1 i 2n. Тоді згідно теореми Вієта у зведеного квадратного тричлена стандартного вигляду лінійний коефіцієнт дорівнює протилежній сумі цих непарного і парного коренів, а отже має бути записаний як 2m-1.
Теорема. Якщо існують цілі корені зведеного квадратного тричлена, і вони обидва парні, тоді вільний член цього многочлена кратний 4.
Доведення. Два цілі корені існують і обидва парні, тобто 2k i 2n. Тоді згідно теореми Вієта у зведеного квадратного тричлена стандартного вигляду вільний член повинен бути рівний добутку цим двом парним кореням, а отже має бути записаний як 4m.
Теорема. Якщо у зведеного квадратного тричлена стандартного вигляду (тобто а = 1) із цілим вільним членом та лінійним коефіцієнтом такими, що обидва непарні, то квадратний тричлен не має цілих коренів.
Доведення. Від супротивного. Припустимо, що цілі корені існують. Тоді у зведеного квадратного тричлена стандартного вигляду вільний член повинен бути кратний цілим кореням, а так як він виражений непарним числом, то його дільники це тільки непарні. А сума двох непарних дільників парна, і ця парність рівна парності лінійного коефіцієнта згідно теореми Вієта, що порушує задану умову непарності лінійного коефіцієнта.
Теорема. Якщо у квадратного тричлена стандартного вигляду із цілими коефіцієнтами а та b і с = 2k-1 такими, що обидва а та b однакової парності, то квадратний тричлен не має цілих коренів.
Доведення. Усі значення тричлена при цілих значеннях змінної – непарні!, Тому тричлен ніколи не дорівнюватиме нулю при цілих значеннях змінної.
Дивиться сайт для підготовки до ЗНО
http://zno0432.blogspot.com/2015/05/blog-post.html






