Прямые показатели качества – время переходного процесса (время регулирования) tпп и перерегулирование σ определяется по реакции замкнутой системы на единичное ступенчатое воздействие, вид которого показан на рис 1
Время регулирования tпп определяется по моменту вхождения кривой в пятипроцентную зону от установившегося значения.
Период перерегулирования находится из выражения:
σ=(ymax-yy)/yy*100%

Рис. 1 Реакции системы на единичное ступенчатое воздействие
Косвенные показатели качества, определяемые по расположению корней характеристического уравнения замкнутой системы на комплексной плоскости.
В число основных оценок входит степень устойчивости (быстродействия) η и колебательность μ (рис. 2).

Система устойчива, когда все корни находятся в левой полуплоскости.

Рис. 2 Комплексная плоскость
Косвенные показатели качества устойчивости замкнутой системы, определяемые по ее ЛЧХ в разомкнутом состоянии: запас устойчивости ΔL по амплитуде, запас устойчивости Δφ по фазе и частота среза ωср (рис.3)

Рис.3 ЛЧХ и ЛФЧХ разомкнутой системы
Косвенные показатели качества, определяемые по АЧХ замкнутой системы. Оценками качества являются показатель колебательности М (рис.4)

Рис. 4 ЛЧХ замкнутой системы
Показатель колебательности находят из выражения Аmax(ω)=20 LgM. При этом для того чтобы система была устойчива необходимо чтобы M=(1,3÷1,7)
23 Понятие существенной и несущественной нелинейности
Автоматическая система управления является нелинейной, если хотя бы один ее элемент описывается нелинейным уравнением.
Практически все реальные системы управления содержат один или несколько нелинейных элементов. Нелинейной характеристикой часто обладает и объект управления. Так, например, все электрические машины имеют нелинейную и неоднозначную зависьимость магнитного потока от тока возбуждения. Индуктивности обмоток машины также зависят от токов.
Некоторые нелинейные элементы вводят в систему преднамеренно, чтобы улучшить качество управления. Такими нелинейностями являются, например, релейные управляющие устройства, обеспечивающие высокое быстродействие процесса управления. Применяются также нелинейные корректирующие устройства
Различают два вида нелинейных элементов: существенно нелинейные и несущественно нелинейные. Нелинейность считается несущественной, если ее замена линейным элементом не изменяет принципиальных особенностей системы и процессы в линеаризованной системе качественно не отличаются от процессов в реальной системе. Если такая замена невозможна, и процессы в линеаризованной и реальной системах сильно отличаются, то нелинейность является существенной Главная особенность существенно нелинейных систем заключается в том, что они не подчиняются принципу наложения, а форма и показатели переходного процесса зависят от величины и формы внешнего воздействия.
Другой важной особенностью динамики существенно нелинейных систем является зависимость условий устойчивости от величины внешнего воздействия. В связи с этим для нелинейных систем применяют понятия "устойчивость в малом", "устойчивость в большом", "устойчивость в целом".
Система устойчива в малом, если она устойчива только при малых начальных отклонениях. Система устойчива в большом, если она устойчива при больших начальных отклонениях. Система устойчива в целом, если она устойчива при любых отклонениях.
24 Постановка задачи синтеза корректирующих устройств
В настоящее время существует несколько постановок задач проектирования (синтеза) электромеханических моделей автоматизированных систем, заключающихся в выборе структурной схемы, параметров, способа технической реализации разработанного модуля из условия выполнения ряда требований к проектируемой автоматизированной системе и обеспечению ее характеристик. Одним из способов описания требований к проектируемому ЭММ может служить задание показателей качества работы ЭММ как допустимое значение статической, динамической и средней квадратической ошибок. При этом должны быть известны характеристики управляющих и возмущающих воздействий. Детерминированные воздействия должны быть заданы как функции времени или их производные. Случайные сигналы и помехи должны быть определены их корреляционными функциями или спектральными плотностями.
Если управляющий сигнал описывается медленно меняющейся функцией времени, а сигнал возмущения отсутствует, то используют первый способ проектирования САУ ЭММ, выполняя задачу синтеза в следующем порядке:
1) для объекта управления (ОУ) по техническим условиям выбирают регулирующий орган с силовым приводом, усилительно-преобразовательное устройство (УПУ) и датчики. Объединяя силовые устройства и устройства информационного канала линиями связи, формируют неизменяемую часть ЭММ;
2) по статическим и динамическим характеристикам выбранных устройств составляют передаточные функции отдельных элементов, формируют структурную схему, определяют места включения корректирующих устройств (последовательное, параллельное и последовательно-параллельное);
3) по заданным требованиям на запас устойчивости по фазе, амплитуде соответственно показателям качества и точности строят желаемые логарифмические амплитудные (ЛАЧХЖ) и фазовые частотные характеристики (ЛФЧХ) разомкнутой системы ЭММ;
4) по построенным желаемым (ЛАЧХЖ) и логарифмическим характеристикам неизменяемой (нескорректированной) части (ЛАЧХНС) определяют коэффициент усиления дополнительно вводимых промежуточных усилителей, а также тип и параметры корректирующих устройств.
Второй способ используют, когда на синтезируемую систему действует возмущение, описываемое в форме прямого преобразования Лапласа. В этом случае задачу синтеза выполняют для наиболее полного подавления возмущения при минимальном значении ошибки в системе.
Третий способ применяют, когда в системе действуют управляющий и возмущающий сигналы одновременно. В этом случае синтезируемая система должна наиболее точно отрабатывать управляющий сигнал и подавлять влияние возмущения.
25 Построение ЖЛАЧХ приближенными методами
Правила построения ЛАЧХ одноконтурной системы:
1. Определяют сопрягающие частоты звеньев  ,
,  и т.д. и отмечают их вдоль оси частот.
и т.д. и отмечают их вдоль оси частот.
2. Проводят низкочастотную асимптоту ЛАЧХ – L(w), которая представляет собой при w<w1=wmin прямую с наклоном 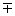 20n дБ/дек (-n - порядок астатизма системы, определяемый числом интегрирующих звеньев; +n - число дифференцирующих звеньев в контуре; n=0 – для статических систем). Эта прямая линия или ее продолжение проходит через точку, имеющую ординату, равную 20lgK дБ, на частоте w=1, где К – передаточный коэффициент разомкнутой системы.
20n дБ/дек (-n - порядок астатизма системы, определяемый числом интегрирующих звеньев; +n - число дифференцирующих звеньев в контуре; n=0 – для статических систем). Эта прямая линия или ее продолжение проходит через точку, имеющую ординату, равную 20lgK дБ, на частоте w=1, где К – передаточный коэффициент разомкнутой системы.
3. После каждой из сопрягающих частот wi наклон характеристики L(w) изменяют по сравнению с тем наклоном, который эта характеристика имела до сопрягающей частоты wi в соответствии с видом звена, которому принадлежит эта частота. Наклон изменяют: на -20дБ/дек, если сопрягающая частота принадлежит апериодическому звену; на -40дБ/дек – колебательному звену или инерционному звену второго порядка; на +20дБ/дек – дифференцирующему или форсирующему звену первого порядка; на +40дБ/дек – дифференцирующему (форсирующему) звену второго порядка.
4. Уточняют вид L(w) при помощи таблиц или кривых поправок.
Следует отметить, что высокочастотная асимптота ЛАЧХ, т.е. её часть при частотах, больших наивысшей сопрягающей частоты, должна иметь наклон -20(n-m)дБ/дек, где n – порядок знаменателя, m – порядок числителя передаточной функции W(s).
ЛФЧХ одноконтурной системы получаются в результате сложения ординат фазовых характеристик типовых звеньев, входящих в ее состав.
При построении графиков ЛАЧХ и ЛФЧХ по оси абсцисс откладывают значения частоты w в логарифмическом масштабе (1декада = 50мм), по оси ординат откладывают значения 20lgA(w) в равномерном масштабе (20мм = 20дБ).
ЛАЧХ разомкнутой САУ может быть разбита на три характерных участка (рис3. 19).

Рис 3.19. Области частотЛАЧХ(w1- первая сопрягающая частота; wс- частота среза; wв- наибольшая сопрягающая частота)
Область низких частот – участок ЛАЧХ, лежащий в области частот, меньших первой сопрягающей частоты. Вид ЛАЧХ в этой области определяет порядок астатизма и статическую точность системы. Для статических системЛАЧХ в этой области – горизонтальная прямая, отстоящая от оси частот на величину 20lgКраз.
Область средних частот. Определяет в основном запас устойчивости и качество САУ. В этом интервале находится частота среза системы wс, характеризующая время переходного процесса при достаточных запасах устойчивости. Область средних частот заканчивается частотой wв.
Область высоких частот (wв ¸ ¥). Этот участок может быть назван интервалом малых параметров. Он содержит сопрягающие частоты, пренебрежение которыми не оказывает существенного влияния на вид ЛАЧХ в интервале средних частот.
26 Построение ЖЛАЧХ
- На частоте
 фиксируется точка с амплитудой 20 lg
фиксируется точка с амплитудой 20 lg 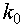 .
. - Отмечаются частоты сопряжения
 .
. - До первой частоты сопряжения строится НЧ асимптота с наклоном (-20) r дБ/дек, если передаточная функция объекта содержит интегрирующие звенья, а r - число таких звеньев. Наклон будет равен +20 l дБ/дек, если
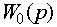 содержит дифференцирующие звенья, l - число таких звеньев. НЧ асимптота или ее продолжение должна пересекать точку 20 lg
содержит дифференцирующие звенья, l - число таких звеньев. НЧ асимптота или ее продолжение должна пересекать точку 20 lg 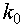 .
. - На частоте сопряжения происходит излом асимптотической ЛАЧХ объекта. Он будет равен -20 r дБ/дек, если соответствующая постоянная времени находится в знаменателе передаточной функции объекта, r - число таких звеньев. Наклон будет равен +20 l дБ/дек, если постоянная времени находится в числителе передаточной функции, l - число таких звеньев. Асимптота проводится до следующей частоты сопряжения, где также происходит ее излом.
Пример 6.3.
Построить асимптотическую ЛАЧХ объекта, передаточная функция которого имеет вид:
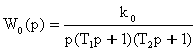 ,
,
где коэффициент передачи k0=10, а постоянные времени T1=10c,T2=1c.
 Риc.6.10. Асимптотическая ЛАЧХ объекта
Риc.6.10. Асимптотическая ЛАЧХ объекта
| При построении ЛАЧХ воспользуемся предложенной процедурой. С этой целью определим характерные точки:
20 lg k0 = 20 дБ;
lg  1 = lg 1/T 1 = lg 0,1 = -1 дек;
lg 1 = lg 1/T 1 = lg 0,1 = -1 дек;
lg  2 = lg 1/T 2 = lg 1 = 0,
которые откладываются на осях координат (рис.6.10.). 2 = lg 1/T 2 = lg 1 = 0,
которые откладываются на осях координат (рис.6.10.).
|
Если передаточная функция объекта представлена выражением общего вида,
 ,
,
то следует перейти к частотной характеристике  Для построения ЛАЧХ объекта используем выражение
Для построения ЛАЧХ объекта используем выражение  что позволяет определить
что позволяет определить 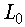 (
(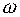 ) в виде
) в виде

то есть ЛАЧХ объекта находится как разность ЛАЧХ его числителя и знаменателя.
28Принцип абсолютной компенсации
29. Связь переходного процесса с ВЧХ
Вещественная частотная характеристика замкнутой системы Re=P(ω) позволяет приближенно оценить качество переходной характеристики и в случае необходимости построить переходный процесс. Поэтому данную характеристику часто используют при инженерных расчетах. Примерный вид вещественной частотной характеристики замкнутой системы по заданному воздействию показан на рис.5. 3.

Рис.5.3. Вещественная частотная характеристика
Интервал частот, в котором Р(ω) положительна, называется интервалом положительности ωп. Значение частоты ωсч (существенная частота), после которой кривая Р(ω) не выходит за пределы участка ± 0.1Р(0), определяет примерно границу пропускания частот исследуемой системы, если она статическая. На частоты, лежащие за пределами полосы пропускания ωсч, система практически не реагирует.
Качество переходной характеристики можно приближенно оценить по следующим признакам Р(ω).
Признак 1. Установившееся значение переходной характеристики (конечное значение) 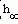 = h(
= h( ) равно начальному значению вещественной частотной характеристики Р(0).
) равно начальному значению вещественной частотной характеристики Р(0).
Признак 2. Начальное значение переходной характеристики h0=h(0) равно конечному значению вещественной частотной характеристики Р( ).
).
Признак 3. При наличии у положительной вещественной частотной характеристики максимума Рmax перерегулирование δ переходного процесса приближенно равно

Признак 4. Не возрастающая положительная вещественная частотная характеристика с отрицательной и убывающей по абсолютной величине производной соответствует монотонному переходному процессу.
Признак 5. Если увеличить (уменьшить) масштаб Р(ω) вдоль оси абсцисс в n раз, то масштаб кривой переходного процесса вдоль оси времени уменьшится (увеличится) в тоже число раз.
Признак 6. Если изменить масштаб Р(ω) вдоль оси ординат в n раз, то и масштаб кривой переходного процесса вдоль той же оси времени изменится во столько же раз.
Признак 7. Если вещественная частотная характеристика положительна при частотах ω<ωr, то время регулирования в общем случае заведомо больше  .
.
Признак 8. При положительной невозрастающей вещественной частотной характеристике перерегулирование переходного процесса не может превышать 18 %.
Признак 9. Острый пик вещественной характеристики при угловой частоте ωр свидетельствует о медленно затухающих колебаниях переходного процесса с частотой, близкой к частоте 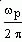 . Затухание этих колебаний тем меньше, чем острее и выше пик.
. Затухание этих колебаний тем меньше, чем острее и выше пик.
30. Синтез корректирующих устройств методом ЛАХ
32. Способы включения корректирующих устройств






