Выявление в механизме избыточных связей и их устранение

Для повышения надежности рекомендуется применять статически определимые механизмы, т.е. без избыточных (пассивных) связей. Такие механизмы называют рациональными. Избыточные связи – это связи, устранение которых не увеличивает подвижности механизма. Они вредны, так как увеличивают требования к точности изготовления звеньев, снижают надежность работы механизма.

Проверить механизм на наличие в нем избыточных связей можно путем подсчета их по структурным формулам, одна из которых предложена А. П. Малышевым: q=w+5p₅+4p₄+3p₃+2p₂+p₁-6n, где q – число избыточных связей; w – степень подвижности механизма; n – число подвижных звеньев; p₅ – число кинематических пар 5 -го класса; p₄ – число кинематических пар 4-го класса; p₃ – число кинематических пар 3 -го класса; p₂ – кинематические пары 2 -го класса; p₁ – кинематические пары 1-го класса.

Другую формулу предложил О. Г. Озол:

,

где к – число независимых контуров в механизме

;

h – суммарное число подвижностей, допускаемых кинематическими парами механизма .

При конструировании рационального механизма надо уметь определить, в каком замкнутом контуре имеются избыточные связи и какие они. При этом используется матричный метод определения структурных свойств механизма.

Матричное уравнение для определения избыточных связей механизма: 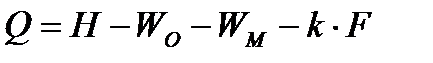, где 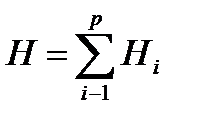; ; , Q – матрица избыточных связей механизма. Отрицательные элементы этой матрицы показывают избыточные связи, положительные – не выявленные подвижности; Н – суммарная матрица подвижностей в кинематических парах. W_O – суммарная матрица общих подвижностей; W_M – суммарная матрица местных подвижностей звеньев; n, p, m – число подвижных звеньев, кинематических пар и начальных звеньев в механизме; Н_i – матрица подвижности i – й кинематической пары, где переменные t_x, t_y, t_z показывают число поступательных подвижностей вдоль осей X,Y,Z.

Переменные r_x, r_y, r_z показывают число вращательных подвижностей вокруг осей X,Y,Z:

.

W_Oj – матрица общих подвижностей j –го начального звена (множество ее компонентов, равных единице, является подмножеством равных единице компонентов матрицы подвижностей кинематической пары, связывающей j – е начальное звено и стойку); W_Ml – матрица местных подвижностей l – го звена. F – единичная матрица замыкания контура (матрица подвижностей свободного твердого тела):

.

Для устранения избыточных связей следует заменить отсутствующие поступательные и вращательные подвижности имеющимися поступательными и вращательными подвижностями вдоль осей, не перпендикулярных направлениям отсутствующих подвижностей. Кроме того, отсутствующие поступательные подвижности необходимо заменить имеющимися в наличии вращательными.

Таким образом, в матрице подвижностей отрицательные элементы первого столбца могут быть заменены положительными элементами второго столбца, лежащими в других строках:

Для механизмов, в которых используются кинематические пары только 3, 4 и 5-го классов, можно использовать простое соотношение, облегчающее правильный выбор классов кинематических пар групп Ассура. Кинематическая группа не вносит избыточных связей при присоединии к механизму, если для нее выполняется соотношение:

, где и 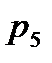– число кинематических пар третьего и пятого класса группы Ассура; - число местных подвижностей ее звеньев.

При получим: .

Данные соотношения будут выполняться и в том случае, когда все кинематические пары – четвертого класса, а местные подвижности звеньев отсутствуют. Приведенная зависимость позволяет правильно соориентироваться при выборе классов кинематических пар групп Ассура. Проверку структурных свойств полученного механизма и уточнение классов кинематических пар следует провести матричным методом.