Законы радиоактивного распада

Ранее было показано (раздел 2.4), что все ядра стремятся к устойчивости. Ядра, обладающие избытком протонов или нейтронов, становятся неустойчивыми в результате чего они распадаются на более устойчивые ядра. При этом происходит эмиссия из ядер (a-частиц, b-частиц) или происходит захват ядрами К-электронов и выделение энергии(в форме кинетической энергии частиц или g-квантов).

Нестабильность радиоактивных атомных ядер обусловлена их внутренним строением, и их распад происходит с определенной вероятностью. На современном уровне знаний мы не можем предсказать, за какое время распадется тот или иной атом.

В обычных лабораторных условиях на этот процесс не оказывают никакого влияния ни изменение температуры, ни повышение или уменьшение давления, ни магнитные, ни электрические поля. Скорость распада изменяется при непосредственном воздействии на атомные ядра (космическое излучение, бомбардировка быстрыми частицами), а также при очень высоких температурах.

Распады любых атомных ядер одного и того же нуклида равновероятны. Поэтому, если таких ядер достаточно много, общая скорость распада (т.е. число ядер dN, распадающихся за время dt) пропорциональна числу N атомов, имеющихся в наличии.

(3.1)

Коэффициент пропорциональности l называется постоянной распада, представляет собой долю распадающихся ядер в единицу времени dtи имеет смысл вероятности распада каждого отдельного ядра в единицу времени.

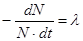(3.2)

Знак «-«говорит об уменьшении числа ядер. Иногда вместо постоянной распада пользуются обратной величиной, которую называют средним временем жизни и обозначают буквой t.

t= 1/ l (сек^-1).

Постоянная распада и соответственно среднее время жизни радиоактивного элемента зависит только от его порядкового номера и числа нуклонов и не зависит от его количества, поэтому она является одной из характеристик данного радиоактивного нуклида.

Выражение 3.1 представляет собой основной закон радиоактивного распада в дифференциальной форме..

Если нужно установить число радиоактивных ядер, не распавшихся (оставшихся) по истечении промежутка времени t, то пользуются интегральной формой основного закона распада, которую получают в результате интегрирования формулы (3.1), при условии, что в начальный момент времени t = 0, число ядер составляло N₀, тогда:

, или ln

и соответственно число оставшихся ядер (N_t) будет равно:

N_t = N_oe^-lt (3.3)

Экспоненциальный закон уменьшения со временем числа радиоактивных ядер представляет собой математическую запись того, что радиоактивный распад является спонтанным процессом, вероятность которого постоянна и не зависит от времени.

Если необходимо установить число распавшихся ядер к моменту времени t, то записывают:

N_р = N_o - N_t, или

N_р = N_o(1- e^-lt), (3.4)

где N_р- число распавшихся ядер к моменту времени t.