Міністерство освіти і науки України
Національний Авіаційний Університет
Кафедра загальної фізики
Лабораторна робота № 4
по темі:
“Визначення відношення молярних теплоємностей газів”
Виконав: студент групи КП-106
Допущений
Виконав
Здав
Київ – 2012
Мета роботи: дослідження адіабатичного процесу та ізопроцесів в ідеальних газах, визначення відношення молярних теплоємностей повітря.
Теоретичні відомості
Питома теплоємність с — скалярна величина, що чисельно дорівнює кількості теплоти, яку необхідно надати одиниці маси речовини, щоб збільшити її температуру на 1 К.
Молярна теплоємність С — скалярна величина, що чисельно дорівнює кількості теплоти, яку необхідно надати одному молю речовини, щоб підвищити його температуру на 1 К.
Молярна й питома теплоємності зв'язані між собою співвідношенням

де µ — молярна маса, тобто кількість речовини, виражена у грамах, що чисельно дорівнює відносній молекулярній масі.
Питома і молярна теплоємності газу залежать від умов, за яких проводиться нагрівання, тобто від характеру термодинамічного процесу. Наприклад, можна проводити нагрівання за сталого об'єму (V =const), або за сталого тиску (Р = const). При цьому завжди СР> Сv.
Формула Сp= Сv +R носить назву рівняння Майєра. З цього рівняння випливає, що Сpбільша за Сv на величину універсальної газової сталої.
Універсальна газова стала R чисельно дорівнює роботі ізобарного розширення одного молю ідеального газу при нагріванні його на один градус; R = 8,31 Дж / (моль • К).
Із молекулярно-кінетичної теорії випливає, що Сp і Сv залежній від числа степенів вільності і молекул, з яких складається газ:
 ,
,  .
.
Кількість степенів вільності молекули газу дорівнює числу незалежних координат, які необхідно задати для визначення положення молекули в просторі. Молекула одноатомного газу має три степені вільності (і = 3), жорстка молекула двохатомного газу — п’ять (i = 5), трьохатомного і багатоатомного — шість (i = 6).
Відношення теплоємності СР до Сv для ідеального газу називається показником адіабати. Для ідеального газу

Адіабатичним називається процес, який відбувається в системі без теплообмінуз навколишнім середовищем.
Закон Пуассона для адіабатичногопроцесу

формулюється так: для даної маси газу (m = const) добуток тиску газу на його об'єм, піднесений до степеня γ, є величиною сталою. Рівняння закону Пуассона можна подати також у змінних Р—T або V— Т:

За допомогою адіабатичного процесу з тим або іншим ступенем наближення можна розглядати широке коло практичних завдань, коли процеси в газах відбуваються досить швидко: вивчення протікання газу у вхідних пристроях компресорів, турбінах, соплах реактивних двигунів, аеродинамічний нагрів літальних апаратів.
Адіабатичний процес та ізопроцеси є окремими випадками так званого політропного процесу (процес за постійної теплоємності). Рівняння політропного процесу

де n може набувати значень від -∞ до +∞ залежно від виду процесу. Значення n для ізопроцесів наведено в табл. 4.
Таблиця 4
| Назва процесу | Значення n | Рівняння процесу | Теплоємність |
| Ізотермічний | T=const PV=const | CT=±∞ | |
| Ізохорний | ∞ | V=const P/T= const | 
|
| Ізобарний | P=const V/T=const | 
| |
| Адіабатичний | γ | PVγ=const | Cад=0 |
Метод та експериментальна установка
Експериментальний пристрій (рис. 35) складається із скляного балона 1 досить великої ємності, з'єднаного з рідинним U- подібним манометром 2. Верхня частина балона закрита кришкою і обладнана кранами 3 і 4, за допомогою яких балон сполучається з атмосферою і джерелом тиску 5 (у даному випадку гумова груша). Нехай у балоні початково був атмосферний тиск. Якщо швидко збільшити тиск у балоні й закрити кран 4, то кінцева різниця рівнів рідини в манометрі встановиться не одразу (при швидкому стисненні температура газу в балоні підніметься і пройде деякий час, поки температура повітря в балоні не зрівняється за рахунок теплопровідності з температурою навколишнього середовища).
Позначимо температуру навколишнього повітря T0, а тиск газу в балоні — Р1. Цей тиск дорівнює сумі атмосферного тискуРа і тиску Р', який визначається за показанням манометра:
Р1= Ра + Р'.

Стан газу, який характеризується параметрами P1, T0, назвемо першим станом газу. Відкриємо кран З, повітря розширюватиметься, доки його тиск не зрівняється з атмосферним і при цьому охолоне до температури Т2. Якщо в момент установлення атмосферного тиску в балоні кран 3 швидко закрити, то такий процес можна вважати адіабатичним. Параметрами Рa і Т2 буде визначатися другий стан газу. Повітря в балоні, яке охолонуло при адіабатичному розширенні, знову почне нагріватися. Цей процес нагрівання— ізохорний (бо кран закритий), при цьому температура повітря в балоні підвищиться до температури навколишнього середовища T0, а тиск зросте дозначення Р2. Це значення дорівнює сумі атмосферного тиску Рa і тиску Р', якому відповідає різниця рівнів стовпчиків рідини у манометрі h2:
Pa=Pa+P''
Параметри Р2 і T0 визначатимуть третій стан газу. Отже, ми маємо три стани газу, які характеризуються такими параметрами:
перший стан — T0, Pa+P';
другий стан — T2, Pa;
третій стан — Т0, Рa+ Р".
Розглядаючи газ як ідеальний, за допомогою рівнянь адіабатичного та ізохорного процесів запишемо вираз, який пов'язує параметри газу в трьох станах.
Адіабатичний процес (перехід із стану 1 у стан 2)

Ізохорний процес (перехід зі стану 2 у стан 3)

Поділивши рівняння адіабатичного процесу на рівняння ізохорного процесу та виконавши перетворення, дістанемо:

Прологарифмувавши цей вираз, маємо:

Оскільки згідно з умовою проведення дослідів

то вираз можна спростити, враховуючи, що за умови х «1 вираз
ln (1 + х)≈х, відповідно

Тоді маємо

Виразивши у із цього рівняння, дістанемо формулу
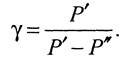
Тиск Р' у першому стані вимірюється різницею висот стовпців рідини у трубках манометра h1, а тиск Р", що відповідає показаннямманометра в третьому стані, вимірюється різницею висот h2, тому останній формулі можна надати вигляду

Ця формула є розрахунковою формулою цієї роботи.






