Применяется в сетях, в которых можно пренебречь индуктивным сопро-тивлением и учитывать только активные сопротивления. Например, в кабельных сетях напряжением до 35 кВ. Учитывая, что индуктивное сопротивление воздушных ЛЭП изменяется в малых пределах, прием может использоваться и для преобразования сетей более высокого напряжения.
Для упрощения расчетов сечения всех проводов сети приводятся с одному общему сечению. В качестве приведенной (эвивалентной) площади сечения принимается площадь сечения проводов, кторые наиболее часто встречаются в заданной сети. После приведения площадей сечений всех участков к эквива-лентной расчет преобразованной сети ведется не по сопротивлениям участков сети, а по их длинам. Это упрощает расчет.
В основу приема положено условие, что электрическое состояние сети до и после преобразования не изменяется. Это значит, что распеределение мощности и потеря напряжения одинаковы до и после преобразования.
Условие соблюдается, если активные сопротивления участков до и после преобразования не изменятся.
Предположим, что участок длиной l 1 выполнен сечением F 1. Сечение участка нужно заменить сечением F. Математически условие преобразования записывается следующим образом:
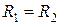или 
.
Для выполнения условия должна измениться длина участка сети. Ее величина определяется из приведенного выражения:
Прием 2. Замена параллельных линий при отсутствии на них нагрузок эквивалентной линией
Прямая задача. Известны мощности 
параллельных линий и их сопротивления 
(см. рис. 13.1 а). Необходимо найти значения 
и 
в преобразованной схеме (см. рис. 13.1 б).
Условие эквивалентности схем – одинаковое напряжение в точке 0 в преобразованной и исходной схемах.
Если напряжение в точках 1 – n одинаково, то мы можем записать:
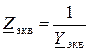и 
 |
Эквивалентная проводимость схемы рассчитывается по формуле:
Обратная задача. Известны мощность и сопротивление в преобразованной схеме (см. рис. 13.1 б). Найти мощности в исходной схеме (см. рис. 13.1 а).
Так как напряжение в точке 0 одинаково, то одинаково падение напряжения на сопротивлениях в преобразованной и исходной схемах:
или
Из полученного равенства можно найти значения мощностей :
… 
Прием 3. Замена источников напряжения, присоединенных к одной точке сети, одним эквивалентным
Прямая задача. Известны значения токов 
параллельных линий, их сопротивления и значения фазных ЭДС 
(см. рис. 13.2 а). Необходимо найти значения 
и 
в преобразованной схеме (см. рис. 13.2 б).
Условие эквивалентности схем – одинаковое напряжение в точке 0 в преобразованной и исходной схемах.
 |
Значение токов в ветвях исходной схемы рассчитываются по выражениям:
(13.1)
Значение тока в эквивалентной сети равно:
(13.2)
Подставим выражение (13.1) в (13.2):
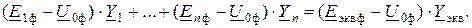
Так как 
, то полученное выражение можно записать так:
.
Раскроем скобки и выполним преобразования. В результате получим следующее выражение:
или
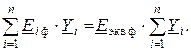
Откуда величина эквивалентной фазной ЭДС будет равна:
Обратная задача. Известны значения и в преобразованной схеме (см. рис. 13.2 б) Необходимо найти токов в исходной схеме. (см. рис. 13.2 а).
Величина падения напряжения на сопротивлениях в исходной схеме определяется как:
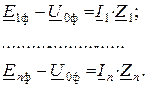
Аналогичное выражение можно записать для преобразованной схемы:
Из полученных выражений найдем значение напряжения в точке 0:
(13.3)
и
(13.4)
Приравнивая поочередно выражения из (13.3) к выражению (13.4), получим:
Из этих равенств можно определить искомые значения токов:
Чтобы определить значения мощностей в ветвях, нужно сопряженные комплексы токов умножить на значение напряжения в точке 0 и корень из трех:
Прием 4. Преобразование треугольника сопротивлений в эквивалентную звезду
Прямая задача. Известны значения мощностей в ветвях треугольника 
, их сопротивления 
. (см. рис. 13.3). Необходимо найти значения мощностей 
в лучах звезды и их сопротивления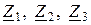 
.
Условие эквивалентности схем – режим за точками 1, 2 и 3 остается неизменным до и после преобразования.
Сопротивления лучей звезды рассчитываются по формулам:
Мощности в лучах звезды определяются по I закону Кирхгофа, составленного для узлов 1, 2, 3. При принятых направлениях мощностей получим:
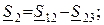
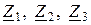Обратная задача. Известны значения мощностей в лучах звезды и их сопротивления (см. рис. 13.3). Необходимо найти значения мощностей в ветвях треугольника , их сопротивления .
Сопротивления сторон треугольника рассчитываются по формулам:
Мощности в ветвях треугольника рассчитываются по II закону Кирхгофа, составленного для замкнутых контуров. При принятом направлении обхода контуров по часовой стрелки, имеем следующие уравнения:
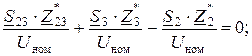
Решая полученные уравнения, определяем значения мощностей в треугольнике:
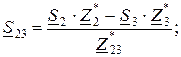
Прямым может быть преобразование звезды в треугольник. Тогда обратная задача – преобразование треугольника в звезду.
