1.1.Основні співідношення. Вивчається вплив, який здіснює деяка якісна ознака (фактор) на кількісний результат (відзив), наприклад, вплив технології виготовлення приладу на його довговічність, вплив способу обробки землі на урожайність і т.п. Нехай фактор має 
рівнів 
і хай величина x, що вимірюється є результатом дії фактора і випадкової складової e (що не залежить від фактора):
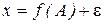
Будемо вважати, 1) що при кожному рівні 
фактора, j = 1,..., k, є 
вимірювань
i = 1,..., nj, (6.1)
де позначено 
, 2) що випадкова складова e нормально розподілена N (0, s2) з дисперсією s2. Якщо впливу фактора немає, то всі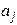 
рівні. Отож, є вибірок об’ємами n 1,..., nk, 
. Перевіримо гіпотезу про відсутність впливу:
H: a 1 = a 2 =...= ak
По кожній з вибірок методом найбільшої правдоподібності оцінимо середні aj і дисперсію s2:
, (6.2)
потім оцінимо s2 по всіх вибірках:
. (6.3)
Ця статистика незміщенно оцінює s2 незалежного від того, вірна чи ні гіпотеза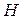 
.
Другу оцінку для s2 побудуємо по значеннях 
. Якщо 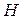вірна, то 
. Оцінки для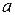 
і s2:
, 
(6.4)
З теореми про сумісний розподіл оцінок середнього і дисперсії нормальної сукупності витікає, що статистики (N - k)s2* і (k -1)s2** незалежні і розподілені як s2c2 N-k і 
відповідно, і тому їхнє відношення
, (6.5)
якщо гіпотеза 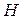вірна, має F -розпділ Фішера.
Якщо гіпотеза не вірна, то s2** має тенденцію до збільшення за рахунок розкиду середніх aj, і тому, якщо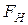 
має занадто велике значення, тобто якщо
, (6.6)
то гіпотеза 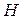про відсутність впливу фактора 
відхиляється, і необхідно вважати, що серед середніх a 1, a 2, …, ak є хоча б два не рівних; тут 
- квантиль рівня 
F- розподілу з 
і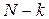 
ступенями свободи, a - вибираний рівень значущості. Якщо ж (6.6) не виконується, то це означає, що спостереження не суперечать гіпотезі про відсутність фактора. Умова (6.6) може бути записана інакше:
, (6.7)
де F - випадкова величина, розподілена за законом Фішера.
Оцінка впливу фактора. Відношення 
підкоряється розподілу Стьюдента з 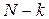ступенями свободи, і якщо Q = 
- квантиль рівня 1- a цього розподілу, то довірчий інтервал для aj з рівнем довіри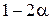 
:
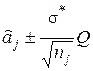(6.8)
Якщо гіпотеза 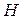про рівність середніх відхиляється, то слід визначити, по яких саме рівнях фактора середні значущо відрізняються. Лінійна комбінація
називається лінійним контрастом. Оцінка для L:
,
а оцінка дисперсії 
:
Зафіксуємо довільне число 
контрастів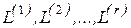 
. Можна показати, що одночасно для всіх 
виконуються співвідношення:
(6.9)
з ймовірністю 1-a. Це співвідношення дозволяє зробити висновок всі контрасти, що нас цікавлять одночасно. Зокрема, серед різниць aj – ai можна виділити ті, які значно відрізняються від нуля на вибраному рівні значущості (метод Шеффе).
Приклад. На заводі розроблено дві нові технології Т1 і Т2. Щоб оцінити, як зміниться денна продуктивність при переводі на нові технології, завод протягом 10 днів працював по кожній, включаючи існуючу Т0. Денна продуктивність в умовних одиницях наведена в табл. 1. Перевіримо гіпотезу про відсутність впливу технології на продуктивність.
таблиця 6.1
| № | Т 0 | Т 1 | Т 2 | № | Т 0 | Т 1 | Т 2 |
ПОСЛІДОВНІСТЬ ВИКОНАННЯ РОБОТИ
