5.1. Исходные числовые значения аргумента заданы цифрами, верными строгом смысле. Найти абсолютную и относительную погрешности функции. Определить количество верных цифр в строгом смысле по относительной погрешности в следующих элементарных функциях:
а) соs(0,47);
б) 
;
в) 
;
г) у = 1n (68,214).
Решение.
а) находим значение величины х. Оно будет равно 0,891568.
Абсолютная погрешность аргумента 
. Тогда абсолютная и относительная погрешности величины х равны:
;
Это означает, что в числе 0,891568 две цифры после запятой верны в строгом смысле.
Ответ: 0,892.
б) находим значение величины у. Оно будет равно 0,0450492.
Абсолютная погрешность аргумента 
. Тогда абсолютные и относительные погрешности величины у равны:
Это означает, что в числе 0,0450492 одна цифра после запятой верна в строгом смысле.
Ответ: 0,04.
в) Находим значение величины у. Оно будет равно 4,6378875.
Абсолютная погрешность аргумента 
. Тогда абсолютные и относительные погрешности величины у равны:
;
Это означает, что в числе 4,6378875 три цифры после запятой верны в строгом смысле.
Ответ: 4,6378.
г) Находим значение величины у. Оно будет равно 4,2226498
Абсолютная погрешность аргумента 
. Тогда абсолютные и относительные погрешности величины у равны:
.
Это означает, что в числе 4,2226498 пять цифр после запятой верны в строгом смысле.
Ответ: 4,222649.
5.2. Вычислить значение величины с помощью метода строгого учета границ абсолютних погрешностей после каждой операции:
, если а=12,34, b=14,3.
Решение.
При пооперационном строгом учете ошибок промежуточные результаты после округления до одной запасной (с учетом вычисленной параллельно величины погрешности) и их погрешности заносят в табл.
Расчетная таблица для вычисления погрешности выражения
| а | b | 
| 
| 
| ln(a) | b+ln(a) | A |
| 12,34 | 14,3 | 3,513 | 3,78 | 7,30 | 2,5129 | 16,81 | 0,434 |
| 
| 
| 
| 
| 
| 
| 
|
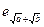
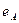
| 0,005 | 0,05 | 0,00071 | 0,0066 | 0,0073 | 0,0004 | 0,05041 | 0,0017 |
Значения погрешностей для удобства округлим до двух значащих цифр по избытку и тоже занесем в таблицу. Цифры даны верными в строгом смысле, значит, 
, 
.
Найдем 
. Абсолютная погрешность равна (воспользуемся табл. выше):
Из полученного значения погрешности видно, что в результате верны две значащие цифры после запятой, т. е.
.
Это число внесем в таблицу.
Найдем абсолютную погрешность 
= 3,781534.
Она будет равна 
Значит, в числе b будет одна верная цифра после запятой.
Аналогично, находим значения всех остальных действии и функции:
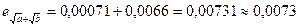
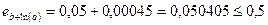
Округляя результат А до верной цифры, получаем окончательный ответ.
Ответ: А = 0,434 ±0,002.
6. Способ границ. Способ границ используется для точного определения границ искомого значения функции, если известны границы измерения ее аргументов.
6.1. Алюминиевый цилиндр с диаметром основания d=(3± 0,001) см и высотой h=(10±0,002) см весит р=(95,5±0,001) г. Определить удельный вес у алюминия и оценить предельную абсолютную погрешность найденного удельного веса.
Решение.
Способ.
Объем цилиндра равен: 
,
Отсюда 
.
Из полученной формулы вытекает, что в области р>0, d>0, h>0 функция 
– возрастающая по аргументу р и убывающая по аргументам d и h.
Имеем:
2,999 <d<3, 001;
9,998 < h < 10,002;
95,499< р < 95,501;
3,14159<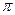 
<3,1416.
Тогда для значения у получим:
(нижняя граница)
(верхняя граница)
Взяв среднее арифметическое, получим значение у, равное у = (1,351 ±0,002) г/см3.
Ответ: у = (1,351 ±0,002) г/см3.
Способ.
Используя средние значения аргументов, получим:
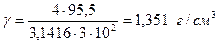
Логарифмируя формулу для вычисления объема цилиндра, имеем:
. Взяв полный дифференциал, получим:
.
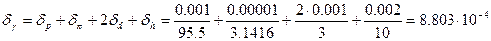
Далее находим:
.
Таким образом, имеем:
у = (1,351 ± 0,001) г/см3,
что очень близко совпадает с точной оценкой, найденной по способу границ.
Ответ: у = (1,351 ±0,001) г/см3.
6.2. Найти предельные абсолютную и относительную погрешности вычисления объема шара по выражению 
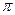, если d= 3,7±0,05 см, а = 3,14.
Решение.
Рассматривая d и 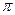как переменные величины, вычисляем частные производные:
Используя формулу для вычисления погрешности функции, зависящей от двух переменных:
,
Находим предельную абсолютную погрешность объема:
.
Поэтому,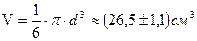 
.
Отсюда предельная относительная погрешность определения объема:
.
Ответ: 
, 
.
6.3. Для определения модуля Юнга Е по прогибу стержня прямоугольного сечения применяется формула 
, где l – длина стержня; а и b – измерения поперечного сечения стержня; s – стрела прогиба; р – нагрузка. Вычислить предельную относительную погрешность при определении модуля Юнга E, если р=20 кг; 
, а=3 мм; 
; b=44 мм; 
; l=50 см; 
; s=2,5 см;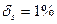 
.
Решение.
.
Отсюда, заменяя приращения дифференциалами, будем иметь:
. Следовательно,
.
Таким образом, относительная погрешность составит не более 0,081, т.е. примерно 8% от измеряемой величины.
Ответ: 
.
6.4. Вычислить значение величины z с помощью Mathcad при заданных значениях а, b и с с систематическим учетом абсолютных погрешностей после каждой операции, если цифры верны в строгом смысле.
, а:=12,34; b:=14,3
Решение.
Алгоритм решения представлен на рисунках, приведенных ниже:
