Особенности молекулярного строения жидкостей

Лабораторная работа № 6

«Определение коэффициента поверхностного натяжения методом Ребиндера»

Цель работы: Используя измерительную установку определить коэффициент поверхностного натяжения. Рассмотреть сущность физического явления поверхностного натяжения.

.

 

Вопросы теории (исходный уровень):

Сущность физического явления поверхностного натяжения. Коэффициент поверхностного натяжения и методы его определения. Капиллярные явления, их значение в биологических системах. Газовая эмболия.

(самостоятельная подготовка)

 

Содержание занятия:

1. Выполнить работу по указаниям в руководстве к данной работе.

2. Оформить отчет.

3. Защитить работу с оценкой.

4. Решить задачи.

 

Задачи.

1. Чему равен коэффициент поверхностного натяжения скипидара, если с помощью пипетки, диаметр кончика трубки которой 1,2 мм, его можно дозировать каплями по 0,01 г?

2. При переливании крови капельным методом необходимо было поддерживать частоту 40 капель в минуту. Какого диаметра должен быть кончик трубки капельницы, чтобы 250 мл крови перелить за 1,5 ч?

3. 3. В кровеносном сосуде образовался пузырек воздуха. В результате течения крови пузырек воздуха деформировался, образовав поверхности с радиусами кривизны 0,1 и 0,5 мм. Определить дополнительное давление в сосуде, возникающее в результате деформации пузырька воздуха.

4. В кровеносном сосуде образовалась цепочка из четырех пузырьков воздуха. Под действием давления крови р пузырьки деформировались, образовав поверхности с радиусами кривизны R, r₁ и r₂ (r₁ = r₂ = r; R > r). Определить дополнительное давление, обусловившее закупорку сосуда.

5. Определить плотность воздуха в пузырьке радиусом 5× 10^{-3 мм} , находящемся в артерии, давление крови в которой равно 100 мм рт. ст., а температура 37⁰ С. Атмосферное давление считать нормальным.

 

Лабораторная работа № 6.

«Определение коэффициента поверхностного натяжения методом Ребиндера»

Приборы и принадлежности: 1) установка для определе­ния поверхностного натяжения; сосуды объемом 50 см³ с дистиллированной во­дой, растворы хлорида натрия.

Силы, действующие на молекулы поверхностного слоя со стороны молекул, расположенных ниже этого слоя, значи­тельно превосходят силы, действующие на поверхностный слой со стороны молекул воздуха. Поэтому молекулы поверх­ностного слоя втягиваются внутрь жидкости. Для перемеще­ния молекул из жидкости на ее поверхность требуется совер­шить работу, т. е. поверхностный слой обладает потенциаль­ной энергией. Любое изменение поверхности требует затрат энергии, называемой поверхностной. Работа, требуемая для образования единицы такой поверхности, называется поверх­ностным натяжением а и измеряется в системе СИ в Дж/м². Поверхностный слой жидкости всегда ограничен линией воз­можного разрыва и находится под действием указанных сил в постоянном натяжении, стремящемся сократить поверх­ность. Сокращение поверхности возможно при условии, если силы поверхностного натяжения будут касательны к поверх­ности и перпендикулярны к линии возможного разрыва. От­сюда следует второе определение: коэффициент поверхност­ного натяжения а равен силе, рассчитанной на единицу дли­ны линии возможного разрыва. Единицы его измерения в си­стеме СИ — Н/м, в СГС — дин/см. Анализ размерностей по­казывает равнозначность этих единиц: Дж/м² = Н • м/м² = Н/м.

Поверхностное натяжение является важнейшей характе­ристикой поверхности раздела фаз. Под действием поверх­ностного натяжения небольшие количества жидких сред стре­мятся принять шарообразную форму, соответствующую наи­меньшей величине поверхности. Приближение к шаровой форме достигается тем больше, чем слабее силы тяжести. У малых капель сила поверхностного натяжения значительно превосходит силу тяжести. С поверхностным натяжением связаны диспергирование (измельчение, распыление) твердых тел и жидкостей на малые частицы или капли, коалесценция (слияние капель или пузырьков в эмульсиях, туманах, пе­нах), коагуляция (агрегирование частиц дисперсной фазы). Все эти явления связаны с образованием новых поверхностей, требующим затраты энергии.

Капиллярные явления также объясняются поверхностным натяжением. Поверхностное натяжение определяет форму клеток и их частей. Изменение сил поверхностного натяже­ния влияет на фагоцитоз (захват клетками соседних частиц), пиноцитоз (захват клеточной поверхностью жидкости с со­держащимися в ней ществами). Поверхностное натяжение различных веществ колеблется от 10 до 2000 эрг/см², у кле­ток оно не превышает 100 эрг/см². С ростом температуры по­верхностное натяжение уменьшается и при критической тем­пературе обращается в нуль. Растворенные в жидкости ве­щества способны как понижать, так и несколько повышать поверхнЪстное натяжение. Растворенные вещества, понижа­ющие поверхностное натяжение жидкости, называют поверх­ностно-активными веществами (ПАВ).

 

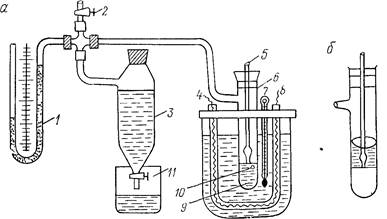
Рис. 18

Существует несколько способов определения поверхностного натяжения жидкостей. В данной работе описан метод определения максимального давления в пузырьке, который состоит в следующем.

В исследуемую жидкость 9, находящуюся в сосуде 6 (рис. 18,а), вертикально опускается капиллярная трубка 5, узкий конец которой диаметром не больше 0,5 мм касается

мениска исследуемой жидкости. Другим концом эта трубка сообщается с атмосферным воздухом. При закрытом кране 2 и открытом кране 11 вытекающая из сосуда 3 вода понижает давление над исследуемой жидкостью. При некотором давле­нии р над поверхностью исследуемой жидкости из конца ка­пиллярной трубки 5 под действием разности атмосферного давления р_о и давления р выдавли­вается в жидкость воздушный пузы­рек 10.

Рис. 19

Разность давлений р_о-р измеряемая манометром, равна pgΔh, где ρ— плотность манометрической жидкости, Δh—разность ее уровней. Разность давлений уравновеши­вается давлением р₁, обусловленным поверхностным натяжением жидкос­ти и гидростатическим давлением р₂. Так как глубина погружения кончи­ка капилляра мала, то р₂~0. Тогда давление, возникающее под действи­ем сил поверхностного натяжения, равно разности давлений, измеряемой манометром 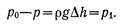1:

 

(1)

 

Найдем давление p₁. Рассечем произвольно пузырек воздуха радиусом R горизонтальной плоскостью на две части (рис. 19). Граница раздела — окружность радиусом r: В результате действия сил поверхностного натяжения верхняя часть пузырька притягивается нижней. При этом на каждый элемент длины dl пограничной линии действует сила dF = adl, направленная по касательной к поверхности пузырька. Най­дем элементарную силу давления:

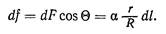
Интегрируя эту величину по всей длине пограничной линии, получим полную силу нормального давления:

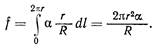
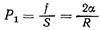(2)

Так как сечение выбрано произвольно, то расчет давления справедлив в любой точке пузырька. Из формулы (2) видно, что давление р₁ может быть большим в капиллярах малого радиуса. Из формул (1) и (2) следует, что

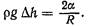(3)

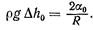(4)

Если вместо исследуемой жидкости в сосуд б налить эта­лонную жидкость, например дистиллированную воду, коэффи­циент поверхностного натяжения а которой известен, то мож­но записать

Разделив уравнение (3) на (4) и решив его относительно а, получим выражение для определения поверхностного натя­жения исследуемой жидкости

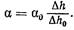
В медицинской практике часто приходится определять по­верхностное натяжение на границе двух несмешивающихся жидкостей. Поверхностное натяжение в данном случае удоб­нее всего определять методом максимального давления в пузырьке: капиллярную трубку 5 погружают так, чтобы узкий конец ее касался поверхности раздела двух несмешивающихся жидкостей (рис. 18, б). В этом случае следует учитывать гид­ростатическое давление жидкости, расположенной сверху, ко­торое не будет равным нулю.

Порядок работы

Определение поверхностного натяжения раствора хлорида натрия. Налив в сосуд дистиллированной воды при комнатной температуре, находят Δh₀. Затем наливаем в сосуд 5%-ый раствор хлорида натрия, находим Δh_c. По табличным значениям а ₀ и найденным величинам Δh₀ и Δh_c определяют а _c. Повторяем опыт для 10%, 15%, x% растворов. Полученные данные заносятся в таблицу 1. При комнатной температуре можно исследовать зависимость, а _c от концентрации раствора и убедиться в том, что с ростом концентрации хлорида натрия коэффициент поверхностного натяжения а _cувеличивается. По построенному градуировочному графику, графическим методом найдите неизвестную концентрацию x% раствора.

 

Таблица 1

Определяемые величины	Примечания
Δhc									a0	Δh0t
a c

 

 

Особенности молекулярного строения жидкостей

Обычные жидкости изотропны, структурно они являются аморфными телами. Для внутреннего строения жидкостей харак­терен ближний порядок в расположении молекул (упорядоченное расположение ближайших частиц). Расстояния между молекула­ми невелики, силы взаимодействия значительны, что приводит к малой сжимаемости жидкостей: небольшое уменьшение расстоя­ния между молекулами вызывает появление больших сил межмо­лекулярного отталкивания.

Подобно твердым телам, жидкости мало сжимаемы и обладают большой плотностью, подобно газам, принимают форму сосуда, в котором находятся. Такой характер свойств жидкостей связан с особенностями теплового движения их молекул. В газах молеку­лы движутся беспорядочно, на малых отрезках пути — поступа­тельно, в расположении частиц отсутствует какой-либо порядок. В кристаллических телах частицы колеблются около определен­ных положений равновесия — узлов кристаллической решетки. По теории Я. И. Френкеля молекулы жидкости, подобно части­цам твердого тела, колеблются около положений равновесия, од­нако эти положения равновесия не являются постоянными. По истечении некоторого времени, называемого временем «оседлой жизни», молекула скачком переходит в новое положение равно­весия на расстояние, равное среднему расстоянию между соседни­ми молекулами.

Вычислим среднее расстояние между молекулами жидкости. Можно мысленно представить весь объем жидкости разделенным на небольшие одинаковые кубики с ребром 5. Пусть в среднем в каждом кубике находится одна молекула. В этом случае 5 можно рассматривать как среднее расстояние между молекулами жид­кости. Объем жидкости равен V = &³N, где N — общее количество молекул жидкости. Если п — концентрация молекул (количество молекул в 1 м³), то N = nV. Из этих уравнений получаем

(7.18)

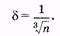
Порядок величины 6 составляет 10 ¹⁰ м, например, для воды 5 = 3 -10-¹⁰м.

.

Среднее время «оседлой жизни» молекулы называют време­нем релаксации т. С повышением температуры и понижением дав­ления время релаксации сильно уменьшается, что обусловливает большую подвижность молекул жидкости и меньшую ее вязкость.

Для того чтобы молекула жидкости перескочила из одного по­ложения равновесия в другое, должны нарушиться связи с окру­жавшими ее молекулами и образоваться связи с новыми соседя­ми. Процесс разрыва связей требует затраты энергии Е_а (энергии активации), выделяемой при образовании новых связей. Такой переход молекулы из одного положения равновесия в другое яв­ляется переходом через потенциальный барьер высотой £_а. Энергию для преодоления потенциального барьера молекула по­лучает за счет энергии теплового движения соседних молекул. За­висимость времени релаксации от температуры жидкости и энер­гии активации выражается формулой, вытекающей из распреде­ления Больцмана (см. § 2.4).

(7.19)

где т₀ — средний период колебаний молекулы около положения равновесия.

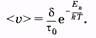
Зная среднее перемещение молекулы, равное расстоянию меж­ду молекулами 5, и среднее время т, можно определить среднюю скорость движения молекул в жидкости:

(7.20)

Эта скорость мала по сравнению со средней скоростью движе­ния молекул в газе. Так, например, для молекул воды она в 20 раз меньше, чем для молекул пара при той же температуре.

Поверхностное натяжение

На поверхностях раздела жидкости и ее насыщенного пара, двух несмешиваемых жидкостей, жидкости и твердого тела воз­никают силы, обусловленные различным межмолекулярным вза­имодействием граничащих сред.

Каждая молекула, расположенная внутри объема жидкости, равномерно окружена соседними молекулами и взаимодействует с ними, но равнодействующая этих сил равна нулю. На молекулу, находящуюся вблизи границы двух сред, вследствие неоднород­ности окружения действует сила, не скомпенсированная другими

молекулами жидкости. Поэтому для переме­щения молекул из объема в поверхностный слой необходимо совершить работу.

Поверхностное натяжение (коэффициент поверхностного натяжения) определяется от­ношением работы, затраченной на создание некоторой поверхности жидкости при посто­янной температуре, к площади этой поверхно­сти:

(7.21)

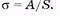
Условием устойчивого равновесия жидкостей является мини­мум энергии поверхностного слоя, поэтому при отсутствии внеш­них сил или в состоянии невесомости жидкость стремится иметь минимальную площадь поверхности при данном объеме и прини­мает форму шара.

Поверхностное натяжение может быть определено не только энергетически. Стремление поверхностного слоя жидкости сокра­титься означает наличие в этом слое касательных сил — сил по­верхностного натяжения. Если выбрать на поверхности жид­кости некоторый отрезок длиной I (рис. 7.8), то можно условно изобразить эти силы стрелками, перпендикулярными отрезку.

Поверхностное натяжение равно отношению силы поверхност­ного натяжения к длине отрезка, на котором действует эта сила:

(7.22)

Из школьного курса физики 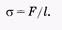известно, что оба определения, (7.21) и (7.22), тождественны. Приведем значения поверхностно­го натяжения для некоторых жидкостей при температуре 20 °С (табл. 15).

 

Таблица 15

 

Жидкость	а, Н/м	Жидкость	а, Н/м
Вода	0,0725	Ртуть	0,47
Желчь	0,048	Спирт	0,022
Молоко	0,05	Сыворотка крови	0,06
Моча	0,066	Эфир	0,017

Поверхностное натяжение зависит от температуры. Вдали от критической температуры значение его убывает линейно при уве­личении температуры. Снижения поверхностного натяжения можно достигнуть введением в жидкость поверхностно-активных веществ, уменьшающих энергию поверхностного слоя.