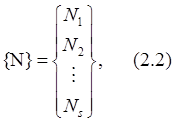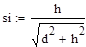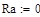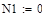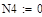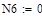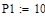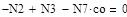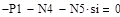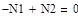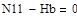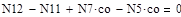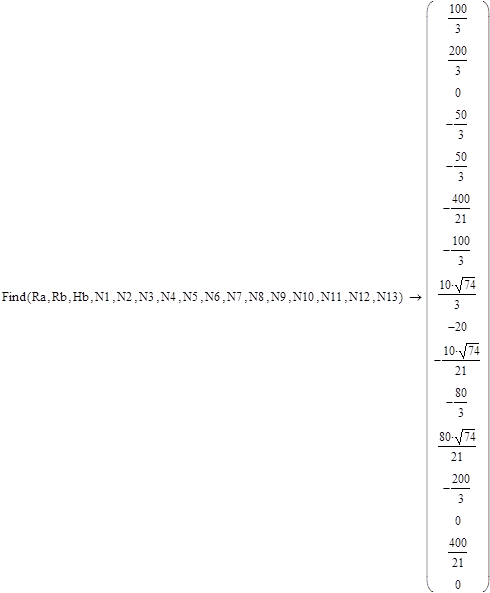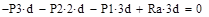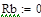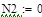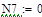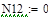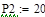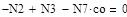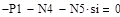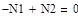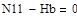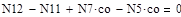Использование матриц влияния в расчетах ферм

Лабораторная работа № 2

Цель работы: изучить использование матриц влияния на примере расчета статически определимых ферм.

Порядок выполнения работы:

1) составить матрицу влияния для заданной фермы;

2) рассчитать усилия фермы с единичной нагрузкой во всех узлах фермы, а также рассчитать 2–4 примера с различной заданной нагрузкой (симметричной и несимметричной;

3) для всех примеров сделать рисунки с изображением полученных внутренних усилий в ферме;

4) сравнить полученные результаты расчета с результатами, полученными с помощью методики расчета фермы лабораторной работы № 1;

5) сделать выводы (проанализировать в каких стержнях возникает наибольшее усилие).

Методика расчета. При проведении расчетов, ориентированных на компьютерные технологии, в строительной механике применяют дискретные расчетные схемы и методы матричного исчисления [1]. Для примера такого подхода рассмотрим расчет фермы с помощью матрицы влияния продольных усилий.

Действующие на ферму нагрузки представим в виде вектора нагрузок (2.1), компонентами которого являются значения заданных нагрузок (P₁..P_t), пронумерованных в определенном порядке. Результатом расчета будет служить вектор усилий (2.2), в котором в заданном порядке будут перечислены значения продольных усилий в конкретных стержнях фермы (N ₁ ..N_s).

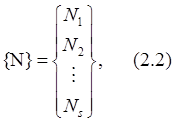
где t – количество действующих нагрузок; s – количество стержней фермы.

Матрица влияния продольных усилий фермы записывается в виде:

Каждый элемент n_ik матрицы влияния представляет собой величину продольного усилия в i -ом стержне фермы при действии на ферму только одной единичной нагрузки P_k = 1.

Вектор продольных усилий в стержнях фермы {N} будет определяться произведением матрицы влияния фермы [L_N] на вектор нагрузок {P}.

{N} = [L_N] ∙ {P}; (2.4)

Пример расчета. Для примера рассмотрим расчет фермы, рассмотренной ранее в лабораторной работе № 1 (рис. 2.1).

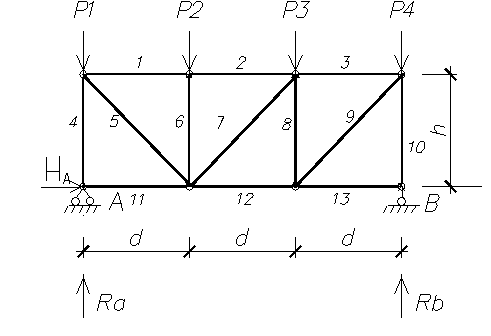
Рисунок. 2.1

Составим матрицу влияния фермы. Так как в данной ферме 13 стержней и к ней приложено 4 внешних силы, то матрица влияния будет иметь размеры
4 x13.

Для определения элементов n_i_,_k матрицы влияния данной фермы необходимо поочередно просчитать значения внутренних усилий в каждом i -ом стержне фермы при поочередном действии на ферму единичных нагрузок P_k =1, параллельно заполняя соответствующие столбцы матрицы влияния:

при P ₁=1; P ₂=0; P ₃=0; P ₄=0 (1 столбец);

при P ₁=0; P ₂=1; P ₃=0; P₄=0 (2 столбец);

при P ₁=0; P ₂=0; P ₃=1; P ₄=0 (3 столбец);

при P ₁=0; P ₂=0; P ₃=0; P ₄=1 (4 столбец).

Матрица влияния получится в следующем виде:

Используя полученную матрицу влияния, выполним примеры расчета фермы на различную нагрузку в системе компьютерной алгебры MathCAD:

а) при P ₁=1; P ₂=1; P ₃=1; P ₄=1;

б) при P ₁=10; P ₂=20; P ₃=30; P₄=40 (несимметричное нагружение);

в) при P ₁=10; P ₂=20; P ₃=20; P ₄=10 (симметричное нагружение);

Проанализировав результаты расчетов, можно сделать следующие выводы:

- наиболее растянутые стержни:

- № (N =) – при несимметричном нагружении, № (N =) – при симметричном нагружении;

- наиболее сжатые стержни – № (N =) – при несимметричном нагружении,

- № (N =) – при симметричном нагружении;

- сравнивая полученные результаты расчета с результатами, полученными с помощью методики расчета фермы лабораторной работы № 1, видим, что они совпадают.

Матрица влияния фермы

устанавливаем индексацию с 1 вместо 0 (по умолчанию)