Исходные данные: Массив А; Левая_граница (0); Правая_граница (n -1)
1. Индекс в начале, i = Левая_граница.
2. Индекс в конце, j =Правая_граница.
3. Опорный = A [(Левая_граница + Правая_граница) / 2].
4. Повторять
4.1. Движение слева направо:
Пока A[i ] < Опорный
i = i + 1
4.2. Движение справа налево:
Пока A[j ] > Опорный
j = j - 1.
4.3. Поменять местами A[i ] и A[j ].
4.4. i = i + 1.
4.5. j = j - 1.
Пока Левая_граница < Правая_граница.
5. Если Левая_граница < j, то отсортировать А от Левая_граница до j,
6. Если i > Правая_граница, то отсортировать А от i до Правая_граница.
7. Вывести массив А.
Сложность алгоритма зависит от выбора опорного элемента. Наилучшим считается значение так называемой медианы. Это – элемент, который меньше или равен половине элементов массива и больше или равен другой половине. Нахождение такого элемента требует выполнения дополнительных операций.
Число сравнений и пересылок при реализации быстрой сортировки в худшем случае пропорционально n2, т.е. его временная сложность равна О(n2), а в среднем и лучшем - О(n log n). Вообще рассмотренный метод является одним из наиболее эффективных, о чем говорит его название. Причем, наилучшие характеристики он обеспечивает для массивов, имеющих случайные значения.
3.4.3. Сортировка Боуза - Нельсона
Главным минусом предыдущих методов является удвоение размера памяти, первоначально занятой сортируемыми данными. Алгоритм Боуза – Нельсона является рекурсивным и не требует дополнительной памяти, т.е. упорядочение выполняется на месте исходного массива. Он основан на простой идее: слить две равные по размеру упорядоченные части можно слиянием их начальных, конечных половин, а также слиянием середин (2-й половины 1-го результата с 1-й половиной 2-го результата). Эта процедура иллюстрируется рисунком.
Если части не равны или не делятся точно пополам, процедуру уточняют соответствующим образом. Аналогично слияние «половинок» можно свести к слиянию «четвертушек», «восьмушек» и т. д. Таким образом, становится очевидной необходимость использования рекурсии.
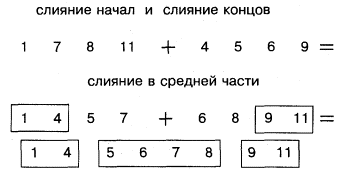 |
Рисунок. Иллюстрация слияния частей двух серий
Обозначим r - расстояние между началами сливаемых частей, m - их размер и j - наименьший номер элемента. Будем считать, что выполняется сортировка по возрастанию.
Рекурсивный алгоритм сортировки Боуза- Нельсона
1. Слияние
1.1. Начало рекурсии. Если j+r ≤ n, то
1.1.1. Если m = 1, то
a) Если A[j] > A[j+r ], то
Поменять местами A[i ] и A[j +r].
1.2. Иначе
1.2.1. m = m / 2.
1.2.2. Выполнить Слияние «начал» от j до m с расстоянием r.
1.2.3. Если j+r+m ≤ n, то
Выполнить Слияние «концов» от j+m до m с расстоянием r.
1.2.4. Выполнить Слияние «центральной части» от j+m до m с расстоянием m - r.
2. Основная часть рекурсии
2.1. m = 1.
2.2. Повторять
2.3. Цикл слияния списков равного размера
2.3.1. j = 1.
2.3.2. Пока j+m ≤n
1) Выполнить Слияние (j,m,m);
2) j = j + 2 m
2.3.3. Удвоение размера списка перед началом нового прохода
m = 2 m.
Конец цикла 2.2, реализующего все слияния
Пока m < n.
Число сравнений и пересылок при реализации сортировки методом Боуза - Нельсона в самом худшем случае пропорционально n log n, т.е. сложность алгоритма O(n log n). Дополнительная память, как уже отмечалось, не требуется.






