Точки, удаленные от плоскости на заданное расстояние, образуют плоскость, параллельную заданной плоскости. Чтобы построить ее надо найти хотя бы одну точку, удаленную от плоскости параллелограмма на расстоянии 40 мм.
Для этого надо восстановить перпендикуляр к плоскости параллелограмма, например, из вершины K.Для этого проводят в параллелограмме горизонталь и фронталь. Затем:
1).из горизонтальной проекции точки К проводят горизонтальную проекцию перпендикуляра перпендикулярно горизонтальной проекции горизонтали;
2). из фронтальной проекции точки К проводят фронтальную проекцию перпендикуляра перпендикулярно фронтальной проекции фронтали.
Перпендикуляр является прямой общего положения. Это значит, что по проекциям его откладывать отрезок заданной длины нельзя. Для того чтобы можно было это сделать, надо выбрать на перпендикуляре отрезок, произвольной длины. Для этого выберем на перпендикуляре произвольную точку Е. Получится отрезок ЕК (рис.15).

Далее ищут длину этого отрезка ЕК с помощью прямоугольного треугольника, на ней откладывают отрезок длиной 40 мм от точки К. Затем, возвращаясь к исходному чертежу, находят проекции точки, удаленной от параллелограмма на расстоянии 40 мм.
Построение плоскости треугольника, параллельного параллелограмму
В данной точке строят треугольник, стороны которого равны и параллельны сторонам параллелограмма, т.е. проекции сторон треугольника равны и параллельны одноименным проекциям сторон параллелограмма. Все построения приведены на рисунке 16.

Сторона RS равна и параллельна стороне NM параллелограмма, а сторона RT равна и параллельна стороне KN параллелограмма.
В случае, если плоскость построенного треугольника RST накладывается на плоскость параллелограмма, надо будет определять видимость треугольника по отношению к параллелограмму с помощью конкурирующих точек.
Задача № 4
Дана плоскость параллелограмма KLMN. Построить натуральную величину высоты параллелограмма.
Высота параллелограмма – это перпендикуляр, проведенный из одной из вершин параллелограмма на противоположную сторону.
Так как стороны параллелограмма – это прямые общего положения, то проводить прямую, перпендикулярную стороне на чертеже нельзя. Решение проводят через плоскость, перпендикулярную стороне параллелограмма.
1).Через одну из вершин параллелограмма проводят плоскость, перпендикулярную стороне параллелограмма. Для этого через вершину проводят горизонталь и фронталь перпендикулярно
стороне параллелограмма (рис.17).Выберем для этого вершину L.Проведем через эту точку горизонталь и фронталь, перпендикулярно стороне KN.

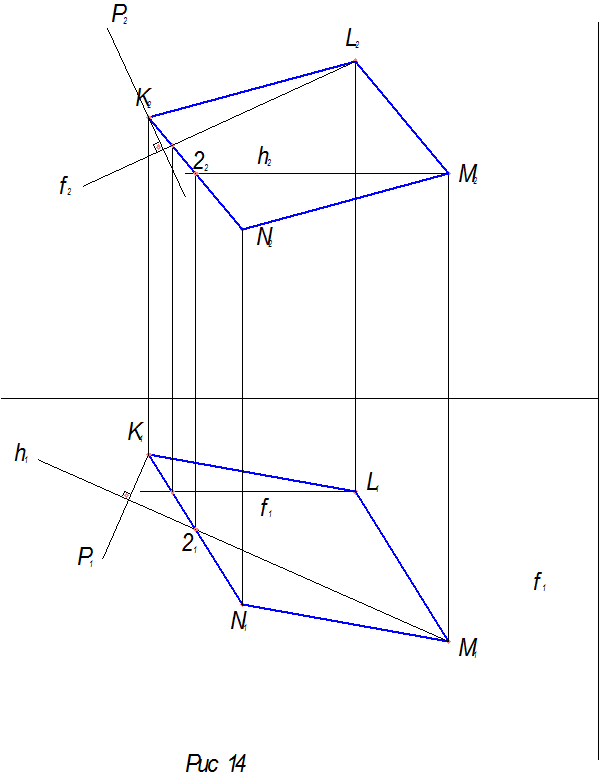
2).Далее ищут линию пересечения плоскости параллелограмма с плоскостью, заданной горизонталью и фронталью. Для этого вводят дополнительную проецирующую плоскость, которая пересекает обе заданные плоскости. Строят линии пересечения этих плоскостей с проецирующей плоскостью. Точка пересечения построенных прямых – это общая точка плоскости параллелограмма и плоскости, заданной горизонталью и фронталью. Соединив эту точку О с вершиной L, получаем линию пересечения плоскостей (рис. 18).

Эта линия является перпендикуляром, проведенным из вершины L параллелограмма на сторону KN, т.е. высотой параллелограмма. Эта высота является прямой общего положения, а следовательно надо найти натуральную величину высоты с помощью прямоугольного треугольника (рис.19).

.
ЗАКЛЮЧЕНИЕ
В данном методическом пособии разобраны все 4 задачи контрольной работы № 1.
Студентам предлагается решить задачи на отдельных чертежах, т.е. разместить контрольную работу не на одном листе формата А3,а на двух листах.






