Для решения задачи по построению линии пересечения плоскости треугольника АВС и параллелограмма KLMN задача по определению точки пересечения решается дважды,
так как необходимо определить две общие точки у плоскостей. Для этого находят точку пересечения одной из сторон треугольника с параллелограммом или стороны параллелограмма с треугольником. Затем выбирается другая сторона треугольника или параллелограмма и находится точка ее пересечения соответственно с параллелограммом или треугольником.
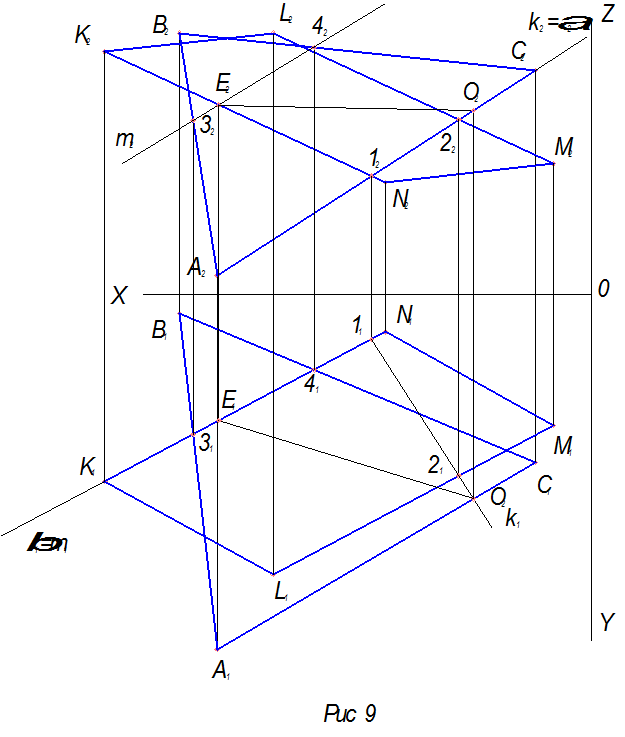
Так на рисунке 9 показано решение задачи по определению линии пересечения треугольника с параллелограммом. Решение проводится в следующем порядке:
1).Определяется точка пересечения стороны KN параллелограмма с плоскостью треугольника.
2). Определяется точка пересечения стороны АС треугольника с плоскостью параллелограмма.
После этого полученные точки соединяют и получают линию пересечения
плоскостей.
Определение видимости на чертеже
Завершает решение задачи определение видимости на чертеже. Видимость на чертеже определяется с помощью конкурирующих точек (рис.10).
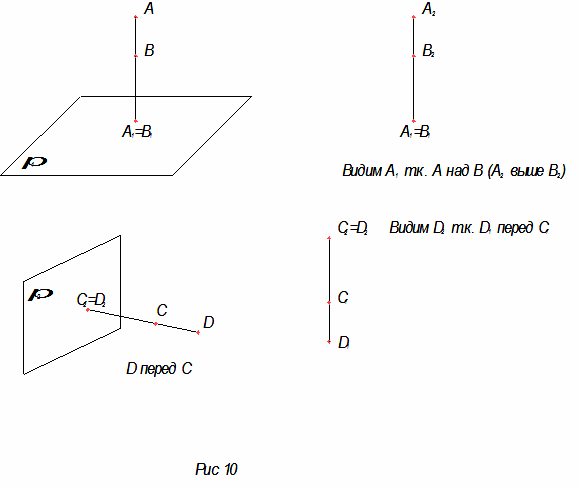
Конкурирующие точки – это точки, лежащие на одном проецирующем луче.
Рассмотрим две пары конкурирующих точек:
1).Горизонтально конкурирующие точки – это точки, лежащие на одном перпендикуляре к горизонтальной плоскости проекций. Следовательно, на горизонтальную плоскость они проецируются в одну точку. Из двух точек на горизонтальной плоскости будет видима та, которая выше по отношению к плоскости, а, следовательно, на чертеже ее фронтальная проекция лежит выше фронтальной проекции невидимой точки.
2). Фронтально конкурирующие точки - это точки, лежащие на одном перпендикуляре к фронтальной плоскости проекций. А, следовательно, на фронтальную плоскость они проецируются в одну точку. Из двух точек на фронтальной плоскости проекций будет видима та, которая дальше от плоскости, а, следовательно, на чертеже, ее горизонтальная проекция лежит перед горизонтальной проекцией невидимой точки.
Для определения видимости на чертеже эти пары точек выбираются так, что одна из них принадлежит плоскости треугольника, а другая плоскости параллелограмма. Анализируя положение проекций точек, определяют, которую из них видят, а, следовательно видят ту плоскость, чью точку видят.
Пример решения задачи
Пример решения задачи по построению линии пересечения плоскости треугольника с плоскостью параллелограмма приведен на рисунке 11.
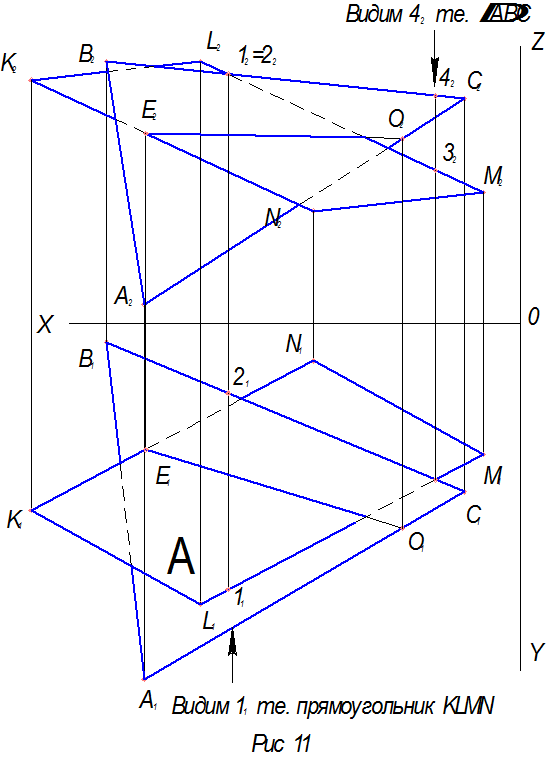
Для того чтобы не запутаться в построениях, можно выполнить решение в два этапа на двух разных чертежах. Затем их объединить в один чертеж. Но видимость определяется только на конечном чертеже (рис.11).
Задача№2
В этой задаче заданы плоскости треугольника и параллелограмма, смотри предыдущую задачу.
Надо построить ортогональную проекцию треугольника на плоскость параллелограмма.
Решение задачи основано на понятии перпендикулярности прямой и плоскости, так как для нахождения ортогональной проекции треугольника на плоскость параллелограмма необходимо построить ортогональную проекцию каждой вершины треугольника на плоскость параллелограмма.






