Тема: Анализ режимов цепей постоянного тока с использованием законов Ома и Кирхгофа

Цель: Научиться рассчитывать токи в ветвях с помощью законов Ома и Кирхгофа.

В результате выполнения практического занятия у студента формируются компетенции ПК-10 (умение проводить инженерные изыскания), ПК-17 (умение применять знание научно-технической информации, отечественного и зарубежного опыта по профилю деятельности).

Актуальность темы практического занятия заключается в необходимости использовать законы Ома и Кирхгофа для расчета электрических цепей.

Теоретическая часть

Закон Ома для участка цепи между зажимами a и b (рисунок 2.1) позволяет найти ток участка по разности потенциалов и сопротивлению этого участка:

. (2.1)

Рисунок 2.1 – Участок цепи

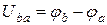Закон Ома для участка цепи между зажимами b и a (рисунок 2.2) позволяет найти ток участка по разности потенциалов и сопротивлению этого участка:

. (2.2)

Рисунок 2.2

Закон Ома для участка цепи содержащего ЭДС между зажимами a и b (рисунок 2.3 и рисунок 2.4).

Рисунок 2.3 – Участок цепи, Рисунок 2.4 – Участок цепи

содержащий ЭДС содержащий ЭДС

Для схем на рисунках 2.3 и 2.4 закон Ома позволяет найти ток участка по разности потенциалов , а также находящимся на этом участке ЭДС и сопротивлению .

Закон Ома для участка цепи, содержащего ЭДС (рисунке 2.3)

(2.3)

В случае если на участке цепи между зажимами a и b направление ЭДС будет противоположно току (рисунок 2.4).

(2.4)

Расчет режимов электрических цепей проводят используя первый и второй законы Кирхгофа.

Первый закон формулируется для узлов электрической цепи. Узлом называется место соединения трех и более ветвей электрической цепи. Ветвью электрической цепи называется участок электрической цепи между узлами, состоящий из одного или нескольких элементов по которым протекает один и тот же ток.

Первый закон Кирхгофа: алгебраическая сумма токов в узле электрической цепи равна нулю.

. (2.5)

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на элементах контура (под контуром здесь понимается замкнутая последовательность ветвей, не содержащих источников тока) равна алгебраической сумме ЭДС, действующих в этом же контуре:

или . (2.6)

Алгоритм решения задач с использованием законов Кирхгофа.

1. Определить количество узлов y и ветвей b электрической цепи.

2. Выбрать произвольно положительные направления искомых токов ветвей и обозначить их на схеме.

3. Определить количество уравнений по первому закону Кирхгофа, которое равно количеству узлов без единицы (y – 1). Записать для произвольно выбранных узлов требуемое количество уравнения по законам Кирхгофа. В алгебраической сумме следует учесть и токи источников тока.

4. Определить количество уравнений по второму закону Кирхгофа. Их число равно количеству ветвей без источников тока (b – b _ит) за вычетом уравнений, составленных по первому закону Кирхгофа, т.е. (b – b _ит) – (у – 1), где b _ит – число ветвей с источниками тока. Записать уравнения по 2-му закону Кирхгофа для независимых контуров. Независимые контуры образуются замкнутыми последовательностями ветвей, не содержащих источников тока, так, чтобы в новом контуре была хоть одна ветвь, не входящая в предыдущие. (Иногда в некоторых цепях необходимо составлять уравнения, в которые входят уже содержащиеся ветви.)

5. Объединить уравнения, составленные по первому и второму законам Кирхгофа, в систему уравнений.

6. Решить систему уравнений.

Пример использования алгоритма решения задач с использованием законов Кирхгофа для электрической цепи, представленной на рисунке 2.5.

Рисунок 2.5 – Схема электрической цепи

При расчетах как правило необходимо определить токи в ветвях схемы. Все параметры элементов электрической цепи, и ее топология считаются известными.

Решение.

1. Определим количество узлов y и ветвей b электрической цепи. Так, в рассматриваемой цепи имеется три узла, обозначенных цифрами 1, 2 и 3 всего y = 3. Ветви находятся между узлами и в представленной цепи их пять b = 5.

2. Выберем произвольно положительные направления искомых токов 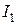, , , ветвей и обозначим их на схеме.

3. Определим количество уравнений по первому закону Кирхгофа, равное количеству узлов без единицы: 3 – 1 = 2. Запишем для произвольно выбранных узлов требуемое количество уравнений по первому закону Кирхгофа. В алгебраической сумме следует учесть и токи источников тока.

1 узел:

2 узел:

4. Определим количество уравнений по второму закону Кирхгофа, равное числу ветвей без источников тока (5 – 1) минус два уравнения, составленные по первому закону Кирхгофа, т.е. (5 – 1) – 2 = 2. Запишем уравнения по 2-му закону Кирхгофа для независимых контуров. Независимые контуры образуются замкнутыми последовательностями ветвей не содержащих источников тока.

Уравнения по второму закону Кирхгофа для рассматриваемой электрической цепи.

I контур: ,

II контур: .

5. Объединить уравнения, составленные по первому и второму законам Кирхгофа в систему уравнений.

(2.7)

6. Решить полученную систему уравнений можно, если в ней четыре неизвестные. Чаще всего в задачах требуется определить токи (т.е. для данной схемы 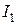, , , ), тогда все остальные элементы должны быть известными. Возможны и другие варианты.

Таким образом, получена система уравнений 2.7 для заданной электрической цепи рисунок 2.5 по законам Кирхгофа.

После расчета токов, необходимо проверить баланс мощностей электрической цепи.

Баланс мощностей в электрической цепи.

Общая мощность источников электрической энергии для электрической цепи (рисунок 2.5) определяется следующим образом:

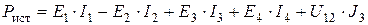. (2.8)

Знак «минус» в выражении (2.8) у мощности источника ЭДС 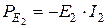, ставится потому, что направление тока противоположно направлению ЭДС . Если направление источника ЭДС и тока через него не совпадает, то данный источник ЭДС потребляет электрическую энергию, а не производит ее. Мощность источника тока , т.к. у источника тока потенциал 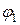больше, чем . Как определять потенциалы электрической цепи (напряжение на участке цепи), будет рассмотрено ниже в примере построения потенциальной диаграммы.

Общая мощность потребителей электрической энергии для электрической цепи (рисунок 2.5) определяется следующим образом:

. (2.9)

В результате расчетов общая мощность источников электрической энергии должна оказаться равна общей мощности потребителей электрической энергии 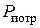для рассматриваемой электрической цепи . Если равенство не получается, значит, имеются ошибки в расчетах, которые требуется устранить.

Пример. Построение потенциальной диаграммы для внешнего контура электрической цепи, представленной на рисунке 2.5. Внешний контур состоит из элементов , , , , , . Перечень элементов производился от наибольшего по названию узла, в данном случае это узел 3, по часовой стрелке. Из рисунка видно, что при выборе контура в его состав не включены ветви с источником тока, т.к. его сопротивление равно бесконечности, и определить падение напряжения на нем по закону Ома не удастся. Обозначим на электрической схеме точки при переходе от одного элемента к другому. Так, между элементами и получим точку а, между и – точку b, между и обозначим точку с. Используя закон Ома, определим потенциалы всех указанных во внешнем контуре точек. Для этого условно заземлим потенциал точки 3, тогда станет равен нулю. При этом токораспределение в цепи не изменится, т.к. никаких новых ветвей, по которым могли бы протекать токи, не образуется.

Тогда потенциалы обозначенных в схеме точек при известных токах определятся следующим образом:

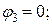
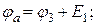
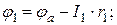
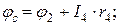
Знак «плюс» в формуле 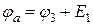ставится потому, что ЭДС повышает потенциал при переходе от потенциала к . Знак «минус» в формуле ставится потому, что ток течет от большего потенциала к меньшему . Чтобы определить меньший потенциал необходимо от большего вычесть падение напряжения на резисторе . Знак «минус» в формуле ставится потому, что ЭДС 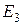понижает потенциал при переходе от потенциала к 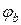. Знак «плюс» в формуле ставится потому, что ток течет от большего потенциала к меньшему . Чтобы отыскать больший потенциал необходимо к нему прибавить падение напряжения 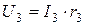на резисторе . Аналогичным образом ставятся знаки в других уравнениях потенциалов электрической цепи. Представленные формулы для определения потенциалов электрической цепи вытекают из закона Ома.

На основании полученных значений потенциалов точек строится потенциальная диаграмма 2.6.

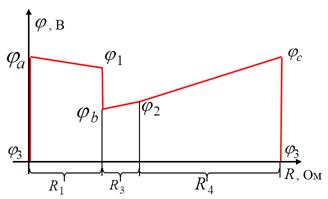
Рисунок 2.6 – Потенциальная диаграмма

Задания

1. Определить показание вольтметра для схемы, изображенной на рисунке 2.7. (15 В).

Рисунок 2.7

2. Определить токи в ветвях схемы рисунок 2.8, применяя законы Кирхгофа. Дано: = 3 В, = 2 В, = 2 В, = 1 В, = 1A, 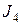= 0,5 A, = 4 Ом, = 6 Ом, = 2 Ом, = 8 Ом, 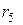= 10 Ом. ( 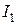= 0,2 A, = 0,7 A, = -0,5 A, = 0,1 A, = 0,1 A)

Рисунок 2.8

3. Для цепи рисунок 2.9 построить потенциальные диаграммы при разомкнутом и замкнутом ключе. Дано: = 15 В, = 5 В, = 20 В, = 35 В, = 8 Ом, = 24 Ом, = 40 Ом, = 4 Ом. Внутренние сопротивления источников энергии: 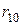= 2 Ом, = 6 Ом, = 2 Ом, = 4 Ом.

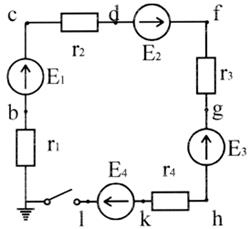
Рисунок 2.9

Контрольные вопросы

1. Записать закон Ома для участка эклектической цепи и для полной цепи.

2. Как определяется направление тока при известных потенциалах электрической цепи?

3. Дайте определение узлам и ветвям электрической цепи.

4. Сформулируйте и запишите первый закон Кирхгофа.

5. Сформулируйте и запишите второй закон Кирхгофа.

6. Как определить показания вольтметра по известным токах в ветвях?

7. Методика построения потенциальной диаграммы для замкнутого контура электрической цепи.

8. Поясните, как произвести учет внутреннего сопротивления источника энергии при построении потенциальной диаграммы.

 

Список литературы, рекомендуемый к использованию по данной теме

Основная литература

1. Немцов М.В. Электротехника и электроника (6-е изд., стер.) учебник. –М: Академия, 2013. – 480 с. – ISBN: 9785446804320.

2. Электротехника и электроника: Учебное пособие для вузов / В.В. Кононенко [и др.]; под ред. В.В. Кононенко. – Изд. 6-е – Ростов н/Д: Феникс, 2010. – 784 с. (Высшее образование). – ISBN 978-5-222-17568-2.

Дополнительная литература

3. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: Учебник. – 10-е изд. – М.: Гардарики, 2002. – 638 с.

Практическое занятие 3