Рассмотрим электрическую цепь по отношению только к источнику и исследуемой ветви – нагрузке. Сигнал, действующий на входе этой цепи, назовем внешним воздействием, сигнал на выходе – откликом или реакцией цепи. Необходимо определить реакцию цепи на внешнее воздействие.
 |
Пусть внешнее воздействие задано в виде тока или напряжения источника, а искомая реакция (отклик) представляет собой ток или напряжение нагрузки (рис. 7.1).
Рассмотрим случай гармонического внешнего воздействия. Обозначим х (t) – внешнее воздействие, у (t) – отклик. Так как воздействие и отклик изменяются гармонически, то мы можем представить их в виде комплексных амплитуд 
и 
.
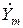Комплексной частотной характеристикой цепи (частотным коэффициентом передачи) называется отношение комплексных амплитуд отклика и воздействия
,
где 
, 
– действующие значения отклика и воздействия.
Размерность комплексной частотной характеристики (КЧХ) определяется отношением размерностей отклика и воздействия. Если отклик является напряжением, а воздействие – током, то КЧХ имеет размерность сопротивления; если отклик – ток, а воздействие – напряжение, то КЧХ – проводимость; если и отклик и воздействие являются током или напряжением, то КЧХ безразмерная величина.
Комплексную частотную характеристику, как и любое комплексное число, можно записать в показательной и алгебраической форме:
.
Здесь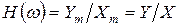 
– модуль комплексной частотной характеристики, равный отношению амплитуд или действующих значений отклика цепи и внешнего воздействия. 
– аргумент, представляющий собой разность фаз отклика и воздействия.
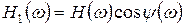– действительная часть КЧХ,
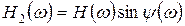– мнимая часть КЧХ.
Зависимость модуля КЧХ 
от частоты называется амплитудно-частотной характеристикой (АЧХ). Зависимость аргумента 
от частоты называется фазо-частотной характеристикой (ФЧХ).
Графически строят отдельно АЧХ и ФЧХ либо изображают зависимость от частоты действительной и мнимой частей КЧХ.
Комплексную частотную характеристику можно изобразить в виде одной зависимости – годографа КЧХ на комплексной плоскости (рис. 7.2).
 |
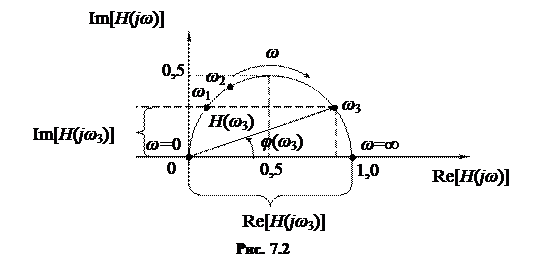Годограф – это геометрическое место концов вектора 
, соответствующих изменению частоты от 
до 
. На годографе указывают точки, соответствующие некоторым значениям частоты, и стрелкой указывают перемещение конца вектора 
при увеличении частоты.
Годограф дает представление как об АЧХ и ФЧХ, так и о частотной зависимости действительной и мнимой составляющих, поэтому его иногда называют амплитудно-фазовой частотной характеристикой (АФЧХ).
 |
Комплексная частотная характеристика называется входной (ВЧХ), если отклик у (t) и внешнее воздействие х (t) рассматриваются на одних и тех же зажимах цепи (рис. 7.3, а). Например, если х (t) = i (t) – ток на входе цепи, а у (t) = u (t) – напряжение на входе цепи, то ВЧХ – комплексное входное сопротивление по отношению к зажимам «аb»
.
Комплексная частотная характеристика называется передаточной (переходной), если отклик у (t) и внешнее воздействие х (t) рассматриваются на разных зажимах цепи (рис. 7.3, б). Например, отклик у (t) = ucd (t) – напряжение на выходе цепи, а внешнее воздействие х (t) = uab (t) – напряжение на входе цепи. В этом случае КЧХ представляет собой комплексный коэффициент передачи по напряжению
.
Коэффициент передачи – величина безразмерная.
