Кернеулердің потенциалдық диаграммасы

 

Потенциалды диаграмма электр потенциалының берілген тізбектің контурда таралғанын көрсетеді және келесі түрдегі тәелділік график түрінде болады.

 

j = f (R),

 

мұндағы j - таңдап алынған тізбектің контурының түйіндерінің потенциалдары;

R – осы контур бойымен резисторлардың кедергілерінің косындысы.

Потенциалды диаграмманы есептегенде және жерлендіргенде электрлік потенциалдың алғашқы түйіні 0- ге тең деп алынады. Контурды толық өткеннен кейін және алғашқы түйінге қайтып келгеннен кейін потенциал 0- ге тең болу керек.

Кернеудің потенциалды диаграммасын салғанда таңбалар ережелері келесідей:

- таңдап алынған контурдан өту кез- келген бағытта жүргізілуі мүмкін;

- контурды өту бағыты мен ЭҚК- нің бағыты сәйкес келсе, онда ЭҚК-тің мәні қосу(+) таңбасымен, ал кері жағдайда алу(-) таңбасымен жазылады.

- Контурды өту бағыты мен R резистордан өткен токтың оң бағытымен сәйкес келсе, онда U = R I кернеуінің түсуі алу(-) таңбасымен және қосу(+) таңбасымен кері жағдайда жазылады.

«c,a,e,d,f,c» контуры үшін потенциалды диаграмманы тұрғызайық. Алғашқы потенциал ретінде «c». Контурда өтудің бағытын сағат тіліне қарама- қарсы алайық.

 

j_c = 0

j_a = j_c – R₄ I₄ = 0 – 3 * 1.919 = - 5.757 B

j_e = j_a + E₂ – R₀₂ I₂ = - 5.757 + 42 – 0.4 * 3.507 = 34.84 B

j_d = j_e – R₂ I₂ = 34.84 – 4 * 3.507 = 20.81 B

j_f = j_d + R₃ I₃ = 20.81 + 5 * (- 0.83) = 16.66 B

j_c = j_f – E₃ + R₀₃ I₃ = 16.66 – 16 + 0.8 * (- 0.83) = - 0.0018 B» 0

 

8 – суретте кернеулердің потенциалдық диаграммасы тұрғызылған.

 

 

Қосымша 1.

 

Сызықты теңдеулер жүйесін Крамер формуласы бойынша шешу.

 

2- ші ретті сызықты алгебралық теңдеулер жүйесі келесі түрде

 

 

теңдеулер жүйесі матрицалық формада келесі түрде жазылады

А₁₁ А₁₂ Х₁ В₁

=

А₂₁ А₂₂ Х₂ В₂

немесе жалпы түрде

 

А Х = В

мұндағы [ X ] – матрица- белгісіздер шамасының бағаны,

 

[ B ] – матрица- бос мүшелер бағаны,

 

[ A ] – белгісіздер шамасы кезіндегі тұрақты коэффиценттерінің квадраттық матрицасы.

 

Крамер формуласы бойынша анықтауыштардықолдана отырып 2-ші ретті матрицалық теңдеулерді келесі түрде шешеміз

 

 

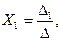
мұндағы – жүйенің басты анықтауышы.

Δ₁, Δ₂ – қосымша анықтауыштары.

 

Анықтауыштар келесі түрде анықталады

 

3- ші ретті алгебралық теңдеулер жүйесін шешу аналогикалық түрде жүргізіледі.

3- ретті теңдеулер жүйесі жәй және матрицалық түрде көрсетіледі

 

немесе

Крамер формуласы бойынша есептеу төмендегідей жазылады

 

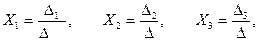
Мұндағы анықтауыштар тең болады:

 

 

 

Анықтауыштарды есептеу үшін программалаушы калькуляторды қолдануға болады.

 

 

РГЗ орындау үшін негізгі параметрлер варианты

 

 

№	Е1	R01	E2	R02	E3	R03	R1	R2	R3	R4	R5	R6
B	Ом	B	Ом	B	Ом	Ом	Ом	Ом	Ом	Ом	Ом
		0.8		0.4		0.6
		0.7		0.3		0.5
		0.4		0.2		0.8
		0.8		0.3		0.4
		0.4		0.6		0.7
		0.7		0.5		0.7
		0.6		0.8		0.5
		0.2		0.6		0.8
		0.7		0.1		0.3
		0.5		0.8		0.4
		0.6		0.1		0.8
		0.2		0.2		0.8
		0.1		0.6		0.2
		0.3		0.7		0.4
		0.2		0.3		0.4
		0.6		0.4		0.2
		0.5		0.1		0.8
		0.7		0.3		0.9
		0.1		0.5		0.8
		0.7		0.2		0.9

 

 

 

 

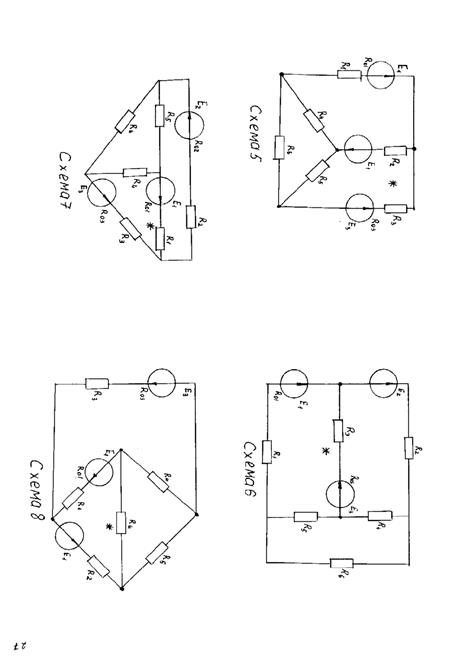
Тапсырма №2