АЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
М.х.дулати атындағы тараз мемлекеттік университеті
БЕКІТЕМІН
Кафедра меңгерушісі
т.ғ.к., профессор
Джунисбеков М.Ш.
______________________
/қолы/ /аты-жөні./
«_____»____________201__ж.
________________ Студенттердің өзіндік жұмысын ___________ орындау үшін
/жұмыстың атауы/
_________ Электрлік тізбектер теориясы_____________ ______ пәнінен
/пәннің атауы/
_ 5B071900_Радиотехника, электроника және телекоммуникация
/мамандық шифры/
мамандығының білімгерлері үшін
ДІСТЕМЕЛІК НҰСҚАУ
Тараз 2014
Әдістемелік нұсқау _______________________________________________
/тәжірибелік, зертханалық жұмыстың атауы/
орындау үшін
___________ Электрлік тізбектер теориясы _____________________________
/пәннің атауы/
_ 5B071900_Радиотехника, электроника және телекоммуникация __________
/мамандық шифры/
мамандығының білімгерлері үшін пәннің типтік оқу бағдарламасына сәйкес жасалған.
Әдістемелік нұсқауды құрастырушылар:
__ Тлешова А.С. ________
/аты-жөні/ /қолы/
Әдістемелік нұсқау __ Автоматика және телекоммуникация _________
/кафедра атауы/
кафедра мәжілісінде талқыланды
Хаттама №_____ «______»_____________20__ж.
Тұрақты токтағы электр тізбегіне анализ жасау.
Тапсырма № 1
Тұракты токтың сызықты электр тізбегінің анализін кернеудің үш нақты көзі арқылы жүргізу:
1. Тармақтағы токтарға қатысты Кирхгофтың заңдары бойынша, тізбектің электрлік күйінің теңдеулер жүйесін құру.
2. Контурлық ток әдісі көмегімен барлық токтарды есептеп шығару.
3. Түйіндік кернеу әдісімен (екі түйін әдісі) тізбектегі барлық тармақтардағы токтарды анықтау, сонымен қатар кедергілер үшбұрышын эквивалентті кедергілер (R4,R5,R6 резисторлары) жұлдызшасына ауыстыру жолымен берілген схеманы алдын-ала түрлендіру керек.
4. R6 резисторы арқылы ағатын токтың мәнін балама генератор әдісімен анықтау.
5. Вольтметрдің көрсетулерін анықтап, берілген схема үшін қуаттар балансын құру.
6. Электр тізбегінің белгіленген контуры үшін кернеулердің потенциалды? диаграммасын есептеу және салу (* белгіленген).
Мысал:
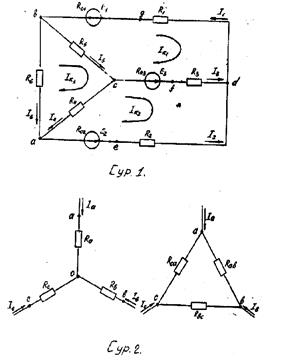
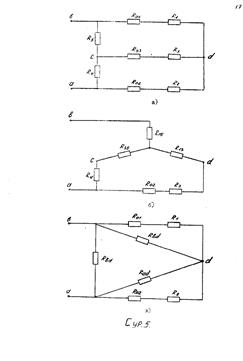
1-ші суретте электр тізбегінің схемасы берілген, ал оның элементтер параметрі төмендегідей:
E1=6 B; E2=42 B; E3=16 B;
R01=0.2 Oм; R02=0.4 Oм; R03=0.8Ом;
R1=9 Oм; R2=4 Oм; R3=5 Oм;
R4=3 Oм; R5=2 Oм; R6=5 Oм.
Электр тізбегі алты тармақтан және төрт түйінен тұрады. Нақты кернеу көзі екі параметрмен сипатталады: Э.Қ.К. Е мәні және R0 ішкі кедергі көзінің шамасымен. Нақты көздің орынбасу схемасы Е идеал кернеу көзі мен R0 резистордың тізбектей қосылуын көрсетеді.
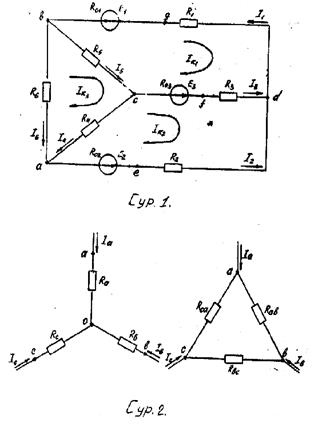
Айтарлықтай, электр тізбегінде жүргізілетін анализдің мақсаты тізбектегі элементтердің мәндері және оларды қосу тәсілдері бізге белгілі болғандықтан барлық немесе кейбір тармақтардағы токтардың және кернеулердің мәндерін анықтаудан тұрады. №1 есептің тапсырмасына сәйкес түрлі әдістермен электр тізбегіне анализ жүргіземіз (1-сурет).
1. Кирхгоф заңдарын қолдану әдісі.
Кирхгоф заңдары келесі түрде тұжырымдалады:
а) Кирхгофтың бірінші заңы немесе Кирхгофтың токтар заңы (КТЗ) -электр тізбегіндегі түйіндегі токтың алгебралық қосындысы 0-ге тең немесе түйіндегі кірген токтың қосындысы шыққан токтардың қосындысына тең.
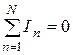
б) Кирхгофтың екінші заңы немесе Кирхгофтың кернеулер заңы (ККЗ)- тұйықталған электр тізбегіндегі ЭҚК-нің алгебралық қосындысы сол тұйықталған тізбектегі кедергілерге түскен кернеулердің алгебралық қосындысына тең.
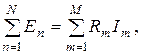
мұндағы: U=RI түсінігі, R резисторындағы кернеудің түсіу деп аталады.
Кирхгофтың заңдар негізінде жазылған тармақтардағы токтарға қатысты, тізбектің электрлік күйінің теңдеулер жүйесі тәуелсіз болады, егер КТЗ бойынша – (n-1)-теңдеуі, ал ККЗ бойынша – (m-(n-1))- теңдеуі құрылса, мұндағы m-тармақ саны, n-түйін саны.
Кирхгофтың заңдары бойынша теңдеуді құрған кезде төмендегі ережелерді қолдану керек.
1. КТЗ белгілерінің ережесі:
- электр тізбегінің түйініне кіретін токтар оң (+) таңбасымен алынады, ал түйіннен шығатын токтар теріс (-) таңбасымен алынады.
2. ККЗ белгілерінің ережесі:
- контурлық токтың бағытын өз қалауымызша аламыз;
- егер ЭҚК- тің бағыты контурлық токтың бағытымен сәйкес келсе, онда ЭҚК-тің бағыты оң болады. Ал керісінше жағдайда теріс болады;
- егер кедергілерден өткен ток контурлық ток бағытымен сәйкес келсе, онда кедергіден өткен кернеу RI таңбасы оң болады, ал керісінше жағдайда теріс болады.
Кирхгофтың заңдары бойынша тізбектің электрлік күйінің теңдеуінің алгоритмі келесі түрде болады:
1. Талданатын электр тізбегінің m тармақтар саны және n түйіндер саны анықталады, оларды сандармен немесе әріптермен белгілейміз.
2. Тізбектің барлық тармақтарындағы токтардың бағытын өз қалауымызша белгілейміз, бұл схемада көрсетілген, олай болса, бізде тармақтардағы m белгісіз токтар пайда болады.
3. КТЗ бойынша (n-1) теңдеуі құрылады.
4. Тәуелсіз контурлар үшін ККЗ бойынша (m-(n-1)) теңдеуі жазылады. Контурлар тәуелсіз деп аталады, егер ол ең болмағанда бір тармақпен ажыратылса. Қарапайым жазық схемалар үшін ұяшық контур түсінігін қолданған қолайлы. Ұяшық бұл – тізбектің контуры, ол контурдың құрамына кірмейтін тармақтарды қамтымайды.
5. Қорытынды: ең соңында бізде тармақтардағы белгісіз токтарға қатысты m-тәртіпті сызықты алгебралық теңдеулер жүйесі құрылады. Математика курсынан білетініміздей, бұндай теңдеулер жүйесінің тек бір ғана шешімі болады және оны түрлі әдіспен табуға болады. Мысалы: Гаусс, анықтауыштар, ауыстырулар.
Ескерктін жағдай, егер есепті шешу барысында тармақтағы токтың мәні теріс болып қалса, онда токтың дұрыс бағыты таңдап алынғанға қарама- қарсы және схемадағы токтың бағытын өзгерту міндетті емес.
1-ші суреттегі схемада тармақ саны m=6, түйін саны n=4, онда КТЗ бойынша n-1=4-1=3 теңдеуін, ал ККЗ бойынша m-n+1=6-4+1=3 теңдеуін құру керек.
1-суреттегі схемада тізбектегі барлық тармақтардан өтетін токтардың оң бағыты көрсетілген, олай болса, КТЗ блойынша алатынымыз төмендегідей:
- I2 + I4 + I6 = 0 (“a” түйіні)
I1 - I5 - I6 = 0 (“в” түйіні)
- I3 - I4 + I5 = 0 (“с” түйіні)
ККЗ бойынша теңдеу төмендегідей:
- (R1 + R01 ) I1 -(R3 + R03 ) I3 -R5 I5 = -E1 - E3 ,
- (R2 + R02 ) I2 + (R3 + R03 ) I3 - R4 I4 =- E2 +E3 ,
R4 I4 + R5 I5 - R6 I6 = 0.
Теңдеудің жазу тәртібіне көңіл аударсақ, онда бізде, әр қатардағы тармақтағы белгісіз токтар тармақтың тәртіп санының жоғарылауына сәйкес жазылады. Бұның мақсаты тізбектің электрлік күйінің теңдеуін матрицалық түрде жазуды оңайлату.
2.Контурлық ток әдісі.
Контурлық ток әдісі Кирхгоф заңдар әдісіне қарағанда тізбектің тізбектің электрлік күйінің теңдеу жүйесінің тәртібін қысқартуға мүмкіндік береді. Бұл әдіс контурлық токтар туралы түсінікке кіріспе ретінде негізделген.
Контурлық тоқтарға қатысты ККЗ негізінде (m-n+1) теңдеуі құрылады. Тізбектің электрлік күйі оңай әрі қолайлы болып құрылады, егер контурлық токтарды ұяшық контурлардың ішінде орналастырсақ, сондай-ақ контурлық токтардың бағыты 1-ші суретте көрсетілгендей сағат тіліне бағыттас түрде алынады. Теңдеуді жазған кезде, екі ұяшық- контурына да қатысты жалпы тармақтарға көңіл аудару керек. Жалпы тармақтар арқылы өтетін контурлық токтар байланысты деп аталады. Жалпы тармақтың резисторларында екі контурлық токтан түскен кернеуді ескерген жөн.
Контурлық токтарға байланысты ККЗ бойынша теңдеудің жазылу ережесінің белгілері келесі түрде:
1. Ұяшық контурының бағыты, негізгі контурдық бағытына сәйкес алынады, яғни сағат тіліне бағыттас.
2. Ұяшық контурына кіретін негізгі контурлық токтан түскен кернеуді барлық резисторлар үшін анықталады және қосу (+) таңбасымен жазылады.
3. Жалпы тармақтардағы байланысөан контур тогының бағыты негізгі ұяшық-контурлық тогының бағытына қарама- қарсы, сондықтан басты контур тогынан түскен кернеу алу (-) тақбасымен алынады.
4. Егер айналмалы контурдың бағыты және ЭҚК кернеу көзінің бағытымен сәйкес келсе, онда ЭҚК-тің таңбасы қосу (+) деп, ал керісінше жағдайда алу (-) деп алынады.
Элементтер ережесін ескере отырып, контурлық ток әдісі бойынша тізбектің электрлік күйінің теңдеуі 1- суреттегі схема үшін төмендегідей түрде болады:
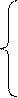(R1 + R01 + R3 + R03 + R5 ) IK1 - (R3 + R03 ) IK2 - R5 IK3 = - E1 -E3
- (R3+R03)IK1+(R2+R02+R3+R03+R4)IK2-R4IK3=E3-E2,
-R5 IK1 - R4 IK2 + (R4 + R5 + R6 ) IK3 = 0.
Сан мәндерін қоя отырып, алатынымыз:
17 IK1 - 5.8 IK2 – 2 IK3 = - 22,
-5.8 IK1 +13.2 IK2 – 3 IK3 = -26,
-2 IK1 – 3 IK2 + 10I K3 = 0.
Нәтижесінде бізде үш белгісіз контурлық тогы ьар 3-ші ретті сызықты алгебралық теңдеулер жүйесі шығады. Матрицалық түрде электр күйінің теңдеулер жүйесін көрсетейік.
[R] [I] = [E],
немесе жазып көрсетейік
17 -5.8 -2 IK1 -22
-5.8 13.2 -3 IK2 = -26
-2 -3 10 IK3 0,
 |  | |  |  | |
мұндағы: [I]- контурлық токтың баған матрицасы;
[E]-ЭҚК-тің контурының баған матрицасы;
[R]-кедергінің квадрат матрицасы.
Жазып көрсетілген матрицалық теңдеуден кқрініп тұр, бас диоганальға өатысты симметриалық болатын кедергілер матрицасы және тек қана бас диоганальға кіретін матрица элементтерінің шамасы оң болады. Ал қалғандарының барлығы теріс болады. Осы берілген кедергілер матрицасы контурлық ток әдісі мен тізбектің электрлік күйінің теңдеуінің дұрыстығын тексеру үшін қолданылады.
Матрицалық теңдеулердің шешімін анықтауыштардың(1-ші қолдану) көмегі арқылы Крамер әдісімен табамыз. Есептеулер едәір жеңілдетіледі, егер 3-ші ретті анықтауыштардың есептеуін микрокалькулятордың көмегімен жүргізсек(2-ші қолдану), онда алатынымыз:
 |  |  | | ||||
17 -5.8 -2 -22 -5.8 -2
Δ = -5.8 13.2 -3 = 1632.2 Δ 
= -26 13.2 -3
-2 -3 10 0 -3 10
= -4370
 |  |  | |||
17 -22 -2 17 -5.8 -22
Δ 
= -5.8 -26 -3 = -5724 Δ 
= -5.8 13.2 -26
-2 0 10 -2 -3 0
= -2591.2
Бұдан контурлық токтар тең болады:
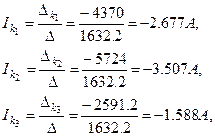
Тармақтың токтары контурлық токтардың алгебралық қосындысы ретінде ағымды тармақтар арқылы табылады. Келесі ереже қолданылады: егер контурлық токтың бағыты тармақтағы токпен бағыттас болса, онда берілген контурлық токтың мәні оң болады, ал бағыттары сәйкес келмесе, онда минус таңбасымен жазылады. Онда тармақтардың токтары тең болады.
I1 = - Ik1 = 2.677 A
I2 = - Ik2 = 3.507 A
I3 = Ik2 – Ik1 = - 0.83 A
I4 = Ik3 – Ik2 = 1.919 A
I5 = Ik3 – Ik1 = 1.089 A
I6 = - Ik3 = 1.588 A
3.Түйіндік кернеу әдісі.
Түйіндік кернеу әдісі де Кирхгоф заңдар әдісіне қарағанда тізбектің электрлік күйінің теңдеулер жүйесінің жазылу тәртібін азайтуға мүмкіндік береді. Контурлық ток әдісіне ұқсас түйіндік кернеу түсінігі енгізіледі, осы негізде КТЗ бойынша (n-1) электрлік теңдігінің теңдеуі құрылады. Кейбір жағдайларда түйіндік кернеу әдісі екі түйін әдісі болады, ол арасында активті және пассивті тармақтары қосылған екі түйінді электр тізбегін шешу үшін қолданылады.
Екі түйін әдісін 1 суреттегі схеманы есептеу кезінде қолдану үшін міндетті түрде электр тізбек бөлігінің эквиваленттік түрлендіруін орындау керек, соның ішінде R4, R5, R6 резисторларындағы кедергілер үшбұрышынан эквиваленттік кедергілер жұлдызшасына түрлендіруді жүргізу. Электрлік схемалар эквиваленттік деп аталады, егер
2 суретте кедергілер үшбұрышы және күшсәулелі кедергілер жұлдызшасы кәрсетілген. Олардың сәйкес эквивалеттік түрлендіруі кәп жағдайда схеманы қысқартуға мүмкіндік береді. Түрлендіру формулалары келесі түрде;
а)кедергілер үшбұрышын эквиваленттік кедергілер жұлдызшасына түрлендіру
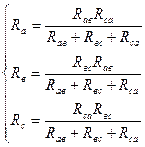
б)кедергілер жұлдызшасын эквиваленттік келергілер үшбұрышына түрлендіру
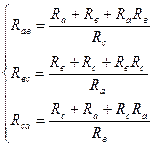
3 суретте кәрсетілгендей қажетті программаның эквиваленттік түрлендіруін жүргіземіз, мұндағы эквиваленттік кедергілер жұлдызшасының резисторларының параметрлері тең болады:
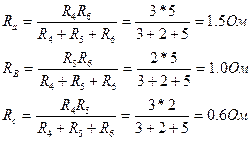
Ескере кетейік, 3 суреттегі схемада кернеудің нақты көздері орнын басу жүйелі схемасымен көрсетілген.
Екі түйін әдісінің негізгі мақсаты есептеу формуласымен түйіндік кернеу Udk деп аталады, түйіндердің арасындағы кернеу анықталады, ал содан кейін
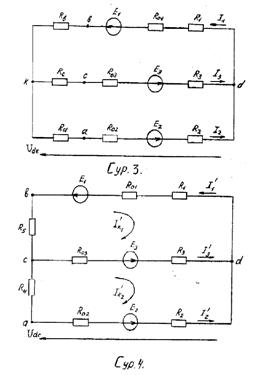
Ом заңы бойынша тармақтағы токтар есептеледі. Жалпы түрде түйіндік кернеу келесі формуламен анықталады:
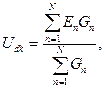
мұндағы Gn –тармақтың электр өтімділігі.
Түйіндік кернеуді есептеу кезіндегі белгілер ережесі келесідей: егер кейбір тармақтың түйіндік кернеудің бағыты және Э.Қ.К кейбір тармақтардағы кернеу көзінің бағыты бір-біріне қарама-қарсы болса, онда осы тармақтың En G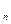 
туындысы қосу(+) таңбасымен жазылады және алу(-) таңбасымен кері жағдайда, бұл кезде тармақтағы токтың бағыты оң болсада. Егер тармақта кернеу көзі болмаса, онда берілген тармақтың Еn Gn туындысы 0-ге тең болады.
3 суреттегі схема үшін Udк түйіндік кернеу тең болады:
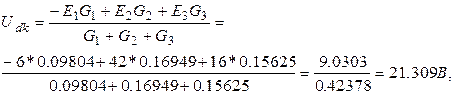
мұндағы:
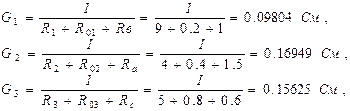
Тармақтағы токңтар Омның жинақталып қорытылған заңы
бойынша келесі қасиеттерге сәйкес анықталады:
- егер тармақтың тогының бағыты және кернеу көзінің ЭҚК
бағыттас болса, онда ЭҚК көзінің мәні қосу (+) таңбасымен, ал кері жағдайда алу (-) таңбасымен жазылады.
- егер тармақтың тогының бағыты және түйіндік кернеудің бағыты
бірдей болса, онда түйіндік кернеудің шамасы қосу (+) таңбасымен, ал кері жағдайда алу (-) таңбасымен алынады.
Тармақтағы токтар 3 суреттегі схемада тең болады:
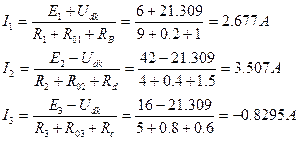
Тармақтардағы басқа токтардың мәнін анықтау үшін Ом заңы бойынша Uba түйіндік кернеудің шамасын табамыз:
Uba = Rb I1 + Ra I2 = 1 * 2.677 + 1.5 * 3.507 = 7.9375 B
Бұдан, R6 резисторы арқылы өтетін токтың мәні тең болады:
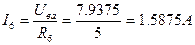
I4 және I5 токтарды басында құрған КТЗ теңдеуі бойынша да анықтауға болады:
I5 = I1 - I6 = 2.677 - 1.5875 = 1.0895 A
I4 = I5 - I3 = 1.0895 - (-0.8295) = 1.919 A
4.Эквивалентті генератор әдісі.
Эквивалентті генератор әдісін жалғыз, жеке тармақтағы кернеу мен токты анықтау үшін қолданған жөн. Бұл әдіс эквиваленттік генератор теориясынан шыққан (Тевенена теориясы), кез-келген сызықтық электр тізбегіне сәйкес келетін, екі екі жекеленген қысқыштарға қатысты қарастырылатын, Еэкв Э.Қ.К. мен кернеудің идеалды көзіне бір ізбен эквивалентті жалғанған, ол жеке қозғалыс режимінде осы қысқыштардың арасындағы кернеуге тең болады (яғни, осы қысқыштарға қосылған сыртқы тізбекті ажырату кезінде) және Rвх кедергісі бар идеалды резестивті элементке, ол барлық Э.Қ.К. 0-ге тең болғанда алынатын пассивті екі полюстің кірген кедергісіне тең.
Онда жекеленген пассивті тармақтағы ток тең болады:
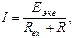
мұндағы, R-пассивті тармақтың резисторларының жалпы кедергісі.
1-суреттегі схема үшін эквивалентті генератор әдісіне сәйкес R6 резисторы арқылы өтетін ток келесі түрде анықталады:
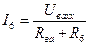
а) екі түйін әдісі:
Udc түйіндік кернеуін анықтаймыз:
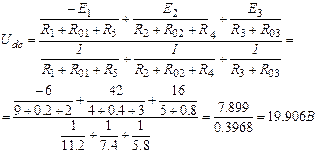
Тармақтағы токтарды табамыз:
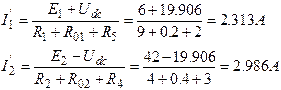
Бұдан алатынымыз
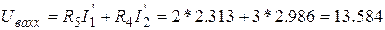
б) Контурлық ток әдісі:
Тізбектің электрлік күйінің теңдеулер жүйесін құрамыз:
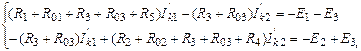
Параметрлердің мәнін қойғаннан кейін:
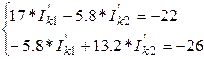
Шешуін Крамер әдісі бойынша табамыз (I қосымша):
Бұдан табатыныиыз:
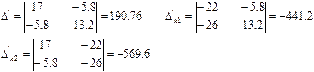
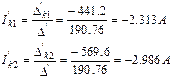
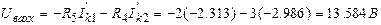
Екі жағдайда нәтижелері сәйкес келеді.
Идеалды кернеу көздері қысқартылған схема үшін (5 суреттің а)) Rbx кіру кедергісін есептеу үшін тізбектің эквивалентті түрлендіруін жүргізу қажет, бұл жағдайда екі вариант мүмкін.
1.R1, R3 , R5 резисторларынан тұратын кедергілер үшбұрышын, R13, R15, R35 резисторлары бар эквивалентті кедергілер жұлдызшасына түрлендіру (5 суреттің б)).
Эквивалентті жұлдызшаның резисторларының кедергісі тең болады:
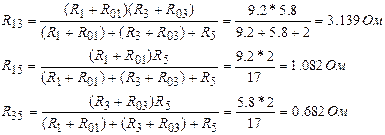
Тізбекке кірген кедергісін элементтерді кезектескен параллель қосу формуласы бойынша анықтаймыз:
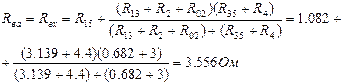
1.R3,R4 R5 резисторларынан тұратын кедергінің үшсәулелі жұлдызшасын, Rad, Rbd , Rba резисторлары бар кедергілердің эквивалентті үшбұрышына түрлендіру (5 сурет в)).
Эквивалентті үшбұрыш резисторларының кедергісі тең болады:
Тізбектің кірген кедергісін анологиялық түрде анықтаймыз:
Тізбектің кірген кедергісі екі жағдайдағы мәндері сәйкес келді. Бұдан 6 тармақтағы токтың соңғы мәнін аламыз.
Волтьметрдің көрсетуі және қуаттар балансы.
Идеалды вольтметр «д» және «с» түйіндері арасында қосылған, сондықтан вольтметрдің көрсетуі Ugс кернеуінің шамасына тең болады (1- сурет). Өлшеуіш прибор қосылған электр тізбегінің контурын бөліп көрсетейік, сонымен қатар ККЗ бойынша теңдеулер жүйесін құрайық (6- сурет):
а) «д,в,с» контуры
R01 I1 + R5 I5 – Ugc = E1
Бұдан алатыныз
Ugc = R01 I1 + R5 I5 – E1 = 0.2 * 2.677 + 2 * 1.089 – 6 =-3.287 B;
б) «g,d,c» контуры
R1 I1 + (R3 + R03) I3 + Ugc = E3
Бұдан алатынымыз
Ugc = E3 – R1 I1 – (R3 + R03) I3 = 16 –9 * 2.677 – 5.8 * (-0.83) =-3.279 B
Вольтметрдің көрсетулері жуықтап тең болады:
U = U» -3.3 B.
Қуаттар балансы жалпы энергия сақталу заңының тәсілі болып табылады, ол тізбектің электр күйінің дұрыс және дәл есептелгенің бағалау үшін қолданылады. Тұрақты ток тізбектері үшін қуаттар балансы келесі түрде болады: электр тізбегіндегі ЭҚК мен одан өткен токтардың көбейтіндісінің қосындысы тең болады, сол электр тізбегіндегі әрбір кедергідегі қуаттардың қосындысына тен болады:
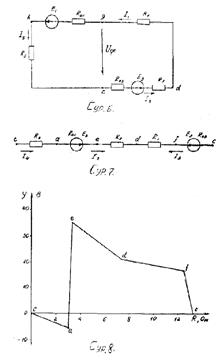
Қуаттар балансын құруда келесі ережелер қолданылады:
- электр энергиясын қабылдағыштардың қуаты әрқашан да оң шамалар;
- ЭҚК- нің бағытымен осы тармақтағы токтың оң бағыты сәйкес келсе, онда En In көбейтіндісі берілген тармақ үшін қосу(+) таңбасымен және кері жағдайда алу(-) таңбасымен алынады.
1- суреттегі схема үшін қуаттар теңдігі жазылады:
а) Энергия көздерінің қуаты:
Pкөз = E1 I1 + E2 I2 + E3 I3 = 6 * 2.677 + 42 * 3.507 + 16 * (- 0.83) = 150.076 Вт;
б) Энергия қабылдағыштардың қуаты:
Pқаб = (R1 + R01) I12 + (R2 + R02) I22 + (R3 + R03) I32 + R4 I42 + R5 I52 + R6 I62 =
9.2 * 2.677 + 4.4 * 3.507 + 5.8 * (-0.83) + 3 * 1.919 + 2 * 1.089 + 5 * 1.588 =
150.07 Вт.
Қуттар балансы дәлдіктің жоғары мәнімен сәйкес келді.
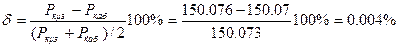
Инженерлік есептеулер үшін дәл есептеу қабылданады
δ ≤ I ÷3 %
