Эффективная часть спектра, которую нужно выделить полосовым фильтром, диапазон частот от 81,982 кГц до 118,018 кГц. Следовательно, эти частоты будут определять частоты границы полосы пропускания фильтра fп1 и fп2 соответственно. Граничную частоту полосы непропускания fз2 выбираем равной частоте первой гармоники спектра сигнала, находящейся после частоты (fн + 1/tи) = 125 кГц. Этой частотой является частота f3 = 127,027 кГц. Следовательно, fз2 = f3 = 127,027 кГц.
Найдем центральную частоту ПП:
кГц
Тогда граничная частота fз.1 полосы непропускания будет
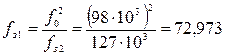кГц
Минимально-допустимое ослабление фильтра в ПН зависит от разницы амплитуд гармоник f3 и f5 спектра сигнала на выходе фильтра, выраженной в децибелах и заданной величиной Апол – полного ослабления:
дБ,
где
дБ
Таким образом, требования к полосовому фильтру сводятся к следующему:
кГц
кГц
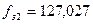кГц
кГц
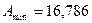дБ
дБ
Аппроксимация передаточной функции должна быть выполнена с помощью полинома Чебышева.
Формирование передаточной функции НЧ-прототипа
Находим граничные частоты ПП и ПН НЧ-прототипа.
кГц
кГц
По формулам получаем значения нормированных частот (wн)
Ωз 
Требования к НЧ-прототипу могут быть проиллюстрированы рисунком 3.
Рисунок 3. Требования к НЧ-прототипу
Находим коэффициент неравномерности ослабления фильтра в ПП из формулы:
А(Ω)=10lg[1+ε2ψ2(Ω)]
при A = ∆A и Ω = 1, когда ψ(1) = Тm(1) = 1:
Порядок фильтра Чебышева находится также из формулы А(Ω)=10lg[1+ε2ψ2(Ω)], но при A = Amin и Ω = Ωз, т. е. ослабление рассматривается в полосе непропускания. А в ПП полином Чебышева Тm(Ω) = ch(m archΩ), поэтому
Для вычисления функции arch х рекомендуется соотношение
По формуле вычисляем значение m. Расчетное значение m необходимо округлить в бóльшую сторону до целого числа. В данном примере принимает m = 3.
Пользуясь таблицей 2, находим полюсы нормированной передаточной функции НЧ-прототипа:
| ∆A, дБ | Порядок m=3 |
| 0,2 0,5 1,0 3,0 | -0,814634; -0,407317±j1,11701 -0,626457; -0,313228±j1,021928 -0,494171; -0,247085±j0,965999 -0,29862; -0,14931±j0,903813 |
Таблица 2.Полюсы нормированной передаточной функции НЧ-прототипа:
Формируем нормированную передаточную функцию НЧ-прототипа в виде
где v(р) – полином Гурвица, который можно записать через полюсы:
Производя вычисления, получим
Реализация LC-прототипа
Для получения схемы НЧ-прототипа воспользуемся методом Дарлингтона, когда для двусторонне нагруженного фильтра составляется выражение для входного сопротивления 
. Подставляя в формулу значение v(р) и значение h(p), получим
Данная формула описывает входное сопротивление двухполюсника. А если известно выражение для входного сопротивления, то можно построить схему двухполюсника, воспользовавшись, например, методом Кауэра. По этому методу формула для Zвх(р) разлагается в непрерывную дробь путем деления полинома числителя на полином знаменателя. При этом степень числителя должна быть больше степени знаменателя. Исходя из последнего, получим:
после чего производится ряд последовательных делений. Вначале числитель делим на знаменатель:
Затем первый делитель делим на первый остаток:
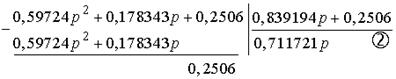
Второй делитель делим на второй остаток:
Третий делитель делим на третий остаток:
Получили четыре результата деления, которые отражают четыре нормированных по частоте и по сопротивлению элемента схемы в виде значений их проводимостей: pC, 1/pL, 1/R. Из анализа первого результата деления следует, что он отражает емкостную проводимость, поэтому все выражение можно записать в виде цепной дроби:
По данной формуле составляем схему (рисунок 4), на которой С1н = 3,349; L2н = 0,712; С3н = 3,349; Rг.н = Rн.н = Rнор.
Рисунок 4. Схема ФНЧ-прототипа
Денормируем элементы схемы НЧ-прототипа, используя соотношения:
где 
– нормирующая частота;
Rг – нормирующее сопротивление, равное внутреннему сопротивлению источника сигнала.
Используя соотношения и значения ωн и Rг получаем реальные значения элементов схемы НЧ-прототипа:
нФ
мГн
нФ
