ВВЕДЕНИЕ
Электрические фильтры – это линейные четырехполюсники, обладающие избирательными свойствами: они предназначены для выделения из состава сложного электрического колебания частотных составляющих определенного спектра частот, лежащего в полосе пропускания (ПП), и подавления тех составляющих, частоты которых лежат за пределами ПП, т. е. в полосе непропускания (ПН) или полосе задерживания (ПЗ). Между этими полосами находится переходная область.
Обычно выделяют следующие четыре типа фильтра:
- фильтр нижних частот (ФНЧ), пропускающий все частоты ниже выбранного значения wc и подавляющий высшие частоты
- фильтр верхних частот (ФВЧ), пропускающий все частоты выше выбранного значения и подавляющий нижние частоты
- режекторный или заграждающий фильтр, подавляющий выбранную полосу частот и пропускающий нижние и верхние частоты
- полосовой фильтр (ПФ), пропускающий выбранную полосу частот и подавляющий нижние и верхние частоты.
В соответствии с элементной базой можно выделить различные типы фильтров. Пассивные фильтры, содержащие элементы L и C. Они носят название LC-фильтры.
Требования микроминиатюризации аппаратуры заставили отказаться от использования индуктивностей, которые имеют большие габаритные размеры, особенно на низких частотах. Появились активные RC-фильтры, состоящие из резисторов, конденсаторов и активных приборов (например, транзисторов).
Расчет активного фильтра включает в себя два этапа – этап аппроксимации и этап реализации. На первом этапе по заданному максимальному и минимальному ослаблению в полосе пропускания и в полосе непропускания формируется передаточная функция фильтра, т.е. математическое описание цепи. На втором этапе создают схему цепи и определяют значение ее элементов по полученной передаточной функции.
РАСЧЕТ ПОЛОСОВОГО LC-ФИЛЬТРА
| Ти, мкс | Тн, мкс | tи | Um.н, В | Аmax,дБ | Апол,дБ | Rн, кОм |
| 40мкс |
На входе полосового фильтра действуют периодические радиоимпульсы (рисунок 1) с параметрами: период следования импульсов Tи = 111 мкс; длительность импульсов tи = 40 мкс; период несущей частоты Tн = 10 мкс; амплитуда колебаний несущей частоты Um.н = 15 В. Фильтр должен обеспечить максимально допустимое ослабление в полосе пропускания Аmax = ΔA = 3 дБ. Полное ослабление на границах полос непропускания Апол = 30 дБ. Сопротивления нагрузок фильтра слева и справа Rг =Rн = 1000 кОм. Характеристика фильтра аппроксимируется полиномом Чебышева.

Рисунок 1. Периодические радиоимпульсы, действующие на вход фильтра.
Расчет амплитудного спектра радиоимпульсов
Прежде чем приступать непосредственно к расчету фильтра, необходимо определить частотный состав сигнала, поступающего на вход фильтра, т. е. рассчитать и построить график амплитудного спектра периодических радиоимпульсов.
Вначале находится несущая частота:
 кГц.
кГц.
Затем рассчитывают частоты нулей огибающей спектра. Они зависят от длительности импульса:
 кГц
кГц
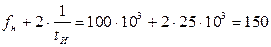 кГц
кГц
 кГц
кГц
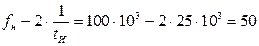 кГц
кГц
Максимальное значение огибающей в виде напряжения, соответствующее частоте fн, находится по формуле:

Зная максимальное значение и расположение нулей по оси частот, можно построить огибающую дискретного спектра периодических радиоимпульсов.
Внутри огибающей находятся спектральные составляющие или гармоники спектра с частотами fi, где i – номер гармоники. Они располагаются симметрично относительно несущей частоты, зависят от периода следования импульсов и находятся по формуле
 .
.
Учитывая, что
ƒи = 1/Ти = 1/(111*106 ) = 9,009 кГц
рассчитываем частоты гармоник, лежащих только справа от fн:
 кГц
кГц
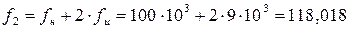 кГц
кГц
 кГц
кГц
 кГц
кГц  кГц
кГц
 кГц
кГц
Частоты гармоник, лежащих слева от fн, будут:
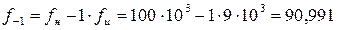 кГц
кГц
 кГц
кГц
 кГц
кГц
 кГц
кГц  кГц
кГц

Амплитуды напряжения i-ых гармоник находятся по формуле:
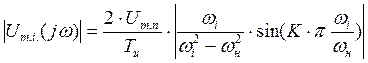
где K = tи/Tн – количество периодов несущих колебаний косинусоидальной формы в импульсе. В нашем примере К = 4.
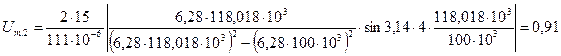 В
В
 В
В

|
Если скважность q, т.е. отношение периода следования импульсов Ти к длительности импульсов tи, равна целому числу, то в спектре отсутствуют гармоники с номерами, кратными скважности. Так как здесь q не равно целому числу, поэтому в спектре будут присутствовать 4,8,12 и т.д. гармоники слева и справа от несущей частоты. Поэтому спектр имеет вид (рисунок 2):
Рисунок 2. Модуль спектральной функции радиоимпульса






