Пусть к конденсатору преложено напряжение 
.
Мгновенные значения тока и напряжения в конденсаторе связывает формула 
Подставим в нее выражение и продифференцируем.
Угол сдвига фаз равен 
Вывод: в цепи с конденсатором ток опережает напряжение на угол 
Построим временную и векторную диаграммы для цепи с конденсатором.
Запишем отдельно выражение 
, отсюда 
, где обозначим 
-емкостное сопротивление
=Ом
Получаем закон Ома для максимальных и действующих значений в цепи с конденсатором.
Вывод: в цепи с конденсатором закон Ома справедлив для максимального и действующего значений, но не справедлив для мгновенных (
).
Построим зависимость 
, где 
Вывод: с ростом частоты емкостное сопротивление уменьшается, значит, конденсатор хорошо пропускает токи верхних и плохо токи нижних частот. Конденсатор-фильтр верхних частот.
Емкостное сопротивление равно бесконечности, значит вместо конденсатора на постоянном токе надо делать разрыв в цепи.
Энергетический процесс в цепи с конденсатором
Мгновенная мощность равна произведению мгновенного значения напряжения на мгновенное значение тока.
Первую и третью четверти периода напряжение и токимеют одинаковые знаки, конденсатор заряжается от источника и накапливает энергию электрического поля, мгновенная мощность положительна. Источник работает в режиме генератора. Вторую и четвертую четверти напряжение и ток имеют разные знаки, конденсатор разряжается, энергия возвращается обратно к источнику, мгновенная мощность отрицательна. Источник работает в режиме потребителя.
Вывод: в цепи с конденсатором источник и конденсатор обмениваются энергией и мерой этого обмена является реактивная мощность, которая обозначается 
.
- вар 
Пример решения задачи.
Дано:
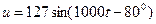
мкФ
Найти: 
, построить векторную диаграмму напряжения и тока
Ом
А
вар
Тестовые задания:
| Задание | Варианты ответов | ||
| 1.Зависит ли индуктивное сопротивление прямопропорционально от частоты? | Да; Нет. | ||
| 2.Какой из графиков соответствует зависимости емкостного сопротивления от частоты? | 
| ||
| 3.Справедлив ли закон Ома для мгновенных значений в индуктивных и емкостных цепях? | Да; Нет. | ||
| Задание | Электрическая цепь | Варианты ответов | |
| 4.Укажите соответствие векторной диаграммы в ответах и электрических цепей. | 1) цепь с «R»; 2) цепь с «L»; 3) цепь с «C». | 
| |
| 5.Укажите соответствие временной диаграммы в ответах и электрических цепей. | 1) цепь с «R»; 2) цепь с «L»; 3) цепь с «C». | 
| |
Последовательное соединение RL при гармоническом
Воздействии
В реальной катушке происходит 2 процесса: она нагревается и возникает ЭДС самоиндукции. Поэтому на схеме замещения реальную катушку изображает последовательное соединение R и L
-активная составляющая напряжения или в некоторых учебниках 
-резистивная составляющая напряжения.
- индуктивная составляющая напряжения
Пусть по цепи течет ток.
Напряжение на резисторе совпадает по фазе с током.
, где 
Напряжение на идеальной катушке опережает ток на угол 900.
, где 
Общее напряжение равно сумме напряжений участков (справедливо для мгновенных значений или векторов) 
Сложим напряжения участков векторно.
Из векторной диаграммы получаем 
и записываем уравнение напряжения на входе 
Вывод: при последовательном соединении R и L напряжение опережает ток на угол 
Закон Ома. Треугольники напряжений и сопротивлений.
Разделим все стороны диаграммы напряжений на 
. Получим треугольникнапряжений для действующих значений, из которого выведем закон Ома.
Откуда 
.
Обозначим 
- полное сопротивление цепи RL.
=Ом
Закон Ома для цепи RL
Разделим все стороны треугольника напряжений на токи получим треугольник сопротивлений
