Пример решения задачи
-первый закон Кирхгофа
- второй закон Кирхгофа
Составляем уравнения по законам Кирхгофа для данной схемы
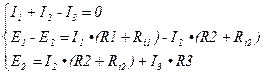
Пример решения задачи:
Дано:
E1 = 24 B
E2 = 18 B
Ri1 = 0, Ом
Ri2 = 0, Ом
R1 = 1,5Ом
R2 = 1,8Ом
R3 = 2 Ом
Найти: I1-3 -?
Подставляя исходные данные
Сокращаем коэффициенты в уравнениях
Выражаем I1 из первого уравнения и подставляем во второе
I1=I3-I2
3=I3-I2-I2=I3-2I2
Совместно записываем второе и третье уравнение и вычитаем почленно
3=I3-2I2
9=I3+I2
_-----------------------
-6=-3I2
I2=2A
Подставляем найденные I2=2A в третье уравнение
9= I2+I3=2+I3
I3=9-2=7A
Подставляем I2 и I3 в первое уравнение
I1= I3-I2 =7-2=5A
Ответы:
I1=5A
I2 =2A
I3=7A
Оба источника работают в режиме генератора, так как ток и ЭДС совпадают по направлению
Тестовые задания:
| Задание | Схема к заданию |
| 1.Составьте в общем виде необходимое количество уравнений по законам Кирхгофа. | 
|
МЕТОД КОНТУРНЫХ ТОКОВ
Этот метод позволяет уменьшать количество уравнений в системе.
Порядок расчёта:
1. Выбираем производное направление контурного тока;
2. Составляем уравнение по второму закону Кирхгофа для контурных токов. При записи учитываем падение напряжения от собственного контурного тока и контурных токов соседних контуров;
3. Решаем полученную систему уравнений и определяем контурные токи;
4. Рассчитываем действительные токи ветвей по правилу:
если в ветви течёт один контурный ток, то действительный ток равен этому контурному; если течет несколько, то действительный равен алгебраической сумме.
- второй закон Кирхгофа
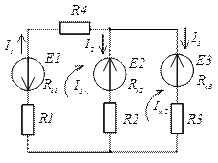
-E1 - E2 = I1к∙(R4 + Ri1 + R1 + Ri2 + R2) - I2к∙(R2 + Ri2)
E2 - E3 = I2к∙(R2 + Ri2 + R3 + Ri3) - I1к∙(R2 + Ri2)
Пусть при решении получилось
I1к=3A I2к=2A
Тогда I1 = I1к=3A и направлен вверх
I2 = I1к - I2к=3-2=1A и направлен вниз
I3 = I2к=2A и направлен вниз
Пример решения задачи
Дано:
E1 = 24 B
E2 = 18 B
Ri1 = 0,5 Ом
Ri2 = 0,2 Ом
R1 = 1,5 Ом
R2 = 1,8 Ом
R3 = 2 Ом
Найти: I1-3-?
30=6I1к 6=4∙5-2I2к
I1к=5A I2к=7A
_______________
I3=I2к=7A
I1= I1к=5A
I2= I2к- I1к=7-5=2A
Тестовые задания:
| Задание | Схема к заданию |
| 1.Составьте в общем виде необходимое количество уравнений по методу контурных токов. | 
|
МЕТОД ДВУХ УЗЛОВ
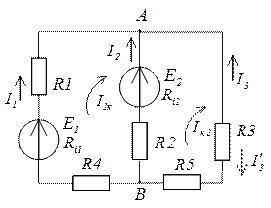
1.Обозначим узлы (А;В)
Под узлом А обозначим узел, к которому направлено больше ЭДС
2.Все токи направляем к узлу А
3. Рассчитываем проводимость каждой ветви по формуле единица разделить на сумму всех сопротивлений ветви.
G1= 
См
G2= 
См
G3= 
См
G4= 
См
4) Определяем напряжение между двумя узлами, в эту формулу Е входит со знаком "плюс" если она направлена к узлу А и со знаком "минус", если от узла
∙
5) Записываем токи ветвей
I1=(E1-UAB)∙G1
I2=(E1-UAB)∙G2
I3=(-E3-UAB)∙G3
I4=(-UAB)∙G4
6) Меняем направлен отрицательных токов (I3, I4)
Пример решения задачи
Дано:
E1=120 В
E8=128 В
Ri1=1 Ом
R1=10 Ом
R2=19 Ом
R3=40 Ом
R4=3 Ом
R5=20 Ом
Найти: I1-5=?
G1 
G2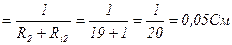 
G3 
UAB= 
I1=(E1-UАВ)∙G1=(120-108)∙ 
= 
= 
=0,8A
I2=(E2-UАВ)∙G2=(128-108)∙ 
=1A
I3=- UАВ∙G3 =(-108)∙ 
I3'=1,8A
Ответ:I1= Ii1=0,8A
I2=1A
I3=I5=1,8A
Тестовые задания:
| Задание | Схема к заданию |
| 1.Составьте в общем виде решение задачи по методу двух узлов. | 
|
