Эскиз требований к частотной характеристике аналогового ФНЧ-прототипа
представлен на рис.14. Переход от аналогового ФНЧ к цифровому невозможен без частоты дискретизации:
fд ≥ 2,3∙f2 =2,3∙6,495 ≈ 14,938
Произведём преобразование частоты для цифрового фильтра:
f1цп = fд/π ∙tg[(f1∙π)/ fд)] = 14,938/3,14∙tg[(3,94∙180)/ 14,938] = 5,185 кГц;
f2цп = fд/π ∙tg[(f2∙π)/ fд)] = 14,938/3,14∙tg[(6,495∙180)/ 14,938] = 22,882 кГц;

Рисунок 19 – Эскиз требований к частотной характеристике ЦФНЧ-прототипа
а) затухания;
б) коэффициента передачи.
Нормированная частота ЦФНЧ-прототипа:
Ω2цп = f2цп /f1цп ≈ 4,413.
Формула расчёта порядка цифрового фильтра Баттерворта имеет вид:
nб ≥ [A2 – 10 lg(100,1A1-1)]/(20lg Ω2цп)
Согласно исходным данным и рассчитанной нормированной частоте:
nб ≥ 4,28.
Округлив полученный результат до ближайшего целого числа, получим порядок фильтра Баттерворта для данного случая nб = 5.
Одним из вариантов синтеза цифровых фильтров является их синтез по известной АЧХ аналогового прототипа. Для такого синтеза необходимо знать требования к неравномерности АЧХ в полосе пропускания и ослабление в полосе задержки, а также граничные частоты ПП и ПЗ.
Для синтеза фильтра по его передаточной функции необходимо выбрать желаемую аппроксимацию и, исходя из неё, найти АЧХ фильтра.
Найдём С:
С = ε 2 =100,1A1 -1= 0,033.

Рисунок 20 – АЧХ ФНЧ в зависимости от Cn
Вычислим корни полинома Баттерворта для ФНЧ-прототипа 5-го порядка:
Рб1 =  = - 0,309 + j0,951,
= - 0,309 + j0,951,
Рб2 =  = - 0,809 + j0,588,
= - 0,809 + j0,588,
Рб3 =  = - 1,
= - 1,
Рб4 =  = - 0,809 - j0,588,
= - 0,809 - j0,588,
Рб5 =  =- 0,309 - j0,951
=- 0,309 - j0,951
Составим комплексно-сопряженные пары:
(Р – Рб1)(Р – Рб5) = Р2 + 0,618Р +1,
(Р – Рб3) = Р+1,
(Р – Рб2)(Р – Рб4) = Р2 + 1,618 Р +1,
Передаточная функция при С = 1 будет иметь вид:
Нб (р) = 
Передаточная функция при С ≠ 1 будет иметь вид:
Нб (р) =  .
.
где δ для данного варианта равна:
δ = 2n √(1/С) = 12 √(1/0,033) = 1,408.
Следовательно:
Нб (р) =  .
.
Далее к каждому сомножителю применим билинейное z-преобразование, предварительно выполнив нормирование относительно граничной частоты ПП:

где ω = 2πf1цп=2∙3,14∙5,185 = 32,577
 , а
, а  .
.
Для удобства вычислений введём замену:
x = (1 – z -1); x2 = (1 - 2 z -1 + z -2);
y = (1 + z -1); y2 =(1 + 2 z -1 + z -2);
xy = (1 – z -2).Посчитаем передаточную функцию используя замену:
Нб (р) =  .=
.=
=  .=
.=
=  =
=  =
=
=  =
=
=  =
=
=  ∙
∙  ∙
∙  =
=
=  =
=
= 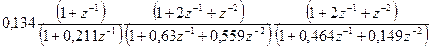 =.
=.
Окончательный вариант передаточной функции имеет вид:
Нб (z) =  .
.
Разложим данную функцию на три подфункции и запишем соответствующие разностные уравнения:
Нб1(z) =  ;
;
Y(z) = 0,134X(z) +0,134 z -1 X(z) - 0,211z -1 ;
y(n) = 0,134x(n) +0,134 x(n-1) - 0,211y(n-1);
Нб2(z) =  ;
;
Y(z) = X(z) +2 z -1 X(z) + z -2 X(z) - 0,63 z -1 Y(z) -0,559 z -2 Y(z);
y(n) = x(n) +2 x(n-1) + x(n-2) - 0,63 y(n-1) -0,559 y(n-2);
Нб3(z) =  ;
;
Y(z) = X(z) +2 z -1 X(z) + z -2 X(z) - 0,464 z -1 Y(z) +0,149 z -2 Y(z);
y(n) = x(n) +2 x(n-1) + x(n-2) - 0,464 y(n-1) +0,149 y(n-2);

Рисунок 22 – Схема ЦФНЧ Баттерворта 6-го порядка во временной области

Рисунок 23 – Схема ЦФНЧ Баттерворта 6-го в каноническом виде
Приведём передаточную функцию Баттерворта к классическому виду. В результате получим:
Нб (z) =  =
=
= 
Произведём замену z = ejΩn :
Нб (ejΩ) =  =
=
= 
 .
.
Введём замену:
A = 0,134[1+5cos(Ω) + 10cos(2Ω) + 10cos(3Ω) +5cos(4Ω) + 1cos(5Ω)];
B = 0,134 [-5sin(Ω) - 10sin(2Ω) -10sin(3Ω) - 5sin(4Ω) - 1sin(5Ω)];
D = 1 + 1,305 cos(Ω)+1,231 cos(2Ω) + 0,797 cos(3Ω) + 0,183 cos(4Ω) + 0,052 cos(5Ω);
F = -1,305sin(Ω) – 1,231sin(2Ω) – 0,797sin(3Ω) – 0,183sin(4Ω) – 0,052sin(5Ω).
Произведя расчёты частоты и коэффициентов A, B, D, F в MathCad, получим:
Ω = 2πf1/fд = (2∙180∙ 3,94)/14,938 = 94,952
A=-0,157; B=0,528; D=0,429; F= - 0,487;
Н(Ω) =  = 0,849.
= 0,849.
θ(Ω)=arctg(A/B) – arctg(D/F) = -0,433 рад. – при условии что угол находится в диапазоне
от –π/2 до π/2.
При использовании диапазона измерения углов от –π до π:
X=π/2+arctg(B/A)=0,289;
Y=arctg(F/D)=-0,849
θ(Ω)=x-y=1,138
Вывод: В данной части курсовой работы мы изучили принцип перехода от аналогового фильтра к цифровому на основе z-преобразования.
Н(Ω)≈ H(f)
Это значит, что синтез фильтра произведён верно.






