4.1 Цель работы
Целью работы является экспериментальная проверка законов Ома и Кирхгофа для разветвленных цепей переменного тока, построение векторных и топографических диаграмм.
4.2 Подготовка к работе
4.2.1 Повторить раздел курса ТЭЦ «Линейные электрические цепи однофазного синусоидального тока».
4.2.2 Рассчитать реактивные проводимости  ,
,  , активные проводимости q1 и q2, комплексные Y1, Y2 проводимости, модули комплексных проводимостей (полные проводимости) y1, y2, аргументы комплексных проводимостей (углы сдвига фаз между напряжением и токами I1, I2)
, активные проводимости q1 и q2, комплексные Y1, Y2 проводимости, модули комплексных проводимостей (полные проводимости) y1, y2, аргументы комплексных проводимостей (углы сдвига фаз между напряжением и токами I1, I2) 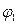 ,
,  для каждой ветви, входную комплексную Y проводимость, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи)
для каждой ветви, входную комплексную Y проводимость, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи) 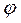 (рисунок 4.1), согласно заданному варианту (таблица 4.1). Результаты расчета занести в таблицу 4.2.1 и 4.2.2.
(рисунок 4.1), согласно заданному варианту (таблица 4.1). Результаты расчета занести в таблицу 4.2.1 и 4.2.2.
4.2.3 Рассчитать, согласно заданному варианту (таблица 4.1), емкостную проводимость  , индуктивную проводимость
, индуктивную проводимость  , активную проводимость q1, входную комплексную проводимость Y, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи)
, активную проводимость q1, входную комплексную проводимость Y, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи) 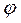 (рисунок 4.2), Результаты расчета занести в таблицу 4.3.
(рисунок 4.2), Результаты расчета занести в таблицу 4.3.
4.2.4 Рассчитать комплексные и действующие значения токов и напряжений на каждом элементе схем (рисунок 4.1) по параметрам своего варианта (таблица 4.1). Результаты занести в таблицу 4.4.
4.2.5 Рассчитать комплексные и действующие значения токов в каждой ветви схемы (рисунок 4.2) по параметрам своего варианта (таблица 4.1). Результаты занести в таблицы 4.5.
4.2.6 Рассчитать активную, реактивную и полную мощности для схемы (рисунок 4.1). Результаты занести в таблицу 4.4. Построить треугольник мощностей.
4.2.7 Рассчитать активную, реактивную и полную мощности для схемы (рисунок 4.2). Результаты занести в таблицу 4.5.
4.2.8 Построить по результатам расчётов векторные диаграммы токов и напряжений для схемы (рисунок 4.1).
4.2.9 Построить по результатам расчётов векторные диаграммы токов, треугольник токов для схемы (рисунок 4.2).
4.2.10 Построить по результатам расчетов треугольники проводимостей и мощностей для схемы (рисунок 4.2).
Таблица 4.1
| № варианта | ||||||
| R1, Ом | ||||||
| R2, Ом | ||||||
| С, мкФ | 0,1 | 0,08 | 0,1 | 0,3 | 0,05 | 0,2 |
| L, мГн | ||||||
| f, кГц | ||||||
| U, В |
4.3 Порядок выполнения работы
4.3.1 Собрать цепь по схеме (рисунок 4.1). Установить параметры цепи согласно заданному варианту (таблица 4.1).
4.3.2 Измерить токи в каждой ветви и напряжения на каждом элементе. Результаты занести в таблицу 4.4.
Таблица 4.2.1
| Вид исследований | R1, Ом | R2, Ом | С, мкФ | L, мГ | f, кГц | bC, См | bL, См | q1, См | q2, См |
| Теоретический расчет | |||||||||
| Эксперимент |
Таблица 4.2.2
| Вид исследований | y  , См , См
| 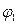 , град. , град.
| y2, См |  , град. , град.
| y, См | 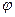 , град. , град.
|
| Теоретический расчет | ||||||
| Эксперимент |
Таблица 4.3
| Вид исследований | R1, Ом | С, мкФ | L, мГ | f, Гц | bC, См | bL, См | q1, См | b, См | y, См | Y, См |  ,
град ,
град
|
| Теоретический расчет | |||||||||||
| Эксперимент |
Таблица 4.4
| U, B | UR1 В | UR2, В | UL, В | Uc, В | I, мA | I1, мA | I2, мA | P, Вт | Q, Вар | S, ВА | |
| Теоретический расчет | |||||||||||
| Эксперимент |
Таблица 4.5
| Вид исследований | U, B | I, мА | I  ,
мA ,
мA
| I  ,
мA ,
мA
| I 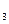 ,
мA ,
мA
| P, Вт | Q, Вар | S, ВА |
| Теоретический расчет | ||||||||
| Эксперимент |
4.3.3 Собрать цепь по схеме (рисунок 4.2). Установить параметры цепи согласно заданному варианту (таблица 4.1).
4.3.4 Измерить токи в каждой ветви и напряжение на входе цепи. Результаты занести в таблицу 4.5.

Рисунок 4.1
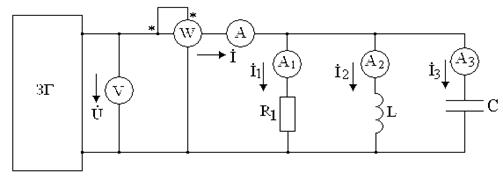
Рисунок 4.2
4.4 Обработка результатов экспериментов
4.4.1 Для схемы (рисунок 4.1) по результатам экспериментов построить векторные диаграммы токов и напряжений.
4.4.2 Для схемы (рисунок 4.1) рассчитать по данным эксперимента реактивные проводимости  ,
,  , активные проводимости q1 и q2, комплексные Y1, Y2 проводимости, модули комплексных проводимостей (полные проводимости) y1, y2, аргументы комплексных проводимостей (углы сдвига фаз между напряжением и токами)
, активные проводимости q1 и q2, комплексные Y1, Y2 проводимости, модули комплексных проводимостей (полные проводимости) y1, y2, аргументы комплексных проводимостей (углы сдвига фаз между напряжением и токами) 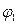 ,
,  для каждой ветви, входную комплексную Y проводимость, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи)
для каждой ветви, входную комплексную Y проводимость, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи)  . Результаты записать в таблицы 4.2.1 и 4.2.2.
. Результаты записать в таблицы 4.2.1 и 4.2.2.
4.4.3 Для схемы (рисунок 4.1) проверить законы Кирхгофа. Определить сos j, активную Р, реактивную Q и полную S мощности цепи. Результаты занести в таблицу 4.4. Проверить соотношения, связывающие эти мощности. Построить треугольник мощностей.
4.4.4 Для схемы (рисунок 4.2) по результатам экспериментов построить в масштабе векторную диаграмму токов и треугольник токов.
4.4.5 Для схемы (рисунок 4.2) определить по результатам эксперимента емкостную проводимость  , индуктивную проводимость
, индуктивную проводимость  , активную проводимость q1, входную комплексную Y проводимость, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи)
, активную проводимость q1, входную комплексную Y проводимость, модуль входной комплексной проводимости (полную проводимость) y, аргумент входной комплексной проводимости (угол сдвига фаз между напряжением и током на входе цепи)  . Результаты записать в таблицу 4.3. Построить треугольник проводимостей.
. Результаты записать в таблицу 4.3. Построить треугольник проводимостей.
4.4.6 Для схемы (рисунок 4.2) проверить первый закон Кирхгофа по результам эксперимента.
4.4.7 Определить сos j, активную Р, реактивную Q и полную S мощности цепи. Результаты записать в таблицу 4.5. Проверить соотношения, связывающие эти мощности. Построить треугольник мощностей.
4.5 Методические указания
4.5.1 Для электрической цепи (рисунок 4.1) комплексные проводимости ветвей рассчитываются по формулам

где  ;
;  ;
;
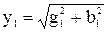 ;
;  ;
;

где  ;
;  ,
,
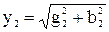 ;
;  .
.
Входная комплексная проводимость равна

где  ;
;
 ;
;  ;
;  .
.
Ток в каждой ветви равен 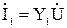 ,
,  .
.
Ток на входе цепи 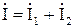 можно представить в виде
можно представить в виде

где 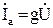 -активная составляющая тока, совпадающая по фазе с напряжением;
-активная составляющая тока, совпадающая по фазе с напряжением;
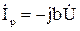 - реактивная составляющая тока, сдвинутая по фазе относительно напряжения на угол
- реактивная составляющая тока, сдвинутая по фазе относительно напряжения на угол  (рисунок 4.3).
(рисунок 4.3).

Рисунок 4.3
Треугольники токов и проводимостей при активно-емкостном характере цепи представлены на рисунках 4.4 а) и 4.4 б).


а) б)
Рисунок 4.4
По экспериментальным данным полные проводимости ветвей и полная входная проводимость определяются по формулам
 ,
,  ,
,  .
.
Аргументы комплексных проводимостей ветвей равны
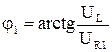 ,
,  .
.
Аргумент входной комплексной проводимости (разность фаз напряжения и тока на входе цепи) можно определить из векторной диаграммы, построенной по экспериментальным данным.
Активные и реактивные проводимости определяются по формулам
 ,
,  ,
, 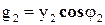 ,
, 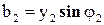 ,
,
 ,
,  .
.
Первый закон Кирхгофа можно проверить по векторной диаграмме. Второй закон Кирхгофа проверяется по формулам
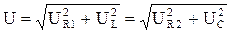 .
.
4.5.2 Для электрической цепи (рисунок 4.2) комплексные проводимости ветвей равны:
 ,
,  ,
, 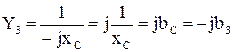
где  ,
,  .
.
Комплексная входная проводимость равна
 .
.
По эксперементальным данным
 ,
,  ,
,  ,
,  ,
, 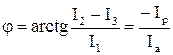
где  - активная составляющая тока
- активная составляющая тока 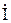 ;
;
 - реактивная составляющая тока
- реактивная составляющая тока 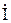 ;
;
 . Модуль реактивной составляющей тока равен
. Модуль реактивной составляющей тока равен  .
.
Векторная диаграмма представлена на рисунке 4.5, треугольники токов и проводимостей на рисунках 4.4 а), 4.4 б).
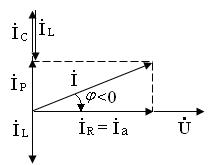
Рисунок 4.5
Активная, реактивная и полная мощности для схем (рисунки 4.1,4.2) определяются по формулам
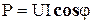 ,
,  ,
,  .
.
Треугольники мощностей приведены на рисунках 4.6 а)- цепь имеет активно-индуктивный характер, 4.6 б)- цепь имеет активно-емкостной характер.


а) б)
Рисунок 4.6






