Время жизни квантовомеханической системы в квазистационарном состоянии не может быть бесконечно долгим. Поэтому волновая функция ψ такого состояния с энергией En зависит от времени:
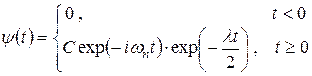(З.1)
(где частота ωn = En / ћ), причем временной множитель функции при t > 0 содержит не только мнимую, но и действительную экспоненту. Так как квадрат модуля волновой функции есть вероятность найти частицу «внутри системы», то
,
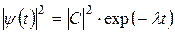что соответствует экспоненциальному затуханию вероятности со временем (в соответствии с основным законом радиоактивного распада).
Рассмотрим для конкретности переход системы из возбужденного состояния в основное, сопровождающийся электромагнитным излучением. Каков будет спектр испускаемого излучения I (E)? Чтобы ответить на этот вопрос, разложим функцию (З.1) в интеграл Фурье[209] по частотам непрерывного спектра ω = E / ћ:
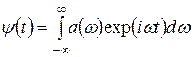, (З.2)
где
. (З.3)
Так как функция ψ = 0 при t < 0, после подстановки (З.1) в (З.3) в результате интегрирования получаем:
. (З.4)
Как известно электродинамики, при излучении электромагнитных волн системой зарядов, совершающей гармонические колебания с частотой ω, энергия излучения пропорциональна квадрату амплитуды этих колебаний. С квантовой точки зрения это означает, что вероятность испускания фотона с энергией Е = ћω пропорциональна квадрату модуля амплитуды соответствующего коэффициента разложения волновой функции (З.1) по спектру частот:
. (З.5)
Из (З.5) следует, что интенсивность излучения достигает максимума при ω = ωn. Обозначив эту максимальную интенсивность как
и, переходя от частот к энергиям и к ширине уровня Г = ћλ, находим, что
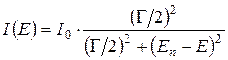. (З.6)
Таким образом, энергетический спектр излучения при экспоненциальном законе распада возбужденного состояния имеет форму кривой Лоренца с центром в точке Е = Еn и шириной на половине высоты равной Г.
Процесс, обратный испусканию, – резонансное поглощение – описывается той же зависимостью. Это значит, что сечение поглощения имеет вид
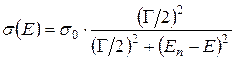, (З.7)
где σ 0 – максимальное сечение, определяемое физикой процесса. Формулы вида (З.7) в ядерной физике называют формулами Брейта-Вигнера. Для взаимодействия бесспиновых частиц,[210] относительный орбитальный момент которых равен нулю,
, (З.8)
где 
– длина волны налетающей частицы a, Т – ее кинетическая энергия, Г a – ширина уровня при испускании налетающей частицы (упругое рассеяние); Г b – при испускании другой частицы b (реакция, или неупругий процесс); Г = Г a + Г b – полная ширина. В случае резонанса сечение упругого рассеяния
,
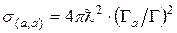Это означает, что,если энергетически возможно только упругое рассеяние (Г b = 0), то максимальное сечение (в резонансе) равно
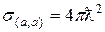. (З.9)
Найдем, при каких условиях максимально сечение реакции. Для этого продифференцируем выражение (З.8) по Г b при условиях Т = En и Г = Г a + Г b.
,
откуда следует, что сечение реакции максимально при Г a = Г b и равно
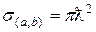. (З.10)
Таким образом, резонансные сечения упругого и неупругого процессов ограничены значениями (З.9) и (З.10). Кроме того, существует и ограничение и для полного сечения σ = σ ( a , a ) + σ ( a , b ):
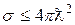. (З.11)
Из соотношений (З.9-З.11) следует, что упругое рассеяние возможно в отсутствие неупругих процессов (реакций), но не наоборот: неупругий процесс при любых условиях сопровождается упругим рассеянием.
