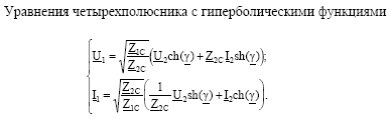
Расчет первичных параметров четырехполюсников по его принципиальной схеме
Первичные параметры любой схемы можно определить, применяя метод узловых напряжений или метод контурных токов.
Пусть задан четырёхполюсник, содержащий n независимых узлов.
Подключим на вход источник тока J 1 и на выход J 2, которые определяют входной ток I 1 и выходной ток I 2. Внутри нет независимых источников.
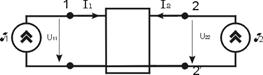
Тогда можно составить систему уравнений методом узловых напряжений, и записать ее в матричной форме:
J 1 = I 1, J 2 = I 2, U 11 = U 1, U 22 = U 2
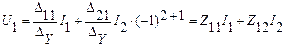
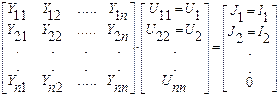Решая систему относительно напряжений U 11 и U 22, получим уравнения в системе Z– параметров.
 |
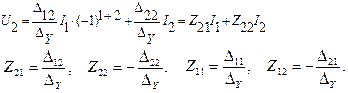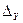– общий определитель [Y]– матрицы.
Таким образом, метод узловых напряжений позволяет определить Z параметры.
Аналогично, методом контурных токов можно рассчитать Y параметры.
Составные четырехполюсники
Составными называются четырёхполюсники, составленные из простых, соединённых между собой определенным способом.
Различают пять способов соединения четырёхполюсников.
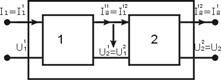
1) Каскадное соединение. Выходные полюса предыдущего соединяются с входными полюсами последующего четырехполюсника.
Электрическое состояние при каскадном соединении:
 |
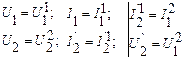Вопрос: Как определить первичные параметры составного четырёхполюсника, если известны первичные параметры его частей?
 |
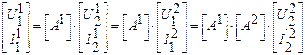
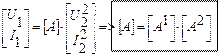При каскадном соединении перемножаются A матрицы.
2) Последовательное соединение четырехполюсников – входные полюса соединены между собой последовательно и выходные – также.
Если положительные направления токов при соединении четырехполюсников не меняются, то такое соединение называется регулярным, если нет – то нерегулярным.
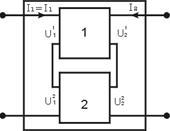
U1 = U1 1 + U1 2, U2 = U2 1 + U2 2
I 1 = I 11 = I 12, I 2 = I 21 = I 22.
– 
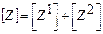формула расчёта параметров составного четырёхполюсника.
При последовательном соединении четырёхполюсников складывается [Z]– матрицы.
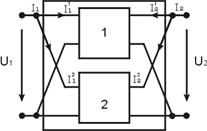
3). Параллельное соединение четырехполюсников - четырёхполюсников – входные полюса между собой соединены параллельно и выходные также.
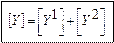U 1 = U11 =U12, U 2 = U21 =U22.
I 1 = I 11 + I 12, I 2 = I 21 + I 22.
– формула расчёта параметров составного четырёхполюсника.
При параллельном соединении четырёхполюсников складывается [Y]– матрицы.
4) Последовательно-параллельное соединение – входные полюса соединены последовательно, а выходные – параллельно.
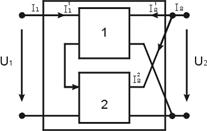
При последовательно-параллельном соединении складываются [H]– матрицы.
 |
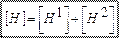5) Параллельно-последовательное соединение – входные полюса соединены параллельно, выходные – последовательно. При таком соединении складываются [F]– матрицы.
 |
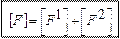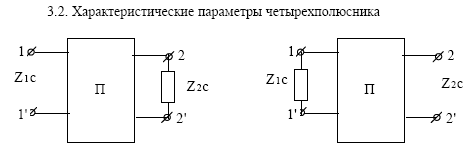
Характеристические параметры четырёхполюсника – это такие параметры, которые характеризуют какие-то особые свойства четырёхполюсника.
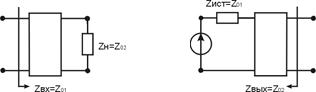
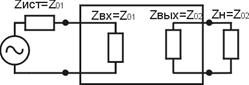
I) Характеристические сопротивления Z 01(jω), Z 02(jω), – это численные значения сопротивлений. Если на входе или на выходе четырехполюсника включить резисторы с сопротивлениями, равными характеристическим значениям, то четырёхполюсник приобретает определённые, характерные свойства.
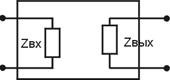
1) Если ZН = Z02, то Zвх = Z01;
2) 2) Если Zист = Z01, то Zвых = Z02;
Если выполняются 1) и 2) условия, то такой режим работы называется согласованным режимом четырёхполюсника по входу и выходу. Он характеризуется передачей максимальной мощности от источника в нагрузку.
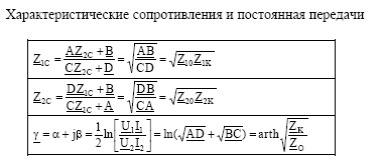
Характеристические сопротивления можно рассчитать, пользуясь первичными параметрами.
Например, в системе A параметра:
 |
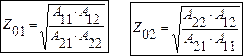Если четырёхполюсник обладает одинаковыми параметрами A11 = A22, то тогда характеристические сопротивления равны
 |
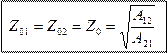Такие четырехполюсники называются симметричными.
2) Коэффициент трансформации.
Для количественной оценки свойства трансформации сопротивления вводят этот параметр:
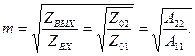
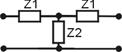
Если у четырёхполюсника A11=A22, то m = 1 и четырёхполюсник называется симметричным, т.к. Zвх = Zвых, Z01 = Z02.
3) Характеристическая постоянная передачи
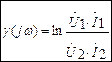Г(jω), γ(jω).
Чтобы понять физический смысл этого параметра, представим его в алгебраической форме: γ(jω)= A + j B
 |
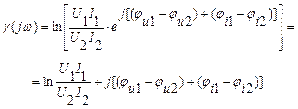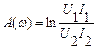
– постоянная затухания или коэффициент затухания (измеряется в Белах [Б]) или децибелах [дБ]
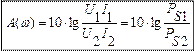где P S1 – полная мощность на входе,
P S2 – полная мощность на выходе.
Постоянную затухания можно выразить через токи и напряжения в четырёхполюсниках. Если U 1 = I 1∙ Z 0, U 2 = I 2∙ Z 0, то
[дБ]
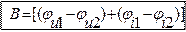
– коэффициент фазы.
Полезно запомнить, что уменьшению мощности в 2 раза (уменьшению напряжения или тока в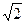 
раз) соответствует A дБ ≈ 3 дБ, уменьшению мощности в 10 раз – A дБ ≈ 10 дБ, уменьшению напряжения в 10 раз – A дБ ≈ 20 дБ,
Постоянная фазы B характеризует изменение начальной фазы напряжения или тока пи передачи энергии от источника к нагрузке. Эту величину выражают в угловых единицах – радианах или градусах.
