До першої групи відносяться перетворювачі кодів, що синтезуються як звичайні комбінаційні схеми на логічних елементах І, АБО, І-НЕ, АБО-НЕ та ін.
Другу і третю групу складають перетворювачі кодів, побудовані за блоковими схемами: дешифратор - шифратор, дешифратор - матриця запам'ятовуючого пристрою.
Четверту групу утворюють перетворювачі кодів, які реалізуються на основі програмованих логічних матриць. На рис.2 зображено умовні графічні позначення перетворювачів кодів.
У загальному вигляді в основному полі прямокутника міститься позначення Х/У (рис. 2, а). Букви X, У можуть бути замінені позначеннями інформації, присутньої відповідно на входах і виходах. Наприклад, на рис. 2,б зображено перетворювач двійкового коду в десятковий (В - від англ. binary - двійковий, DEC - від англ. decimal - десятковий), а на рис. 2,в. Перетворювач коду Грея у двійковий код.
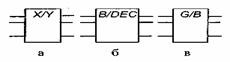
Рис. 2.
Побудова перетворювачів кодів здійснюється відповідно до загальної методики синтезу комбінаційних дискретних пристроїв, яка включає три основних етапи:
1. Одержання таблиці відповідності, яка реалізується перетворювачем кодів.
2. Одержання і перетворення (мінімізація) логічних функцій, що описують синтезований перетворювач кодів.
3. Синтез функціональної та принципової електричних схем.
Реалізація другого і третього етапів синтезу перетворювачів кодів істотно залежить від вибраного принципу побудови і заданої елементної бази. Розглянемо декілька прикладів побудови різних перетворювачів кодів.
Приклад 1. Побудувати схему асинхронного перетворювача двійкового коду 8421 у код 2421 на інтегральних логічних елементах КР1533ЛРЗ, КР1533ЛН1.
Код 2421 використовується при побудові обчислювальних пристроїв, які обробляють інформацію у двійково-десятковій системі числення. Кожні чотири розряди цього коду служать для відображення одного десяткового розряду згідно з табл. 1, де х4, х3, х2, х1 - розряди двійкового коду з вагою 8421, а у4, у3, у2, у1 - розряди двійкового коду з вагою 2421.
Аналіз табл.1 показує, що синтезована схема перетворювача являє собою дискретний пристрій з чотирма входами і виходами. Значення виходів пристрою визначені тільки на 10 наборах з 16, решта (6 наборів) можуть бути віднесені до умовних, тому що вони не зустрічаються при роботі пристрою. Синтезована схема перетворювача описується системою логічних функцій.
Таблиця 1.
| Після розв’язання задачі мінімізації одержимо такі типові ДНФ функції:
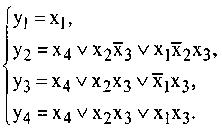На рис.3 наведено функціональну схему синтезованого перетворювача, який містить 3 елементи І- АБО - НЕ (3 корпуси) КР1533ЛР11 і 6 елементів НЕ (1 корпус) КР1533ЛН1.
|
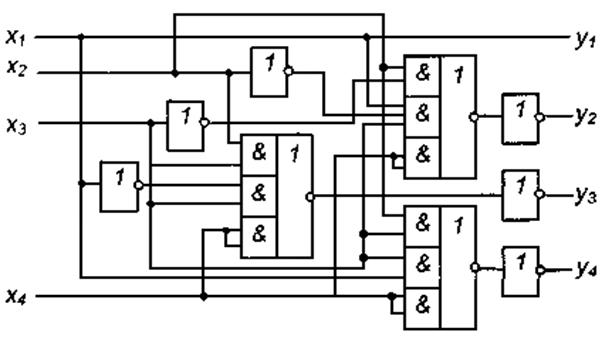
Рис. 3.
Тема для самостійного опрацювання (Лекція №11с):
Перетворювач двійкового коду в семи сегментний для цифрової індикації
Зробити стислий конспект, обов’язково замалювати схеми та переписати приклади.
